1 Induktiivinen päättely
1.1 Johdanto
Yksi parhaista yleispätevistä ongelmanratkaisuohjeista on ”tutki pieniä tapauksia”. Hyödyllisyys perustuu siihen, että pienempien tapauksien kautta saadaan ymmärrystä isommista tapauksista. Induktiivinen päättely pyörii tämän ajatuksen ympärillä. Ideana on, että tutkimalla pieniä tapauksia ja miten tapauksesta päästään ”yhtä isompaan” tapaukseen saadaan ymmärrystä myös isommista tapauksista. Käymme läpi neljä esimerkkiä, jotka demonstroivat tätä ideaa erilaisissa ympäristöissä.
1.2 Esimerkki 1: Kävelyreitit
Vaihtoehtoja on todella monta, joten ei ole järkevää käydä niitä kaikkia yksitellen läpi. Voimme kuitenkin tutkia pieniä tapauksia eli lähellä olevia ruutuja ja miettiä, kuinka monella tavalla niihin voidaan päästä. Näitä arvoja on kohtalaisen helppo laskea, koska tapoja on paljon vähemmän.
Taulukoinnin kautta keksitään tehtävän avainidea: se, monellako tavalla ruutuun voi päästä, on sen alapuolella ja vasemmalla puolella olevien ruutujen lukujen summa. Jos nimittäin haluamme päästä ruutuun \((x, y)\), tulee meidän sitä ennen päästä joko ruutuun \((x-1, y)\) tai \((x, y-1)\).
Nyt taulukointia on helppo jatkaa edeten vasemmasta alanurkasta kohti oikeaa ylänurkkaa. Saamme täytettyä ruudukon:
Vastaus tehtävään on täten \(252\).
1.3 Esimerkki 2: Summa
Toisin sanoen meitä pyydetään todistamaan suora kaava ensimmäisen \(n\) luvun summalle. Esimerkiksi \[1 + 2 + 3 + \ldots + 100 = \frac{100 \cdot 101}{2} = 50 \cdot 101 = 5050.\]
Huomataan, että väite pätee ainakin pienillä arvoilla: \[\begin{eqnarray} 1 &=& \frac{1 \cdot 2}{2}, \\ 1 + 2 = 3 &=& \frac{2 \cdot 3}{2}, \\ 1 + 2 + 3 = 6 &=& \frac{3 \cdot 4}{2}, \\ 1 + 2 + 3 + 4 = 10 &=& \frac{4 \cdot 5}{2}. \\ \end{eqnarray}\]
Päteekö väite myös suurilla arvoilla? Tätä varten esitetään toinen kysymys, joka on kriittinen ratkaisun kannalta:
Vastaus. Sekä vasen että oikea puoli kasvaa \(n+1\) verran.
Vastauksen perustelu. Vasen puoli tietysti kasvaa \(n+1\) verran: vasen puoli pysyy muuten samana, mutta summaan ilmestyy yksi uusi termi, nimittäin \(n+1\). Oikean puolen muutosta ei ole helppo nähdä suoraan, vaan tätä varten pitää laskea. Muutos on uusi arvo miinus vanha arvo eli \[\frac{(n+1)((n+1) + 1)}{2} - \frac{n(n+1)}{2}.\] Tämän saa helpoiten sievennettyä ottamalla \(n+1\):n yhteiseksi tekijäksi: \[\frac{(n+1)((n+1) + 1)}{2} - \frac{n(n+1)}{2} = (n+1)\left(\frac{n+2}{2} - \frac{n}{2}\right) = (n+1) \cdot 1 = n+1.\] Muutos on siis \(n+1\), niin kuin pitikin.
Mitä tästä hyötyy? Olemme edellä tarkastaneet, että yhtälö 1.1 pätee, kun \(n = 1, 2, 3, 4\). Lisäksi olemme tarkastaneet, että jos lukua \(n\) kasvattaa yhdellä, niin vasen ja oikea puoli muuttuvat saman verran, eli ne ovat edelleen yhtä suuria. Tästä seuraa, että yhtälö pätee myös suuremmilla \(n\):n arvoilla.
Todistus on täten valmis.
1.4 Esimerkki 3: Väritys

Ideana on miettiä ongelmaa induktiivisesti: Pienet tapaukset (kun suoria on esimerkiksi \(0, 1\) tai \(2\)) ovat helppoja. Mitä tapahtuu, kun kuvioon lisätään yksi suora? Jos voimme varmistaa, että aina uuden suoran lisäämisen jälkeen väritys edelleen onnistuu, niin haluttu väite pätee.
Yritetään tehdä tämä. Oletetaan siis, että olemme tähän asti saaneet värityksen aikaan esimerkiksi kolmen suoran tapauksessa.

Tutkitaan sitten tilannetta, jossa suoria on yksi enemmän.
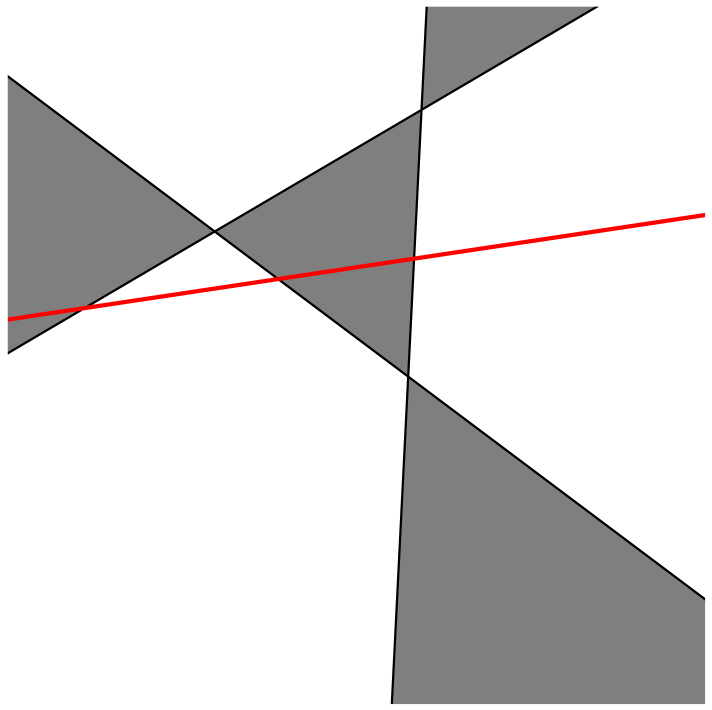
Mitä nyt? Väritys toimii muuten, mutta uuden suoran eri puolilla on alueita, jotka ovat vierekkäisiä ja samanvärisiä. Väritystä pitää tietysti muuttaa. Vaihdetaan väriä vaikkapa niissä alueissa, jotka ovat uuden suoran vieressä sen yläpuolella. Saadaan seuraava kuvio:
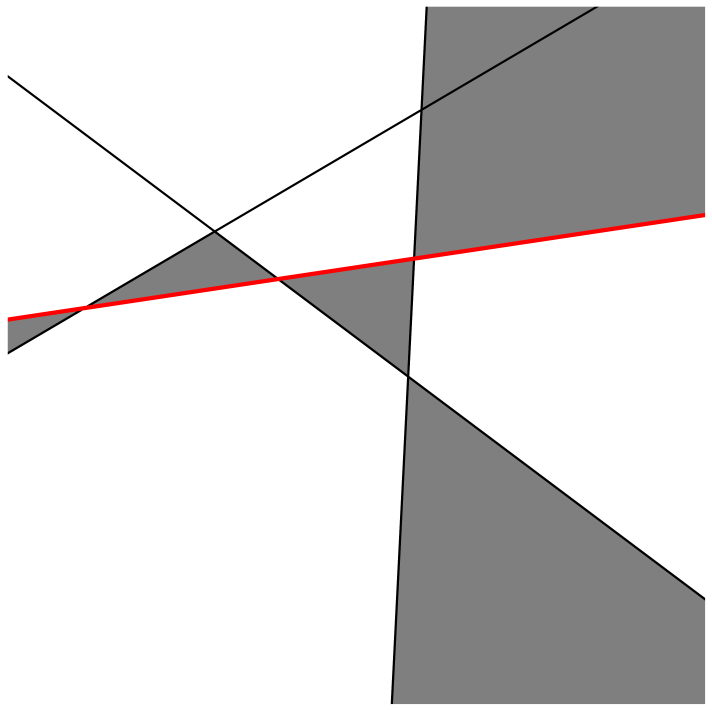
Väritystä pitää tietysti muuttaa vielä muidenkin uuden suoran yläpuolella olevien alueiden kohdalla:
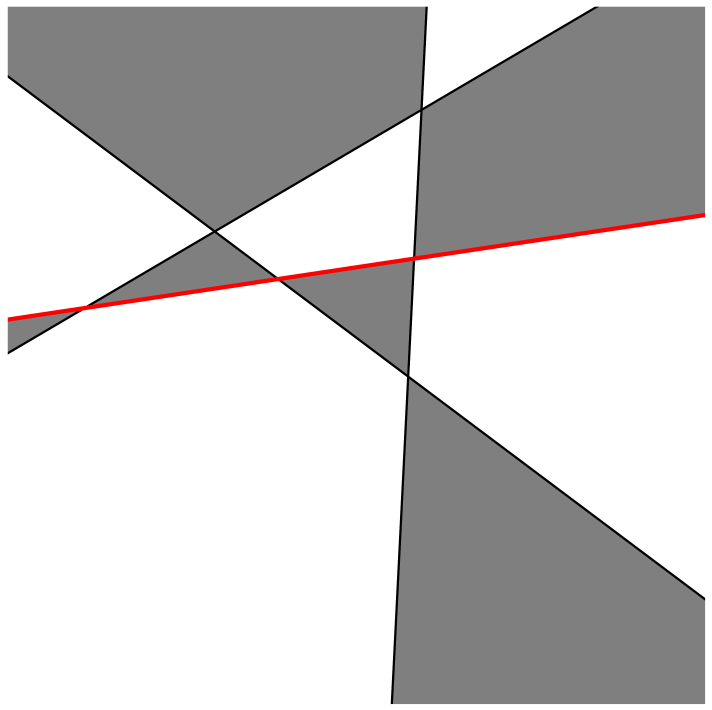
Tämä väritys toimii!
Eli yleisesti lisättäessä uusi suora vaihdetaan kaikkien toisella puolella suoraa olevien alueiden värit päinvastaisiksi. Tämä todella toimii: Tutkitaan joitakin kahta vierekkäistä aluetta. Jos ne ovat eri puolella uutta suoraa, ovat ne värien vaihtamisen takia erivärisiä. Jos ne ovat samalla puolella uutta suoraa, ovat ne erivärisiä, koska ne olivat ennen värien vaihtamista erivärisiä (lähdimme toimivasta värityksestä) ja värien vaihtaminen muuttaa joko molempien tai ei kummankaan alueen väriä.
1.5 Esimerkki 4: Merkkijonot
Vastaus on tietysti liian iso laskettavaksi suoraan. Yritetään laskea vastaus induktiivisesti tutkimalla lyhyempiä merkkijonoja. (Vertaa esimerkkiin 1.)
Yksikirjaimisia jonoja on tietysti \(3\). Kaksimerkkisiä kirjaimista \(a, b, c\) koostuvia jonoja on \(3 \cdot 3 = 9\) (koska ensimmäisen numeron voi valita kolmella tavalla, kuten myös toisen), ja näistä ainoastaan \(aa\) ei kelpaa. Siis kelpaavia kahden merkin jonoja on \(8\). Kolmimerkkisten kelpaavien jonojen määrä on jo hieman vaikeampi laskea, mutta niitä on \(22\): kaikista \(3 \cdot 3 \cdot 3 = 27\) merkkijonosta kelpaa kaikki paitsi \(aaa, aab, aac, baa, caa\).
Mietitään sitten induktion kannalta oleellista kysymystä: kuinka paljon mahdollisten merkkijonojen määrä kasvaa, kun pituutta kasvatetaan yhdellä? Vastaus ei ole aivan yksinkertainen: jos nykyinen merkkijono loppuu \(a\)-kirjaimeen, voi sitä jatkaa kahdella tavalla (lisäämällä loppuun \(b\):n tai \(c\):n), ja jos nykyinen merkkijono loppuu \(b\)- tai \(c\)-kirjaimeen, voi sitä jatkaa kolmella tavalla.
Tästä syystä on luontevaa tutkia erikseen, kuinka moni merkkijono päättyy \(a\)-kirjaimeen ja kuinka moni \(b\)- tai \(c\)-kirjaimeen. Näitäkin määriä voi laskea induktiivisesti, ja määrät riippuvat yhtä merkkiä lyhyempien merkkijonojen määristä.
Laskemista varten määritellään \(f(n)\) olemaan niiden \(n\)-kirjaimisten jonojen määrä, joissa ei ole kahta peräkkäistä \(a\)-kirjainta ja jotka päättyvät \(a\)-kirjaimeen, ja \(g(n)\) olemaan niiden \(n\)-kirjaimisten jonojen määrä, joissa ei ole kahta peräkkäistä \(a\)-kirjainta ja jotka eivät pääty \(a\)-kirjaimeen. Tehtävän vastaus on tällöin \(f(5) + g(5)\).
Määrät \(f(n)\) ja \(g(n)\) riippuvat toisistaan seuraavilla tavoilla: \[f(n) = g(n-1) \qquad(1.2)\] ja \[g(n) = 2f(n-1) + 2g(n-1). \qquad(1.3)\]
Perustelut: Jokainen \(a\)-kirjaimeen päättyvä \(n\)-kirjaiminen jono saadaan ottamalla jokin \(n-1\)-merkkinen jono, joka ei pääty \(a\):han, ja lisäämällä loppuun \(a\)-kirjain. Yhtälö 1.2 seuraa tästä.
Jokainen \(n\)-kirjaiminen jono, joka ei pääty \(a\)-kirjaimeen saadaan ottamalla mikä vain \(n-1\)-kirjaiminen jono ja lisäämällä sen loppuun \(b\)- tai \(c\)-kirjain. Tästä saadaan yhtälö 1.3.
Alkuarvot saadaan helposti: \(f(1) = 1\) ja \(g(1) = 2\). Käyttämällä rekursioyhtälöitä 1.2 ja 1.3 voimme nyt laskea luvut \(f(2)\) ja \(g(2)\), sitten luvut \(f(3)\) ja \(g(3)\) ja niin edelleen. Alla on taulukko näistä arvoista.
| \(f(1)=1\) | \(g(1)=2\) |
| \(f(2)=2\) | \(g(2)=6\) |
| \(f(3)=6\) | \(g(3)=16\) |
| \(f(4)=16\) | \(g(4)=44\) |
| \(f(5)=44\) | \(g(5)=120\) |
Vastaus on siis \(44 + 120 = 164\).
1.6 Tehtäviä
Tehtävä 1. Lammen veden päällä on rivissä \(11\) lumpeenlehteä. Sammakko on rivin ensimmäisellä lehdellä ja haluaa päästä rivin viimeiselle lumpeenlehdelle. Sammakko pystyy hyppäämään kerrallaan korkeintaan kaksi lehteä eteenpäin. Kuinka monella eri tavalla sammakko voi pomppia ensimmäiseltä lehdeltä viimeiselle?
Tehtävä 2. Annalla on rajaton määrä neljän ja seitsemän euron kolikoita. Mikä on suurin (kokonaisluku)rahamäärä, jota hän ei voi muodostaa kolikoilla?
Tehtävä 3. Laske/sievennä: \(1 + 2 + 4 + 8 + \ldots + 2^{99}\).
Tehtävä 4. Kuinka monella tavalla \(2 \times 10\) -laudan voi peittää \(2 \times 1\) -dominoilla? (Dominoita saa kääntää, mutta ne eivät saa mennä toistensa päälle tai laudan ulkopuolelle.)
Tehtävä 5. Kuinka monta lävistäjää \(100\)-kulmiolla on? (Esimerkiksi nelikulmiolla on \(2\) lävistäjää ja viisikulmiolla \(5\).)
Tehtävä 6. Osoita, että kaikilla kokonaisluvuilla \(n \ge 6\) pätee \(2^n \ge 10n\).
Tehtävä 7. Tasossa on \(100\) suoraa, joista mitkään kaksi eivät ole yhdensuuntaisia eivätkä mitkään kolme leikkaa samassa pisteessä. Kuinka moneen alueeseen ne jakavat tason?
Tehtävä 8. Kuinka monta sellaista kymmenkirjaimista merkkijonoa, jossa jokainen merkki on \(a\) tai \(b\) ja jossa on pariton määrä \(a\) kirjaimia, on olemassa?