7  Kongruenssit

Tekijä

Olli Järviniemi

7.1 Johdanto

Kongruenssit ovat kätevä tapa puhua jaollisuuksista ja jakojäännöksistä. Alla esitetään kongruenssien idea, käydään läpi esimerkkitehtäviä ja päätetään harjoitustehtävillä.

7.2 Kongruenssien idea

Lähdetään liikkeelle seuraavasta tehtävästä. Tehtävä

Tehtävä 7.1 Liitutaululla on kaksi positiivista kokonaislukua. Ensimmäisen viimeinen numero on \(2\) ja toisen \(3\). Mikä on niiden summan viimeinen numero?

Vaikkei luvuista tiedetä mitään muuta kuin niiden viimeiset numerot, niin voidaan sanoa, että vastaus on \(2 + 3 = 5\). Summassa ykkösten paikalla oleviin numeroihin vaikuttaa nimittäin vain summattavien ykkösten paikalla olevat numerot, kuten näkee esimerkiksi allekkain yhteenlaskusta:

Kuva 1. Summan viimeinen numero on viimeisten numeroiden summa.

Oli kysymysmerkkien paikalla mitä numeroita tahansa, summan viimeinen numero on \(5\).

Huomataan, että myös tulolla on sama ominaisuus: jos kahdesta luvusta toisen viimeinen numero on \(2\) ja toisen \(3\), on tulon viimeinen numero \(2 \cdot 3 = 6\). Tämän näkee tutkimalla allekkain kertolaskua:

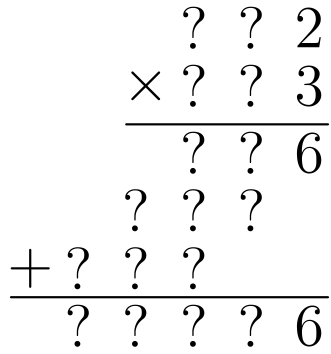
Kuva 1. Tulon viimeinen numero on kerrottavien viimeisten numeroiden tulo.

Oli kysymysmerkkien paikalla mitä numeroita tahansa, tulon viimeinen numero on \(6\).

Tietysti nämä samat ominaisuudet pätevät edelleen, vaikka viimeiset numerot olisivat kahden ja kolmen sijasta vaikkapa \(6\) ja \(7\). Tällöin summan viimeinen numero on \(3\), koska \(6+7 = 13\), ja tulon viimeinen numero on \(2\), koska \(6 \cdot 7 = 42\).

Vaikka tämä voi aluksi tuntua hassulta, luvun viimeisen numeron voi ajatella olevan jakojäännös, kun luku jaetaan kymmenellä. Olemme siis yllä perustelleet, että summan/tulon jakojäännös (kymmenellä jaettaessa) on sama kuin jakojäännöksien summan/tulon jakojäännös kymmenellä jaettaessa.

Kymmenen ei ole tässä suhteessa mitenkään erityinen luku. Olemme vain tottuneet esittämään lukuja kymmenjärjestelmässä, jossa on \(10\) numeroa (\(0, 1, 2, 3, 4, 5, 6, 7, 8, 9\)). Samat ominaisuudet pätevät edelleen, vaikka tutkisimme jakojäännöksiä vaikkapa seitsemällä jaettaessa. Esimerkiksi jos luvun \(a\) jakojäännös seitsemällä jaettaessa on kaksi ja luvun \(b\) neljä, saadaan lukujen \(a+b\) ja \(ab\) jakojäännökset summaamalla tai kertomalla jakojäännökset \(2\) ja \(4\) (ja ottamalla siitä vielä tarvittaessa jakojäännös).

Jakojäännöksistä puhumista helpottavat seuraavaksi esiteltävät kongruenssit.

7.3 Kongruenssit

Esitetään ensiksi määritelmä ja avataan sitä sitten esimerkein.

Määritelmä 7.1 Olkoot \(a, b\) ja \(m\) kokonaislukuja (\(m \ge 1\)). Jos luvuilla \(a\) ja \(b\) on sama jakojäännös luvulla \(m\) jaettaessa (eli toisin sanoen \(m\) jakaa luvun \(a-b\)), niin merkitään \[a \equiv b \pmod{m}.\] Sanotaan, että \(a\) ja \(b\) ovat kongruentteja modulo \(m\). Lukua \(m\) kutsutaan moduloksi. Puhekielessä sanotaan usein lyhyesti ”\(a\) on \(b\) modulo \(m\)”.

Esimerkkejä:

  • \(a \equiv 0 \pmod{2}\) tarkoittaa, että \(a\):n jakojäännös kahdella jaettaessa on \(0\) eli että \(a\) on parillinen
  • \(a \equiv 1 \pmod{2}\) tarkoittaa, että \(a\):n jakojäännös kahdella jaettaessa on \(1\) eli että \(a\) on pariton
  • \(a \equiv b \pmod{2}\) tarkoittaa, että \(a\):lla ja \(b\):llä on samat jakojäännökset kahdella jaettaessa eli että \(a\) ja \(b\) ovat joko molemmat parillisia tai molemmat parittomia
  • \(a \equiv 3 \pmod{10}\) tarkoittaa, että \(a\):n jakojäännös kymmenellä jaettaessa on \(3\) eli että luvun \(a\) viimeinen numero on \(3\)

Lisää esimerkkejä konkreettisilla luvuilla:

  • \(5 \equiv 1 \pmod{2}\)
  • \(8 \equiv 2 \pmod{3}\)
  • \(53 \equiv 23 \pmod{10}\)
  • \(4 \equiv -1 \pmod{5}\)

Suomen kielessä on erikseen sana ”pariton” luvuille, joiden jakojäännös kahdella jaettaessa on yksi ja ”parillinen” luvuille, joiden jakojäännös kahdella jaettaessa on nolla. Ehkäpä tästä syystä on helppoa hahmottaa parillisia ja parittomia lukuja ja olla samaa mieltä esimerkiksi väitteestä ”parillisen ja parittoman luvun summa on pariton”. Ikävä kyllä vastaavia sanoja ei ole esimerkiksi modulolle \(3\): suomen kielessä ei ole sanaa sille, että luvun jakojäännös kolmella jaettaessa on kaksi. Tämä tekee kongruenssien sisäistämisestä vaikeampaa, vaikka kyse on loppukädessä tutusta ideasta.

7.4 Kongruenssien perusominaisuudet

Kongruenssien idea -osion esimerkit voidaan kirjoittaa kongruenssien avulla seuraavasti:

  • Jos \(a \equiv 2 \pmod{10}\) ja \(a \equiv 3 \pmod{10}\), niin \(a + b \equiv 5 \pmod{10}\)
  • Jos \(a \equiv 2 \pmod{10}\) ja \(a \equiv 3 \pmod{10}\), niin \(a \cdot b \equiv 6 \pmod{10}\)
  • Jos \(a \equiv 6 \pmod{10}\) ja \(a \equiv 7 \pmod{10}\), niin \(a + b \equiv 3 \pmod{10}\)
  • Jos \(a \equiv 6 \pmod{10}\) ja \(a \equiv 7 \pmod{10}\), niin \(a \cdot b \equiv 2 \pmod{10}\)

Idea on siis, että kongruenssiyhtälöitä voi summata ja kertoa keskenään. Alla oleva lause kertoo tästä.

Lause 7.1 (Kongruenssien peruslaskutoimitukset) Olkoot \(a, b, c, d\) ja \(m\) kokonaislukuja (\(m \ge 1\)). Oletetaan, että pätee \[a \equiv b \pmod{m} \qquad \text{ja} \qquad c \equiv d \pmod{m}.\] Tällöin pätee \[a + c \equiv b + d \pmod{m}, \qquad a - c \equiv b - d \pmod{m} \qquad \text{ja} \qquad ac \equiv bd \pmod{m}.\]

Käytännössä lauseesta seuraa, että kongruenssiyhtälöitä voi käsitellä pitkälti kuten tavallisia yhtälöitä. Tätä ajatusta demonstroidaan alla parin esimerkin kautta ja myöhemmin tehtävissä.

Tarkkoihin todistuksiin palataan myöhemmissä teksteissä sen jälkeen, kun on saatu enemmän tuntumaa kongruensseista. Tulosten pitäisi kuitenkin käydä järkeen, olemmehan pitkälti perustelleet laskusäännöt tapauksessa \(m = 10\).

7.5 Esimerkkisovelluksia

7.5.1 Esimerkki 1: Viimeinen numero

Tehtävä 7.2 Mikä on luvun \(17^{100}\) viimeinen numero?

Luku on tietysti aivan liian suuri laskettavaksi ilman laskinta. Käytetään siis kongruensseja apuna.

Viimeinen numero vastaa jakojäännöstä kymmenellä jaettaessa, joten haluamme laskea, mitä \(17^{100}\) on modulo kymmenen. Ensinnäkin tulos riippuu vain kantaluvun ykkösten paikalla olevasta numerosta: \[17^{100} \equiv 7^{100} \pmod{10}.\] (Tarkka perustelu: Tiedämme, että \(17 \equiv 7 \pmod{10}\). Kongruenssiyhtälöitä saa kertoa keskenään. Kerrotaan tämä yhtälö itsensä kanssa. Saamme \(17^2 \equiv 7^2 \pmod{10}\). Kerrotaan uudestaan yhtälön \(17 \equiv 7 \pmod{10}\) kanssa. Saamme \(17^3 \equiv 7^3 \pmod{10}\). Jatketaan näin.)

Huomataan siis, että kongruenssiyhtälön saa korottaa puolittain johonkin potenssiin.

Luvun \(7^{100}\) viimeisen numeron laskeminen ei tosin ole sekään helppoa. Avainidea on laskea muutama ensimmäinen arvo ja huomata säännönmukaisuus: \[7^1 \equiv 7 \pmod{10},\] \[ \begin{aligned} & 7^2 \equiv 7 \cdot 7 \equiv 49 \equiv {\color{red} 9} \pmod{10}, \\ & 7^3 \equiv 7 \cdot 7^2 \equiv 7 \cdot {\color{red} 9} \equiv 63 \equiv {\color{green} 3} \pmod{10}, \\ & 7^4 \equiv 7 \cdot 7^3 \equiv 7 \cdot {\color{green} 3} \equiv 21 \equiv {\color{blue} 1} \pmod{10}, \\ & 7^5 \equiv 7 \cdot 7^4 \equiv 7 \cdot {\color{blue} 1} \equiv {\color{orange} 7} \qquad \ \pmod{10}, \\ & 7^6 \equiv 7 \cdot 7^5 \equiv 7 \cdot {\color{orange} 7} \equiv 49 \equiv 9 \pmod{10}. \end{aligned} \] (Käytämme tässä ahkerasti kongruenssien laskusääntöjä.) Säännönmukaisuus on selvä: viimeinen numero on vuorotellen \(7, 9, 3, 1\), ja sitten jono alkaa taas alusta. Aina neljällä jaollisilla eksponenteilla viimeinen numero on \(1\), ja koska \(100\) on jaollinen neljällä, on luvun \(7^{100}\) viimeinen numero \(1\).

Täten myös luvun \(17^{100}\) viimeinen numero on \(1\).

7.5.2 Esimerkki 2: Kolmen jaollisuussääntö

Tehtävä 7.3 Osoita, että luku on jaollinen kolmella täsmälleen silloin, kun sen numeroiden summa on jaollinen kolmella.

Esimerkiksi jos valitaan luku \(816\), on sen numeroiden summa \(8 + 1 + 6 = 15\), joka on jaollinen kolmella. Siis alkuperäinen luku on myös jaollinen kolmella. (Tosiaan: \(816 = 3 \cdot 272\).)

Tehtävän ratkaisua varten todetaan ensin, että \[10 \equiv 1 \pmod{3}.\] Edellisessä esimerkissä todettiin, että kongruenssiyhtälön saa korottaa puolittain potenssiin. Todetaan siis, että mikä tahansa kymmenen potenssi on \(1 \pmod{3}\): \[10^k \equiv 1 \pmod{3}\] kaikilla \(k = 1, 2, 3, \ldots\).

Todistetaan sitten itse väite. Otetaan jokin positiivinen kokonaisluku, ja olkoot sen numerot merkitsevimmästä epämerkitsevimpään \(a_n, a_{n-1}, \ldots , a_2, a_1, a_0\). Luku on siis \[a_n \cdot 10^n + a_{n-1} \cdot 10^{n-1} + \ldots + a_2 \cdot 10^2 + a_1 \cdot 10 + a_0.\] Kongruenssien laskusäännöillä ja edellisen aputuloksen nojalla kymmenen potenssit voidaan korvata ykkösellä, joten \[ \begin{aligned} & \ a_n \cdot 10^n + a_{n-1} \cdot 10^{n-1} + \ldots + a_2 \cdot 10^2 + a_1 \cdot 10 + a_0 \\ \equiv & \ a_n \cdot 1 \ \ \ + a_{n-1} \cdot 1 \ \ \ \ \ \ + \ldots + a_2 \cdot 1 \ \ + a_1 \cdot 1 \ \ + a_0 \pmod{3}. \end{aligned} \] Täten luvulla ja sen numeroiden summalla on sama jakojäännös kolmella jaettaessa. Erityisesti toinen on jaollinen kolmella täsmälleen silloin kuin toinen on. Tämä on haluttu väite.

Kommentti. Todistus toimii samalla tavalla jos luvun \(3\) korvaa luvulla \(9\). Oleellista on vain, että \(10 \equiv 1 \pmod{9}\). Tämä yhtälö voidaan taas korottaa johonkin potenssiin, mistä viimeistely tehdään samalla tavalla kuin kolmosen kohdalla.

7.6 Tehtäviä

Tehtävä 1. Määritellään lukujono \(a_1, a_2, \ldots\) niin, että sen ensimmäinen luku on \(1\) ja seuraava luku on aina kaksi kertaa edellinen plus yksi: \(a_1 = 1\) ja \(a_{n+1} = 2a_n + 1\) kaikilla \(n \ge 1\). (Ensimmäiset luvut ovat siis \(1, 3, 7, 15, \ldots\)) Mikä on jakojäännös, kun \(a_{100}\) jaetaan viidellä?

Tehtävä 2.

  1. Liitutaululla on kolme kokonaislukua. Osoita, että niistä voidaan valita kaksi, joiden erotus on jaollinen kahdella.
  2. Liitutaululla on neljä kokonaislukua. Osoita, että niistä voidaan valita kaksi, joiden erotus on jaollinen kolmella.
  3. Liitutaululla on kolme kokonaislukua. Osoita, että niistä voidaan valita yksi tai useampi, joiden summa on jaollinen kolmella.

Tehtävä 3. Onko olemassa kokonaislukua \(x\), jolla \(12x + 6\) on jaollinen

  1. neljällä?
  2. viidellä?

Tehtävä 4. Onko olemassa kokonaislukua \(x\), jolla \(x^2 + 1\) on jaollinen kolmella? Entä viidellä tai seitsemällä?

Tehtävä 5. Montako alkulukua \(p\), joilla myös \(p+2\) ja \(p+4\) ovat alkulukuja, on olemassa?

Tehtävä 6. Tutkitaan seuraavaa muunnelmaa numeroiden summasta: sen sijaan että lasketaan yhteen luvun kaikki numerot, niin vähennetäänkin aina joka toinen numero. Esimerkiksi aloittamalla luvusta \(123456\) saadaan \(1 - 2 + 3 - 4 + 5 - 6 = -3\). Osoita seuraava sääntö yhdellätoista jaollisuudelle: luku on jaollinen yhdellätoista täsmälleen silloin, kun sen muunneltu numeroiden summa on jaollinen yhdellätoista.

Tehtävä 7. Liitutaululla on aluksi kokonaisluku \(1\). Jos liitutaulun nykyinen luku on \(x\), sen voi korvata yhdellä seuraavista luvuista: \(x-5, x+10\) tai \(3x+1\). Onko näitä operaatioita toistamalla mahdollista päästä lukuun \(2\)?