24 Pisteen potenssi ja radikaaliakselit

Tekijä

Olli Järviniemi

24.1 Johdanto

Tässä tekstissä esitetään uusi menetelmä geometrian tehtävien ratkaisemiseen: pisteen potenssi ja radikaaliakselit. Työkalu pohjautuu ennestään tuttuihin yhdenmuotoisiin kolmioihin ja jännenelikulmioihin, mutta menetelmä antaa uudenlaista perspektiiviä geometrian konfiguraatioihin.

24.2 Pisteen potenssi

24.2.1 Ympyrän ulkopuolinen tapaus

Piirretään ympyrä ja valitaan piste \(P\) sen ulkopuolelta. Piirretään \(P\):n kautta suora, joka leikkaa ympyrän pisteissä \(A\) ja \(B\). Pisteen potenssi sanoo, että pituuksien tulo \(PA \cdot PB\) ei riipu valitusta suorasta.

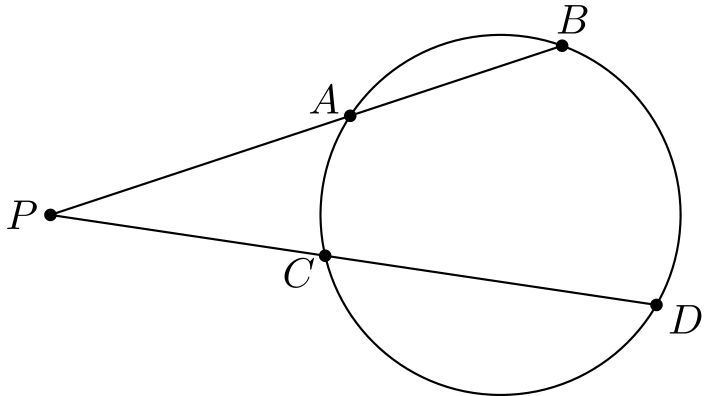
Kuva 24.1: Valitusta suorasta riippumatta tulo on sama: \(PA \cdot PB = PC \cdot PD\).

Todistus. Idea on, että kuvion jännenelikulmio antaa yhtä suuria kulmia, mistä saadaan pituusinformaatiota yhdenmuotoisten kolmioiden kautta.

Osoitetaan, että kolmiot \(PAC\) ja \(PDB\) ovat yhdenmuotoisia. Niillä on yksi yhteinen kulma kärjessä \(P\). Lisäksi koska \(ABDC\) on jännenelikulmio, pätee \[\angle PAC = 180^{\circ} - \angle CAB = \angle BDP,\] eli toisetkin kulmat ovat samat ja kolmiot ovat yhdenmuotoisia. Täten sivujen suhteet ovat samat: \[\frac{PA}{PC} = \frac{PD}{PB}.\] Väite seuraa.

24.2.2 Ympyrän sisäpuolinen tapaus

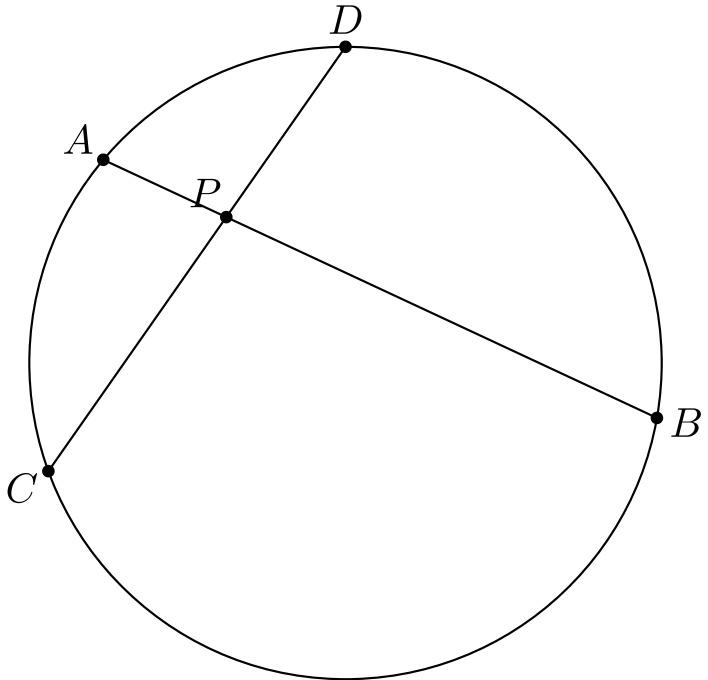
Pisteen potenssi toimii myös, vaikka \(P\) olisi kolmion sisäpuolella. Todistus on sama kuin edellä: kolmiot \(PAC\) ja \(PDB\) ovat taas yhdenmuotoisia, koska \(ACBD\) on jännenelikulmio.

Kuva 24.2: Yhdenmuotoisilla kolmioilla saadaan taas \(PA \cdot PB = PC \cdot PD\).

24.2.3 Tangenttitapaus

Huomioidaan vielä, että pisteen potenssi toimii siinäkin tapauksessa, jossa suora on tangentti ympyrälle. Tämän voi ajatella olevan tapaus, jossa \(A = B\).

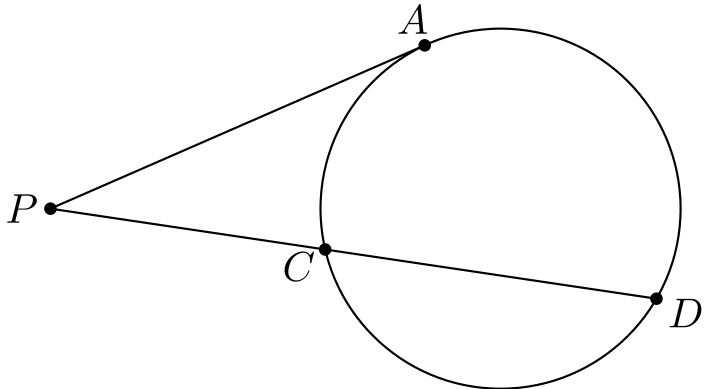
Odotetusti taas pätee \(PA^2 = PC \cdot PB\).

Ainoa muutos todistukseen on, että käytetään kehäkulmalauseen tangenttiversiota, jonka nojalla \(\angle PAC = \angle ADP\). Vastaavasti kuin aiemmin kolmiot \(PAC\) ja \(PDA\) ovat yhdenmuotoisia, mistä väite seuraa.

24.2.4 Pisteen potenssi

Yllä käsitellylle tulolle voi antaa kohtuullisen yksinkertaisen kaavan: jos kuvassa 24.1 valitaan suora niin, että \(AB\) on ympyrän halkaisija, niin pätee \[PA \cdot PB = (PO - r)(PO + r) = PO^2 - r^2,\] missä \(O\) on ympyrän keskipiste ja \(r\) on ympyrän säde. Sanotaan, että pisteen \(P\) potenssi \(O\)-keskisen \(r\)-säteisen ympyrän suhteen on \(PO^2 - r^2\).

Huomaa, että jos \(P\) on ympyrän sisällä (kuten kuvassa 24.2), niin \(PO^2 - r^2\) on negatiivinen. Jos \(AB\) on kuvan 24.2 tapauksessa ympyrän halkaisija, niin \(PA \cdot PB = (r - PO)(PO + r) = r^2 - PO^2\), eli vähennettävät ovat eri järjestyksessä. Tästä huolimatta pisteen potenssi määritellään aina olemaan \[PO^2 - r^2,\] oli piste ympyrän sisällä tai ei. On nimittäin kätevämpää, kun käytetään samaa kaavaa kaikille tapauksille, kuten nähdään seuraavaksi radikaaliakseleita käsitellessä.

Huomaa myös, että pisteen potenssi on \(0\) silloin, kun \(P\) on ympyrän kehällä.

24.3 Radikaaliakselit

Valitaan jotkin kaksi ympyrää. Missä ovat ne pisteet, joiden pisteen potenssit kummankin ympyrän suhteen ovat samat?

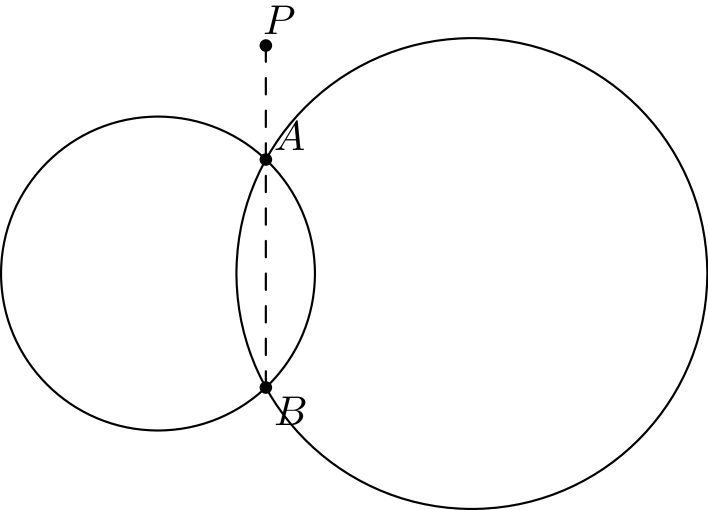
Kuva 24.3: Tapaus, jossa kaksi ympyrää leikkaavat.

Tutkitaan esimerkin vuoksi kuvan 24.3 tapausta. Huomataan, että ainakin leikkauspisteet \(A\) ja \(B\) toteuttavat ehdon: niiden pisteen potenssi molempien ympyröiden suhteen on \(0\). Oikeastaan mikä tahansa suoran \(AB\) piste \(P\) toteuttaa ehdon, koska \(P\):n potenssi molempien ympyröiden suhteen on \(PA \cdot PB\).

Osoittautuu, että muita ehdon toteuttavia pisteitä ei ole, eli saman pisteen potenssin omaavien pisteiden joukko on suora. Tätä suoraa kutsutaan ympyröiden radikaaliakseliksi. Radikaaliakseli on suora silloinkin, kun ympyrät eivät leikkaa.

Lause 24.1 (Radikaaliakselien peruslause) Olkoot \(\omega_1\) ja \(\omega_2\) kaksi ympyrää, joiden keskipisteet eivät ole samat. Tällöin ne pisteet, joiden potenssit ympyröiden \(\omega_1\) ja \(\omega_2\) suhteen ovat samat, muodostavat suoran (jota kutsutaan ympyröiden radikaaliakseliksi). Lisäksi

radikaaliakseli on kohtisuorassa ympyröiden \(\omega_1\) ja \(\omega_2\) keskipisteiden välistä janaa kohden
jos \(\omega_1\) ja \(\omega_2\) leikkaavat, radikaaliakseli kulkee leikkauspisteen/leikkauspisteiden kautta.

Todistus. Idea lyhyesti: laitetaan tilanne koordinaatistoon ja lasketaan.

Laitetaan ympyrät koordinaatistoon. Voimme asettaa koordinaatiston niin, että ympyröiden keskipisteet ovat \(x\)-akselilla. Olkoon siis ympyrän \(\omega_1\) keskipiste \((x_1, 0)\) ja säde \(r_1\), ja olkoon vastaavasti ympyrän \(\omega_2\) keskipiste \((x_2, 0)\) ja säde \(r_2\).

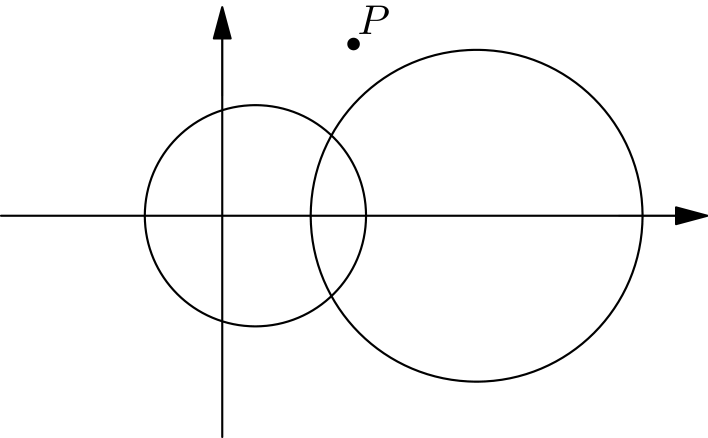
Valitaan sitten jokin piste \(P = (x, y)\) ja tutkitaan, onko sen pisteen potenssit ympyröiden suhteen samat.

Pisteen \(P\) potenssi ensimmäisen ympyrän suhteen on \[(x - x_1)^2 + y^2 - r_1^2\] ja toisen suhteen \[(x - x_2)^2 + y^2 - r_2^2.\] Saadaan yhtälö \[(x - x_1)^2 + y^2 - r_1^2 = (x - x_2)^2 + y^2 - r_2^2.\] Termit \(y^2\) katoavat. Siirretään \(-r_1^2\) oikealle ja \((x - x_2)^2\) vasemmalle: \[(x - x_1)^2 - (x - x_2)^2 = r_1^2 - r_2^2.\] Kertomalla vasen puoli auki tämä sievenee muotoon \[2x(x_2 - x_1) + x_1^2 - x_2^2 = r_1^2 - r_2^2.\] Tämä on ensimmäisen asteen yhtälö muuttujan \(x\) suhteen (huomaa, että ympyröiden keskipisteet eivät ole samat, joten \(x_1 \neq x_2\)), joten sillä on täsmälleen yksi ratkaisu.

Yllä oleva päättely osoittaa, että \(P\) toteuttaa halutun ehdon täsmälleen silloin, kun sen \(x\)-koordinaatti on sopiva. Tämä tarkoittaa, että halutut pisteet ovat jonkin \(y\)-akselin suuntaisen suoran pisteet. Tämä todistaa lauseen pääväitteen ja kohdan (i). Kohta (ii) on selvä, koska leikkauspisteiden potenssit ympyröiden suhteen ovat nollia.

24.4 Kolmen ympyrän radikaaliakselit

Seuraava tulos on välillä hyödyllinen sen osoittamiseksi, että kolme suoraa leikkaavat samassa pisteessä.

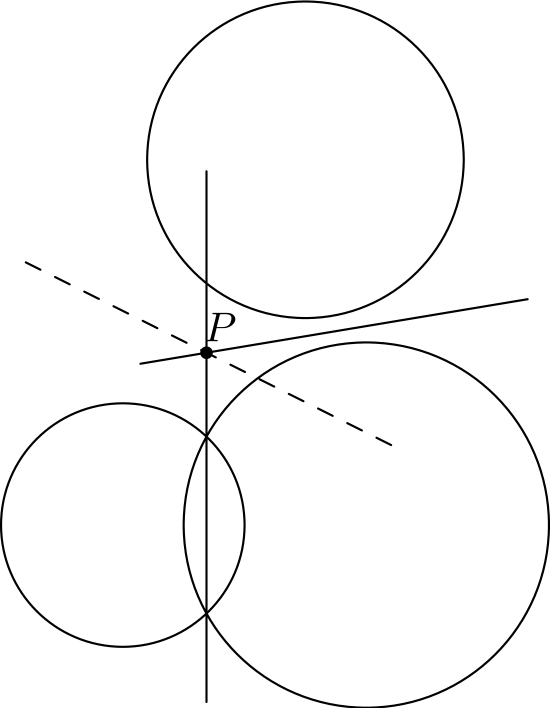
Lause 24.2 (Kolmen ympyrän radikaaliakselit) Olkoot \(\omega_1, \omega_2\) ja \(\omega_3\) ympyröitä, joiden keskipisteet eivät sijaitse samalla suoralla. Olkoon \(\ell_{12}\) ympyröiden \(\omega_1\) ja \(\omega_2\) radikaaliakseli. Määritellään \(\ell_{13}\) ja \(\ell_{23}\) vastaavasti. Tällöin \(\ell_{12}, \ell_{13}\) ja \(\ell_{23}\) leikkaavat samassa pisteessä.

Kolme ympyrää ja niiden radikaaliakselit.

Todistus. Olkoon \(P\) suorien \(\ell_{12}\) ja \(\ell_{23}\) leikkauspiste.¹ Nyt pisteen \(P\) potenssit ympyröiden \(\omega_1\) ja \(\omega_2\) suhteen ovat sama, kuten myös ympyröiden \(\omega_2\) ja \(\omega_3\) suhteen. Täten \(P\):n potenssit ympyröiden \(\omega_1\) ja \(\omega_3\) suhteen ovat samat, eli \(P\) on suoralla \(\ell_{23}\).

¹ Tätä vaihetta varten tarvitaan tieto, etteivät radikaaliakselit ole yhdensuuntaisia. Tämä vastaa sitä, etteivät ympyröiden keskipisteet ole samalla suoralla.

24.5 Esimerkkitehtäviä

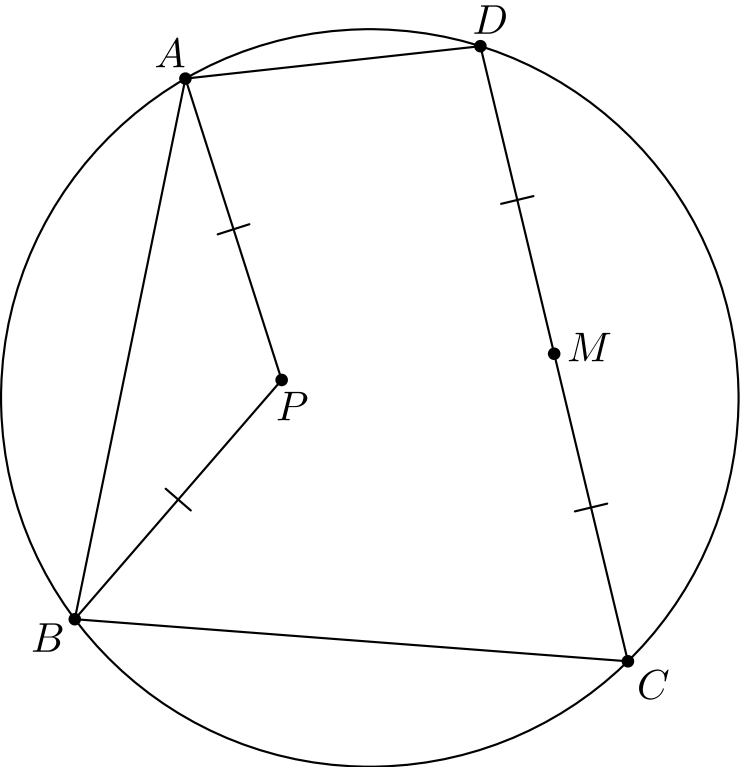
Tehtävä 24.1 Olkoon \(ABCD\) jännenelikulmio, jonka sivut \(AB\) ja \(CD\) eivät ole yhdensuuntaisia. Olkoon \(M\) sivun \(CD\) keskipiste. Olkoon \(P\) sellainen piste jännenelikulmion \(ABCD\) sisällä, että \(PA = PB = CM\). Todista, että \(AB, CD\) ja janan \(MP\) keskinormaali kulkevat saman pisteen kautta.

Ratkaisu. Piirretään \(P\)- ja \(M\)-keskiset ympyrät, joiden säde on \(PA\), ja käytetään lausetta 24.2 näille kahdelle ympyrälle ja jännenelikulmion \(ABCD\) ympärysympyrälle. Nyt \(P\)- ja \(M\)-keskisten ympyröiden radikaaliakseli on janan \(PM\) keskinormaali, \(P\)-keskisen ympyrän ja \(ABCD\):n ympärysympyrän radikaaliakseli on \(AB\) ja \(M\)-keskisen ympyrän ja \(ABCD\):n ympärysympyrän radikaaliakseli on \(CD\).

Avainidea on lisätä kuvioon kaksi ympyrää.

Kommentti. Tämä on hieman tylsä ”yhden idean tehtävä”, mutta se on silti ihan hyvä esimerkki demonstroimaan menetelmiä. Tehtävissä harvemmin on suoraan piirrettynä kaikkia relevantteja ympyröitä tai ylipäätään relevantteja asioita, vaan niitä pitää hoksata lisätä itse kuvioihin. Tässä tehtävässä yhtä pitkät janat olivat melko selkeä vinkki ympyröiden konstruoimiseen.

Tehtävä 24.2 Olkoon \(ABC\) teräväkulmainen kolmio. Olkoot \(M\) ja \(N\) sen ympyrän, jonka halkaisija on \(AB\), ja kolmion \(ABC\) kärjestä \(C\) piirretyn korkeusjanan (tai sen jatkeen) leikkauspisteet. Olkoot vastaavasti \(P\) ja \(Q\) sen ympyrän, jonka halkaisija on \(AC\), ja kolmion \(ABC\) kärjestä \(B\) piirretyn korkeusjanan (tai sen jatkeen) leikkauspisteet. Osoita, että \(NPMQ\) on jännenelikulmio.

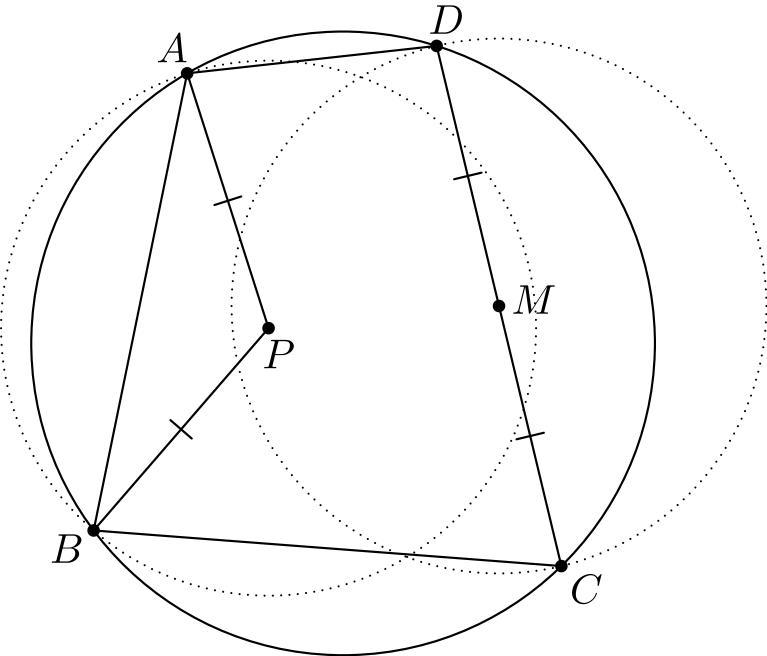
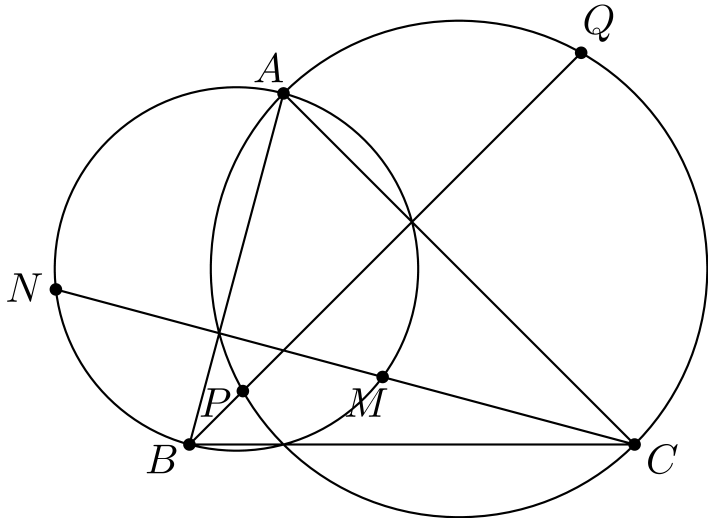
Kuviosta huomataan heti muutama ominaisuus: ympyrät näyttävät leikkaavan janalla \(BC\) ja korkeusjana (korkeussuora) \(CN\) leikkaa \(AC\)-halkaisijaista ympyrää janalla \(AB\). Nämä ovat kuitenkin tuttuja juttuja: kaikki perustuu siihen, että kolmion kärjet ja korkeusjanojen kantapisteet antavat paljon jännenelikulmiota.

Tehtävää voisi yrittää ratkaista puhtaasti kulmia jahtaamalla. Konfiguraatiosta nimittäin tiedetään aika paljon kulmia, joten tämä on houkutteleva vaihtoehto. Tulosta ei kuitenkaan synny.

Kuvitellaan hetkeksi, että \(NPMQ\) on jännenelikulmio. Tällöin kuviossa on kolme ympyrää ja siten myös kolme radikaaliakselia, jotka leikkaavat samassa pisteessä. Mikä tämä piste on?

Niiden ympyröiden, joiden halkaisijat ovat \(AB\) ja \(AC\), radikaaliakseli on pisteestä \(A\) piirretty korkeusjana. Jos \(NPMQ\) on jännenelikulmio, sen ympärysympyrän ja \(AB\)-halkaisijaisen ympyrän radiaaliakseli on suora \(MN\) eli kärjestä \(C\) piirretty korkeusjana. Viimeinen radikaaliakseli on \(B\):stä piirretty korkeusjana. Leikkauspiste on siis kolmion \(ABC\) ortokeskus.

Tämä ei ratkaise tehtävää, mutta antaa vihjeen siitä, mistä päin ratkaisua kannattaa etsiä. Lisätään kärjestä \(A\) piirretty korkeusjana ja ortokeskus kuvioon:

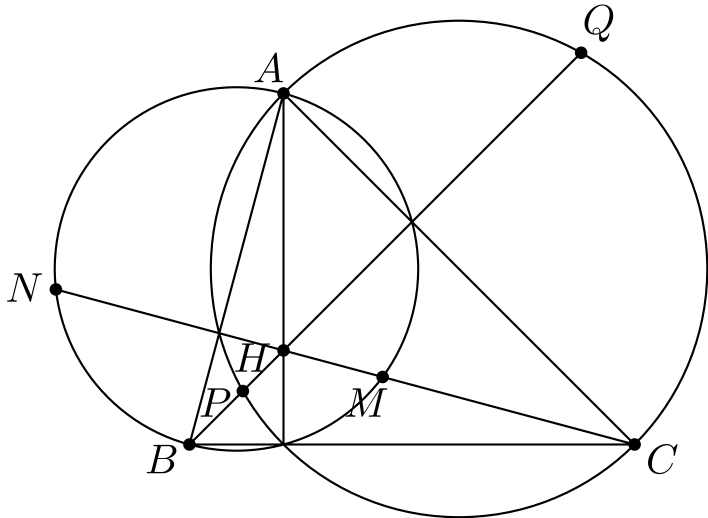
Ortokeskus ja \(A\)-korkeusjana piirrettynä kuvioon.

Nyt idea on seuraava: Jos \(NPMQ\) on jännenelikulmio, pisteen potenssilla \(HM \cdot HN = HP \cdot HQ\). Osaamme kuitenkin todistaa tämän suoraan. Jos nimittäin \(D\) on kärjestä \(A\) piirretyn korkeusjanan kantapiste (ei piirretty kuvaan), niin käyttämällä kahdesti pisteen potenssia kuvan kahdelle eri ympyrälle saadaan \[HN \cdot HM = HA \cdot HD = HP \cdot HQ.\]

Seuraako tästä, että \(NPMQ\) on jännenelikulmio? Eli toisin sanoen, voimmeko käyttää pisteen potenssia toiseen suuntaan? Kyllä vain: nyt pätee \[\frac{HN}{HP} = \frac{HQ}{HM},\] joten kolmiot \(HNP\) ja \(HQM\) ovat yhdenmuotoisia (sks). Täten muun muassa \(\angle NPH = \angle HMQ\), mistä väite seuraa.

Kommentti. On yleinen teema geometrian tuloksissa, että mikäli väite pätee yhteen suuntaan, niin se pätee (tarvittaessa pienin muutoksin) myös toiseen suuntaan.

Kehäkulmalause on tästä yksi hyvä esimerkki. Lause sanoo, että pisteiden ollessa ympyrän kehällä eräät kulmat ovat samat, mutta toinenkin suunta pätee: jos eräät kulmat ovat samat, niin pisteet ovat samalla ympyrällä.

Yleensä toinen suunta on helppo osoittaa soveltamalla päättelyä toiseen suuntaan (kuten yllä) tai yksikäsitteisyysargumentilla (kuten kehäkulmalauseen tapauksessa). Tämä on hyvä pitää mielessä.

24.6 Tehtäviä

Tehtävä 1. Olkoon \(ABC\) kolmio. Sovelletaan lausetta 24.2 niille ympyröille, joiden keskipisteet ovat \(A\), \(B\) ja \(C\) ja joiden säteet ovat nollia(!). Mitä tapahtuu?

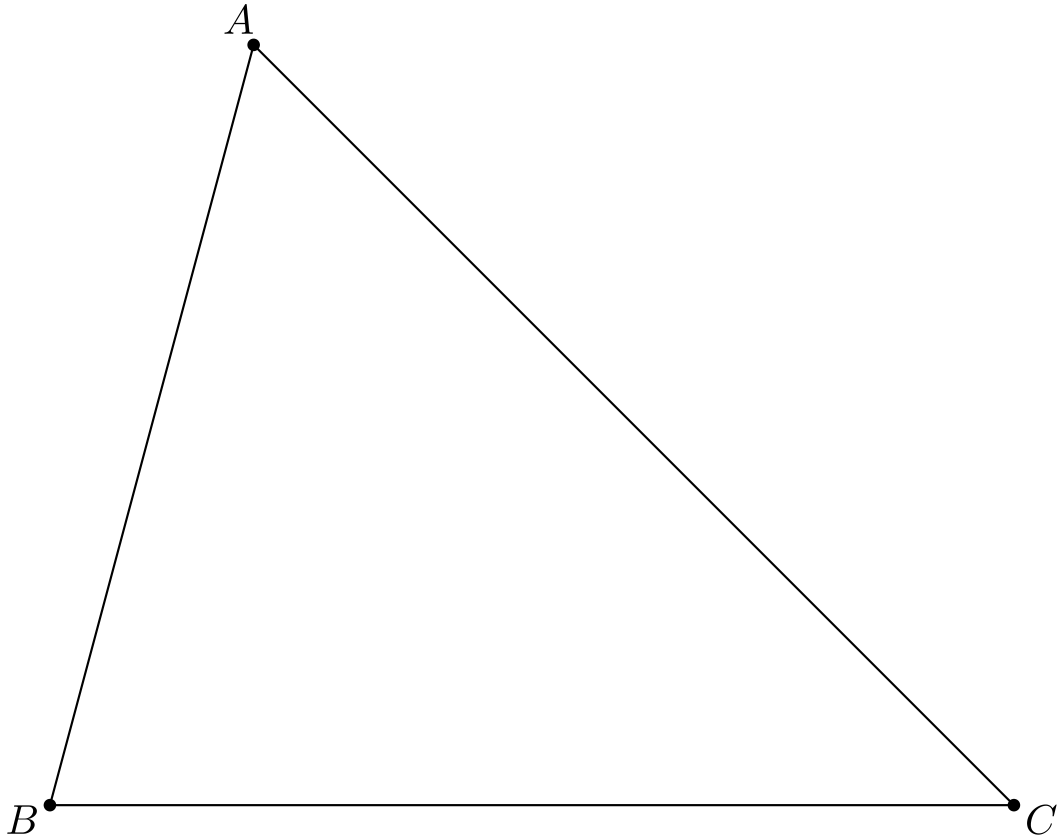
Tehtävä 2. Olkoot \(AD, BE\) ja \(CF\) kolmion \(ABC\) korkeusjanat. Sovelletaan lausetta 24.2 kolmioiden \(ABD\), \(BCE\) ja \(CAF\) ympärysympyröille. Mitä tapahtuu?

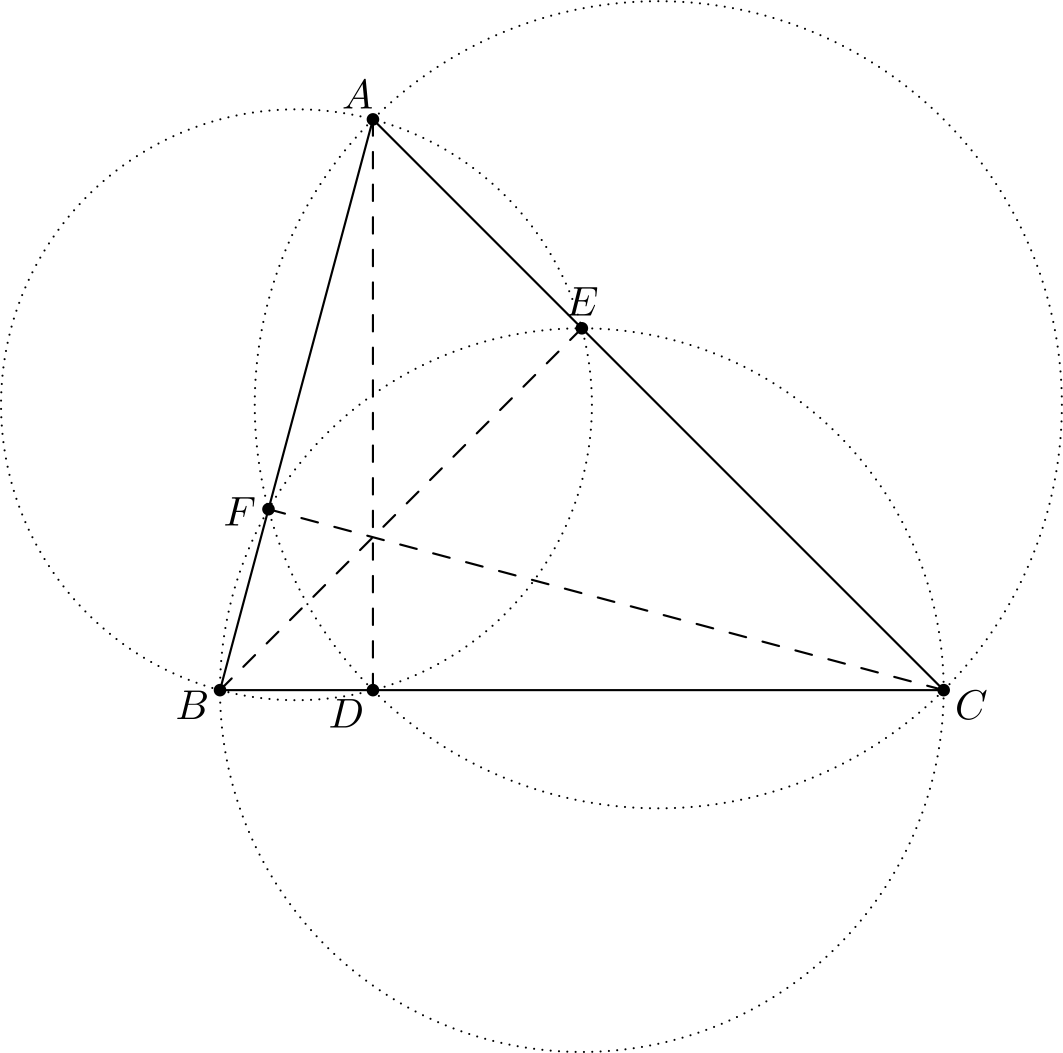
Tehtävä 3. Olkoon \(ABC\) kolmio. Olkoon \(\omega_1\) se ympyrä, joka kulkee pisteen \(A\) kautta ja joka sivuaa suoraa \(BC\) pisteessä \(B\). Olkoon \(\omega_2\) se ympyrä, joka kulkee pisteen \(A\) kautta ja joka sivuaa suoraa \(BC\) pisteessä \(C\). Olkoon \(P\) ympyröiden \(\omega_1\) ja \(\omega_2\) se leikkauspiste, joka ei ole \(A\). Olkoon \(M\) suorien \(AP\) ja \(BC\) leikkauspiste. Osoita, että \(M\) on janan \(BC\) keskipiste.

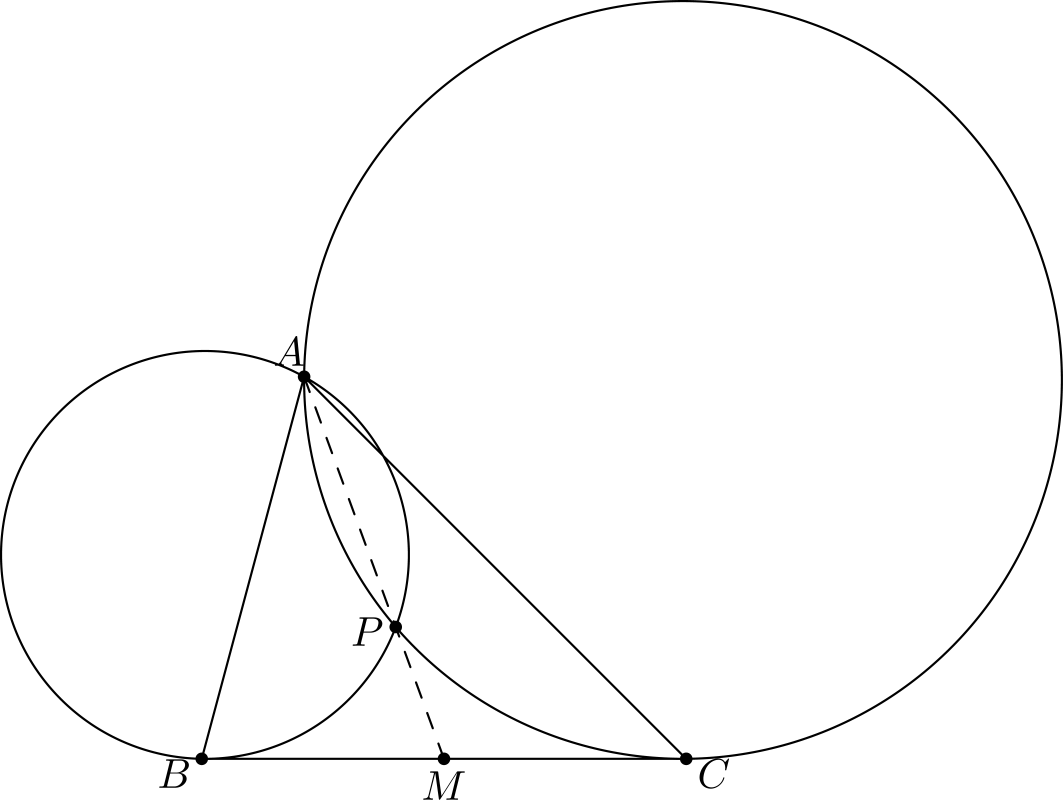
Tehtävä 4. Olkoon \(ABC\) kolmio. Piste \(D\) valitaan sivulta \(BC\). Kolmion \(ABC\) ympärysympyrälle piirretään tangentti pisteeseen \(A\) ja tangentilta valitaan piste \(E\), jolla \(DE\) ja \(AB\) ovat yhdensuuntaisia. Jana \(CE\) leikkaa kolmion \(ABC\) ympärysympyrän pisteessä \(F\). Oletetaan, että \(BDFE\) on jännenelikulmio. Osoita, että \(AC\), \(BF\) ja \(DE\) leikkaavat samassa pisteessä.

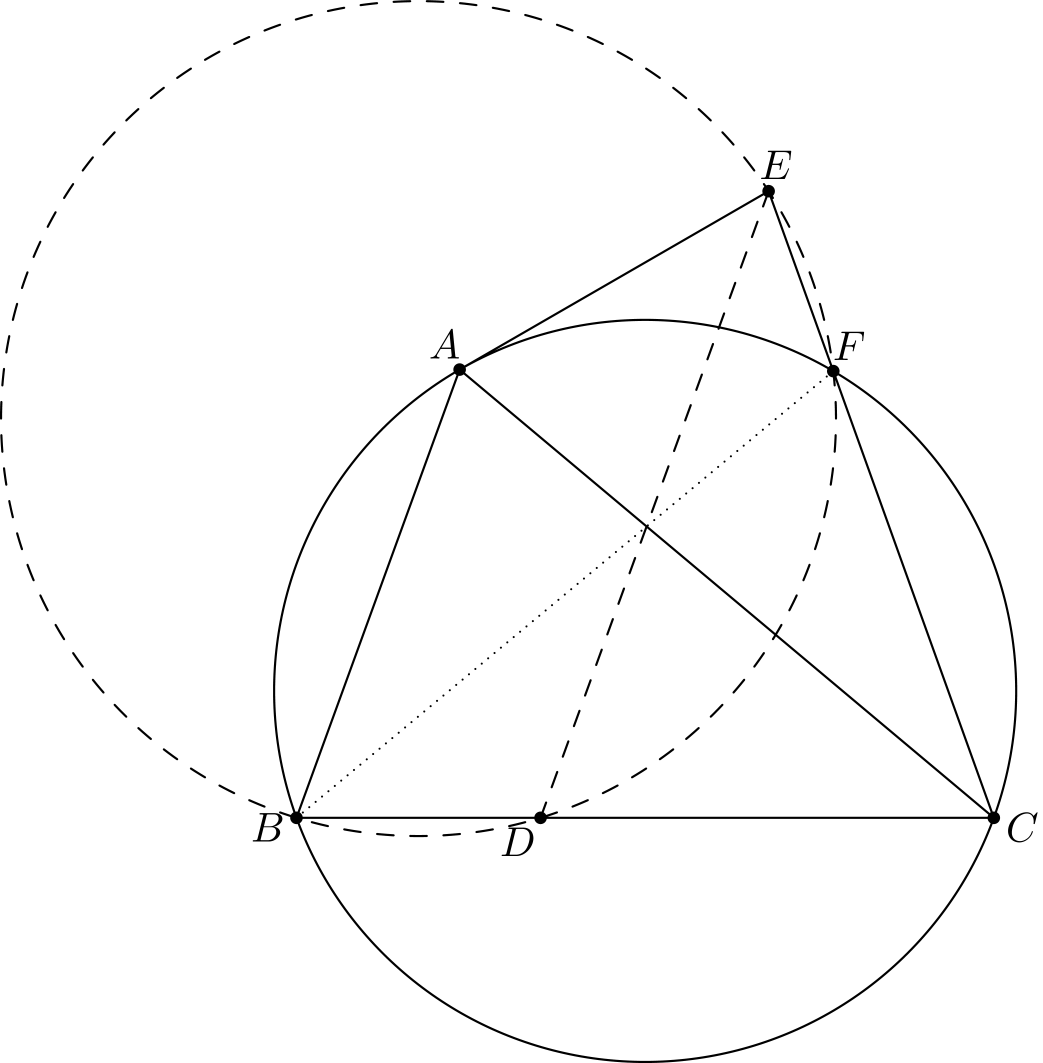
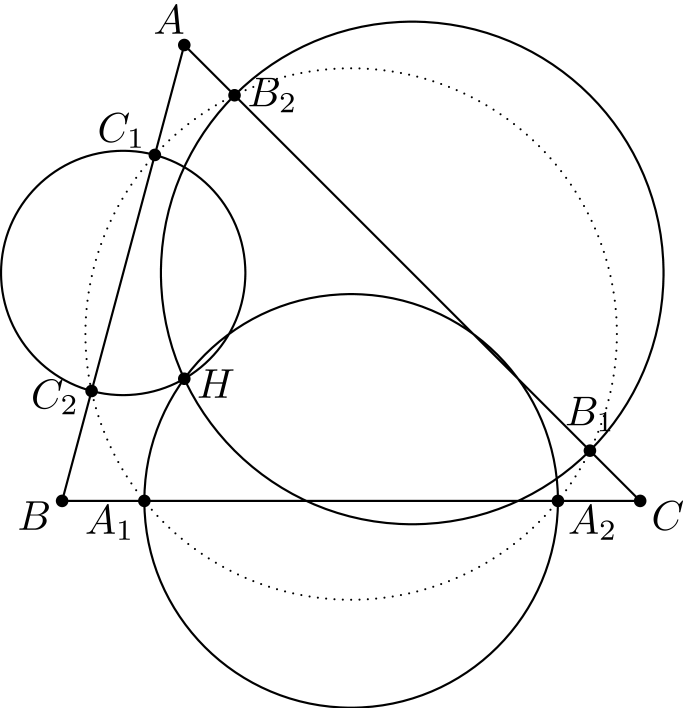
Tehtävä 5. Olkoon \(H\) teräväkulmaisen kolmion \(ABC\) ortokeskus. Ympyrä, jonka keskipiste on janan \(BC\) keskipiste ja joka kulkee pisteen \(H\) kautta, leikkaa janaa \(BC\) pisteissä \(A_1\) ja \(A_2\). Pisteet \(B_1, B_2, C_1\) ja \(C_2\) määritellään vastaavasti. Osoita, että \(A_1, A_2, B_1, B_2, C_1\) ja \(C_2\) ovat samalla ympyrällä.