10 Pituusgeometriaa

Tekijä

Olli Järviniemi

10.1 Johdanto

Tähän mennessä geometrian materiaali on keskittynyt kulmien laskemiseen. Pituudksia on käytetty ainoastaan päättelemään, että tasakylkisen kolmion kantakulmat ovat yhtä suuret. Tässä tekstissä käsitellään geometriaa vahvemmin pituuksien näkökulmasta.

10.2 Työkaluja

Tässä listataan työkalut, jotka kattavat tässä tekstissä ja monissa tehtävissä tarvittavat menetelmät. Työkalujen hyödyllisyyttä demonstroidaan alla esimerkkitehtävien kautta.

Huomaa, että monet työkalut vaativat jotakin tietoa kulmista. Eli vaikka tekstin teemana on pituudet, ei kulmiakaan saa unohtaa.

Pythagoraan lause. Suorakulmaisessa kolmiossa pätee \(a^2 + b^2 = c^2\), missä \(a\) ja \(b\) ovat kateettien pituudet ja \(c\) on hypotenuusan pituus.

Yhdenmuotoiset kolmiot. Yhdenmuotoisuussääntöjä on monia, tässä esitetään kaksi tärkeintä. Säännöt ovat käteviä, kun halutaan saada kulmaehdoista irti pituusehtoja tai päinvastoin.

Kulma-kulma (kk): Jos kahdessa kolmiossa on kaksi paria yhtä suuria kulmia, ovat kolmiot yhdenmuotoisia. Kahden kulmaparin tuntemisesta saadaan näin kolmannet kulmat ja tietoa sivujen pituuksien suhteista.

Sivu-kulma-sivu (sks): Janojen \(AB\) ja \(AC\) pituudet sekä kulma \(\angle BAC\) määräävät kolmion \(ABC\) yksikäsitteisesti. Tästä saadaan vastaava yhdenmuotoisuussääntö. Kahden sivun ja yhden kulman avulla saadaan siis loput kulmat ja kolmas sivu.

Trigonometria suorakulmaisessa kolmiossa. Suorakulmaisessa kolmiossa kaikkien kulmien ollessa tiedossa saadaan sivuja esitettyä toistensa avulla sinien, kosinien ja tangenttien avulla. Tämä on tärkeä erikoistapaus yhdenmuotoisista kolmioista.

10.3 Esimerkkitehtäviä

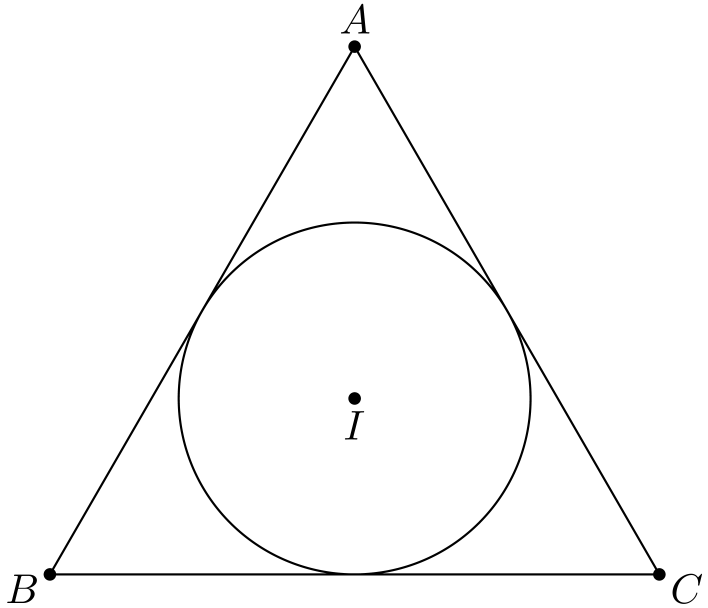
Tehtävä 10.1 Tasasivuisen kolmion \(ABC\) sivun pituus on \(2\). Laske kolmion \(ABC\) sisäympyrän säde.

Laske tasasivuisen kolmion sisäympyrän säde.

Olemme jo aiemmin (tehtävien kautta) käsitelleet joitakin kolmion sisäympyrän ominaisuuksia. Sisäympyrän keskipiste on kolmion kulmanpuolittajien leikkauspiste. Tasasivuisen kolmion tapaus on selvä: \(I\) on kolmion ”keskellä”.

Laskemista varten kuvioon tehdään joitain lisäyksiä:

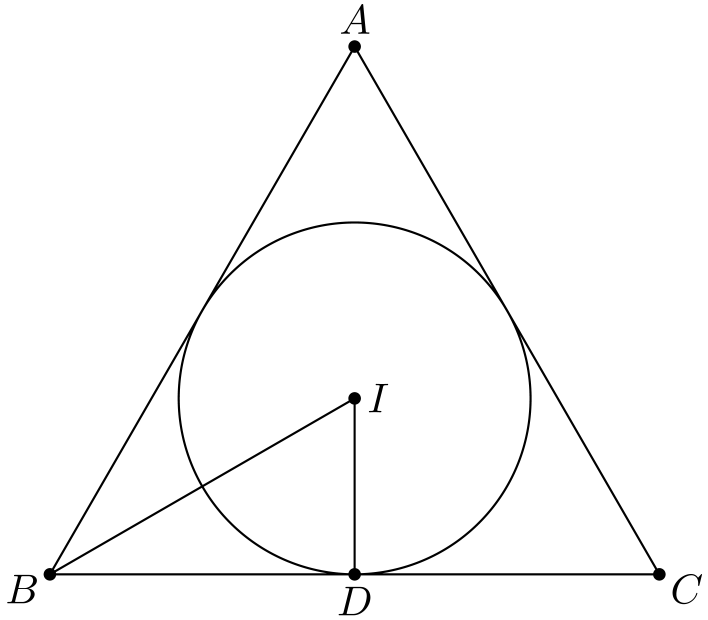
Piste \(D\) on sivun \(BC\) keskipiste ja samalla sisäympyrän sivuamispiste sivun \(BC\) kanssa. Tangentti on kohtisuorassa vastaavaa sädettä kohtaan (symmetrian vuoksi), eli kuviossa \(\angle IDB = 90^{\circ}\).

Kolmio \(BDI\) on siis suorakulmainen. Lisäksi tiedetään \(BD = 1\). Vielä tarvitaan yksi tieto, jotta kolmio määräytyy yksikäsitteisesti. Tämä tieto on \(\angle DBI\): jana \(BI\) puolittaa kulman \(\angle CBA\), joten \(\angle DBI = 60^{\circ}/2 = 30^{\circ}\).

Nyt saadaan suorakulmaisen kolmion trigonometrialla \[\tan(30^{\circ}) = \frac{ID}{BD} = ID.\] Vastaus saadaan laskimellakin, mutta \(30^{\circ}\) on ”helppo” kulma, jonka sini, kosini ja tangentti osataan laskea myös käsin. Huomataan nimittäin, että myös kolmio \(ABD\) on suorakulmainen kolmio, jonka yksi kulma on \(30^{\circ}\). Toisaalta kolmiosta \(ABD\) tiedetään \(BD = 1, AB = 2\) ja Pythagoraan lauseella \(AD = \sqrt{3}\), joten \[\tan(30^{\circ}) = \frac{BD}{AD} = \frac{1}{\sqrt{3}}.\]

Täten \(ID\) on pituudeltaan \(1/\sqrt{3}\), eli sisäympyrän säde on \(1/\sqrt{3}\).

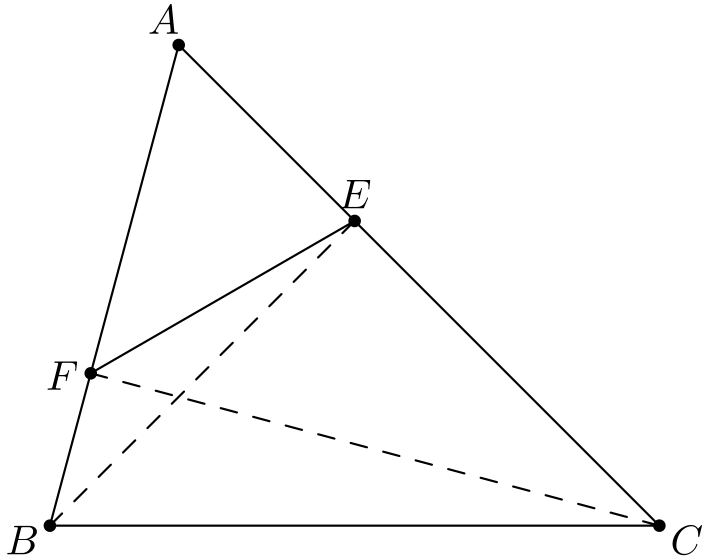
Tehtävä 10.2 Suorakulmion \(ADEH\) sivun pituudet ovat \(AD = 3\) ja \(DE = 1\). Suorakulmio jaetaan kolmeen neliöön \(ABGH\), \(BCFG\) ja \(CDEF\). Osoita, että \(\angle DAE + \angle DBE = \angle DCE\).

Osoita, että kahden pienimmän kulman summa on yhtä suuri kuin kolmas kulma.

Huomataan, että \(CDE\) on tasakylkinen suorakulmainen kolmio, joten \(\angle DCE = 45^{\circ}\). Yksi halutuista kulmista siis tiedetään.

Luonnollinen lähestymistapa on yrittää laskea muitakin kulmia ja yrittää esittää eri tuntemattomia kulmia toistensa avulla toivoen, että syntyvistä yhtälöistä saisi ratkaistua kulmat. (Tämä on strategia, mitä erityisesti moni aloittelija voisi ensimmäisenä yrittää.) Houkuttelevuudestaan huolimatta tämä etenemistapa ei oikein johda mihinkään.

Pointti on, että vaikka tehtävässä kysytään kulmia koskevaa tulosta, on kuviossa oikeasti kyse pituuksista. Kuviosta nimittäin tiedetään minkä tahansa kahden (kuvioon nimetyn) pisteen välinen etäisyys Pythagoraan lauseella.

Miten saamme muutettua pituustietoja kulmatiedoiksi? Listatuista työkaluista yhdenmuotoiset kolmiot on se, jonka avulla tämä onnistuu. Ei ole kuitenkaan selvää, miten yhdenmuotoisia kolmioita hyödynnetään.

Halutun kulmaehdon kirjoittaminen hieman eri muotoon auttaa: Huomataan, että annettu ehto pätee täsmälleen silloin, kun \(\angle DAE = \angle CEB\), koska kolmiossa \(BEC\) kulma \(\angle ECB\) on \(135^{\circ}\) ja täten \(\angle CBE + \angle BEC = 45^{\circ}\).

Ja nyt tiedämme, mistä päin kuviota yhdenmuotoisten kolmioiden pitäisi löytyä.

Väite. Kolmiot \(CBE\) ja \(CEA\) ovat yhdenmuotoisia.

Väitteen todistus. Käytetään sks-sääntöä. Molemmissa kolmioissa on \(135\) asteen kulma kärjessä \(C\). Lisäksi Pythagoraan lauseen nojalla \(CE = \sqrt{2}\), joten \[\frac{CE}{CB} = \sqrt{2}\] ja \[\frac{CA}{CE} = \frac{2}{\sqrt{2}} = \sqrt{2}.\] Sivujen suhteet ovat samat, joten sks-säännön nojalla väite pätee.

Todistuksen viimeistely. Väitteen nojalla \(\angle CAE = \angle BEC\), ja kolmiosta \(BEC\) saadaan \(\angle BEC + \angle CBE = 45^{\circ}\), mikä on haluttu väite.

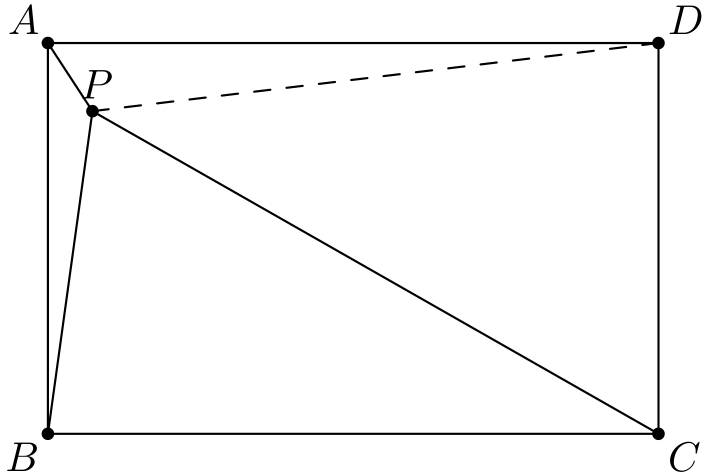
Tehtävä 10.3 Piste \(P\) on suorakulmion \(ABCD\) sisällä. Tiedetään, että \(PA = 1\), \(PB = 4\) ja \(PC = 8\). Laske \(PD\).

\(PA, PB\) ja \(PC\) tiedetään, laske \(PD\).

Ongelma vaikuttaa aika vaikealta. Emme tiedä paljoa: tiedämme, että \(ABCD\) on suorakulmio ja tiedämme kolmen janan \(PA, PB\) ja \(PC\) pituudet. Kulmatietoja ei ole (suorakulmion \(90\) asteen kulmia lukuun ottamatta).

Pienellä mielikuvituksella tajutaan piirtää pisteen \(P\) korkeusjanat sivuille \(A, B, C\) ja \(D\). Tätä kautta päästään hyödyntämään suoria kulmia.

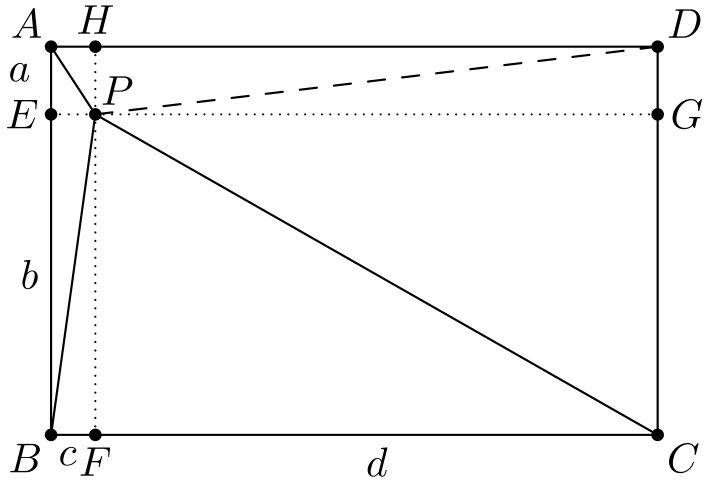
Pythagoraan lause alkaa vaikuttaa hyvältä: suoria kulmia on paljon ja myös yhtä suuria pituuksia löytyy. Merkitään yksinkertaisuuden vuoksi \(AE = a, BE = b, BF = c\) ja \(FC = d\). Huomataan, että vastakkaisilla sivuilla on yhtä pitkiä janoja, esimerkiksi \(DG = a\) ja \(PG = d\).

Pituus \(PD\) on Pythagoraan lauseen nojalla \(\sqrt{a^2 + d^2}\), eli haluamme selvittää, mitä on \(a^2 + d^2\). Mitä tiedämme luvuista \(a, b, c\) ja \(d\)? Käyttämällä Pythagoraan lausetta kolmioihin, joiden hypotenuusat ovat \(PA, PB\) ja \(PC\), saadaan \[a^2 + c^2 = 1^2,\] \[b^2 + c^2 = 4^2\] ja \[b^2 + d^2 = 8^2.\]

Huomataan, että tästä yhtälöryhmästä saadaan ratkaistua, mitä on \(a^2 + d^2\). Ensimmäisestä ja kolmannesta yhtälöstä saadaan nimittäin ratkaistua \(a^2\) ja \(d^2\): \[a^2 = 1^2 - c^2,\] \[d^2 = 8^2 - b^2,\] ja nyt \[a^2 + d^2 = 1^2 + 8^2 - (b^2 + c^2) = 1^2 + 8^2 - 4^2 = 49,\] missä käytettiin vielä toista yhtälöä. Täten \[PD = \sqrt{a^2 + d^2} = 7,\] eli haluttu pituus on \(7\).

Kommentti. Luvuilla \(1, 4\) ja \(8\) ei ollut mitään erityistä virkaa, vaan sama lasku toimii millä tahansa luvuilla: aina pätee \(PA^2 + PC^2 = PB^2 + PD^2\). Sivun \(PD\) pituus ei kuitenkaan välttämättä ole kokonaisluku, vaikka pituudet \(PA, PB\) ja \(PC\) olisivat.

10.4 Tehtäviä

Tehtävä 1. Neliön sisällä on kuvan mukaisesti kaksi ympyrää, joiden kummankin säde on \(1\). Laske neliön sivun pituus.

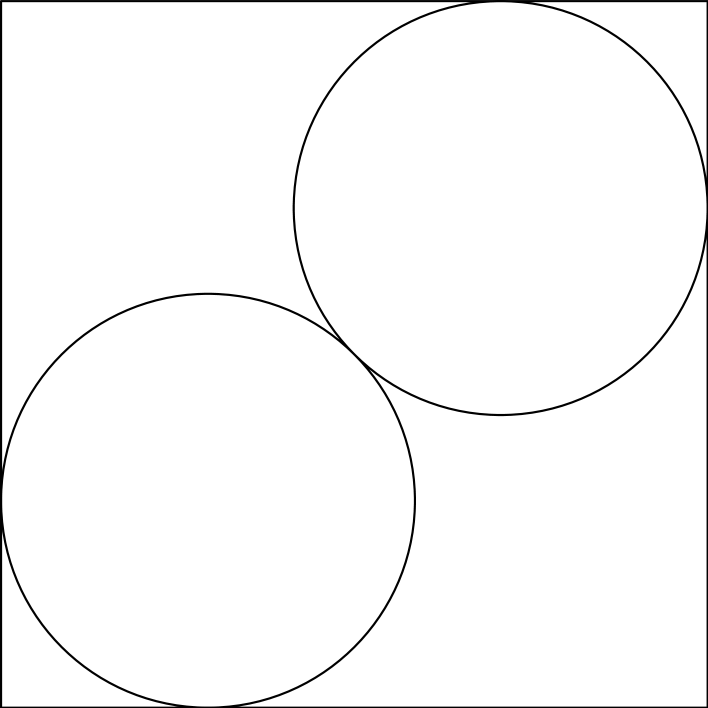
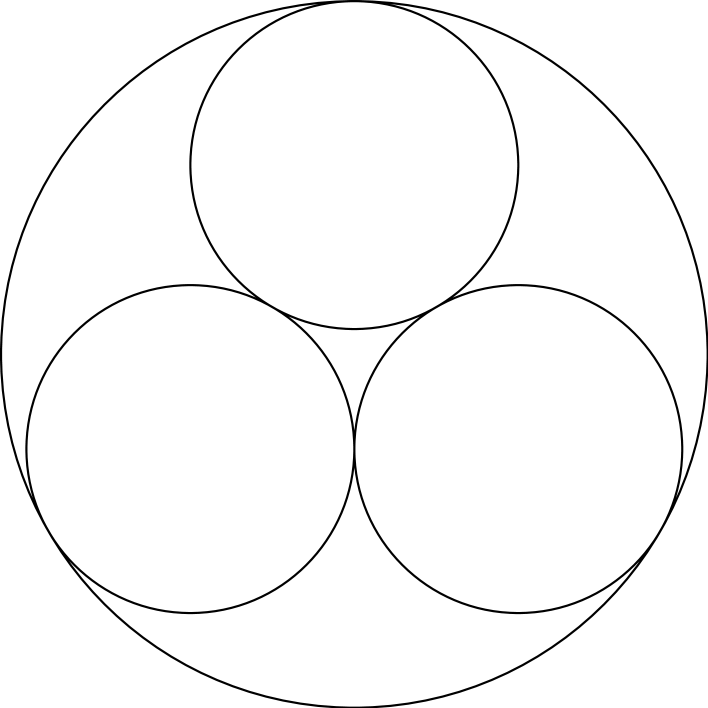
Tehtävä 2. Ympyrän sisällä on kolme pienempää ympyrää kuvan mukaisesti. Pienien ympyröiden säteet ovat \(1\). Laske suuren ympyrän säde.

Tehtävä 3. Piste \(P\) on ympyrän ulkopuolella. Pisteestä \(P\) piirretään kaksi suoraa, jotka leikkaavat ympyrän pisteissä \(A\) ja \(B\) sekä \(C\) ja \(D\). Osoita, että \(PA \cdot PB = PC \cdot PD\).

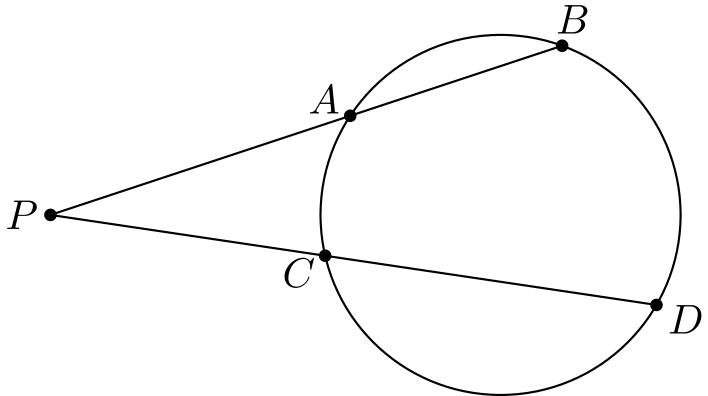
(Tätä tulosta kutsutaan pisteen potenssiksi. Siihen keskitytään tarkemmin myöhemmässä geometrian tekstissä. Vastaava tulos pätee myös, jos \(P\) on ympyrän sisällä.)

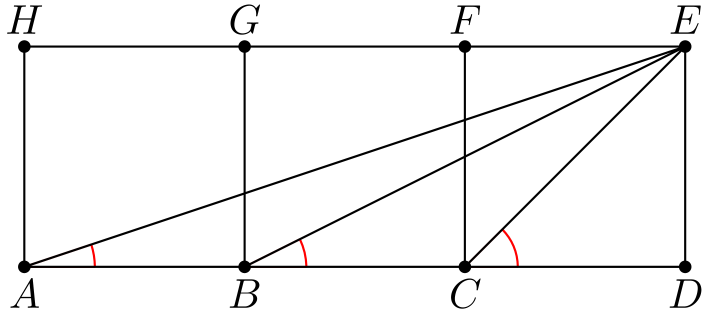
Tehtävä 4. Pisteet \(E\) ja \(F\) ovat kolmion \(ABC\) sivujen \(AC\) ja \(AB\) keskipisteet. Osoita, että \(\angle EFA = \angle CBA\).

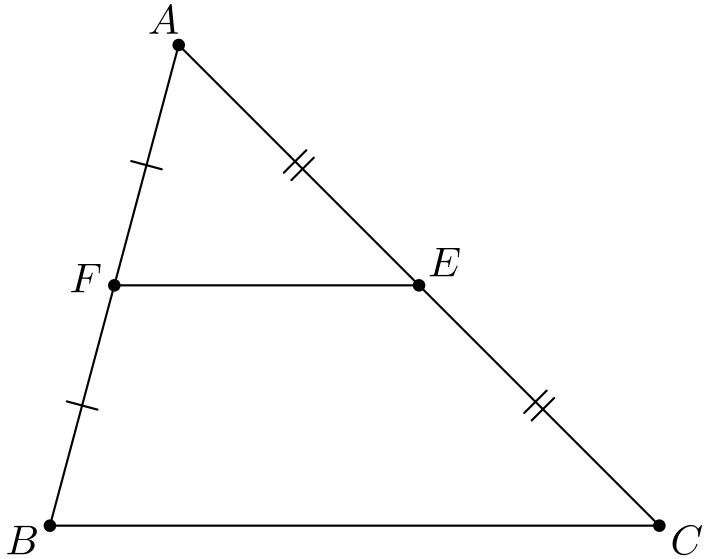
Tehtävä 5. Piste \(M\) on kolmion \(ABC\) sivun \(BC\) keskipiste ja piste \(K\) on sivun \(AC\) keskipiste. Olkoon \(G\) janojen \(AM\) ja \(BK\) leikkauspiste. Osoita, että \[\frac{AG}{GM} = 2.\]

Huomautus:

Janaa \(AM\) kutsutaan kolmion \(ABC\) kärjestä \(A\) piirretyksi mediaaniksi tai lyhyesti \(A\)-mediaaniksi. Tehtävän tulos sanoo, että \(B\)-mediaani jakaa \(A\)-mediaanin osiin, joiden suhde on \(2 : 1\). Vastaavasti myös \(C\)-mediaani jakaa \(A\)-mediaanin suhteessa \(2 : 1\). Täten \(B\)- ja \(C\)-mediaanit molemmat leikkaavat \(A\)-mediaanin samassa pisteessä, joka on tehtävän piste \(G\). Pistettä \(G\) kutsutaan kolmion \(ABC\) mediaanien leikkauspisteeksi tai painopisteeksi.

Olemme nyt saaneet esiteltyä kolmion neljä tärkeintä pistettä. Nämä ovat keskinormaalien leikkauspisteessä sijaitseva ympärysympyrän keskipiste \(O\), korkeusjanojen leikkauspiste eli ortokeskus \(H\), kulmanpuolittajien leikkauspisteessä sijaitseva sisäympyrän keskipiste \(I\) ja mediaanien leikkauspiste eli painopiste \(G\).

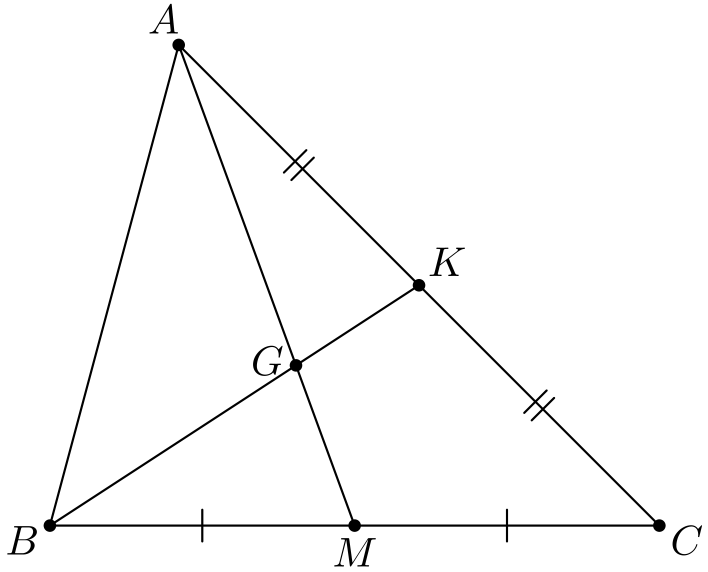
Tehtävä 6. Janat \(BE\) ja \(CF\) ovat (teräväkulmaisen) kolmion \(ABC\) korkeusjanoja. Osoita, että \(EF = BC \cdot \cos(\angle BAC)\).