28 Transformaatiot

Tekijä

Olli Järviniemi

28.1 Johdanto

Tässä tekstissä käsitellään geometristen transformaatioiden hyödyntämistä geometrian tehtävissä. Ideoissa ei ole sinänsä mitään uutta – loppukädessä kaikki palautuu yhdenmuotoisiin kolmioihin, jotka ovat tuttuja. Tämä on kuitenkin hieman erilainen tapa katsoa geometrian kuvioita, ja tämä tapa on monesti hyödyllinen.

28.2 Peilaukset

Peilaukset ovat luonnostaan nousseet esiin tutkiessamme ortokeskuksia: kolmion \(ABC\) ortokeskuksen peilaus sivun \(BC\) yli sijaitsee kolmion \(ABC\) ympärysympyrällä. Me oikeastaan todistimme ortokeskuksen olemassaolon tätä kautta. Tässä on vielä toinen ortokeskukseen liittyvä peilausominaisuus.

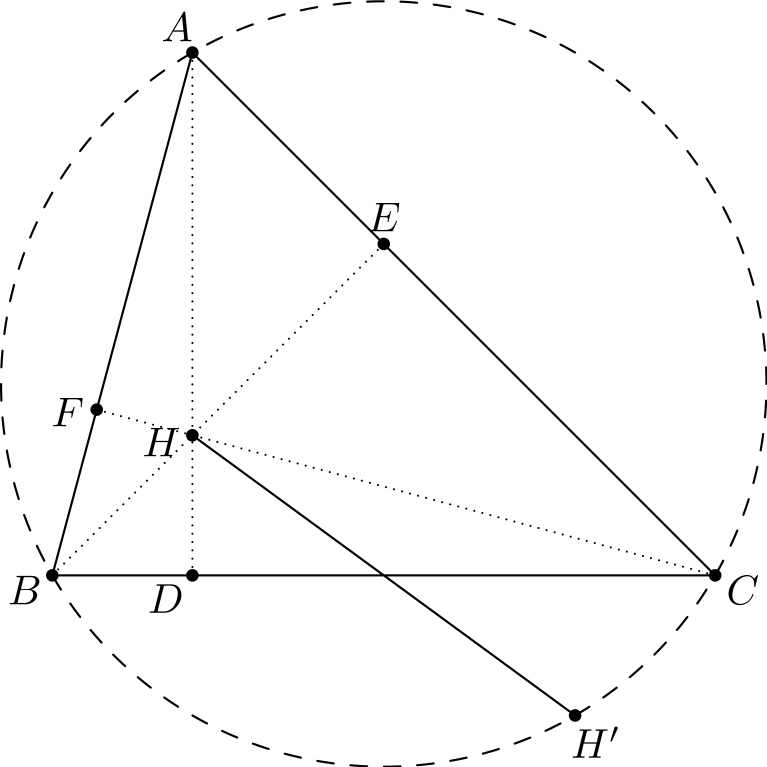
Tehtävä 28.1 Olkoon \(ABC\) kolmio ja olkoon \(H\) sen ortokeskus. Olkoon \(H'\) pisteen \(H\) peilaus sivun \(BC\) keskipisteen yli. Osoita, että \(AH'\) on kolmion \(ABC\) ympärysympyrän halkaisija.

Kolmion ortokeskus ja sen peilaus sivun keskipisteen yli.

Kuvaan on lisätty korkeusjanat ja niiden kantapisteet, koska ne auttavat kuvion hahmottamisessa ja kulmanjahtauksessa.

Yritetään ensiksi todistaa, että \(H'\) on ympärysympyrällä. Tämän todistamiseksi lienee helpointa osoittaa, että \(\angle CH'B + \angle A = 180^{\circ}\). Mutta tämä on helppoa: \[\angle CH'B = \angle BHC = \angle EHF = 180^{\circ} - \angle A,\] missä käytimme peilausominaisuutta ja sitä tietoa, että \(AFHE\) on jännenelikulmio.

Todistetaan sitten, että \(AH'\) on ympyrän halkaisija. Tätä varten osoitetaan, että \(\angle H'BA = 90^{\circ}\). Käyttämällä peilausominaisuutta saadaan \[\angle H'BC = \angle HCB = \angle FCB = 90^{\circ} - \angle B,\] missä viimeisessä askeleessa hyödynnetään suorakulmaista kolmiota \(BFC\). Väite seuraa tästä.

Tämä oli melko suoraviivainen esimerkki: peilaus toimi vain tapana saada yhtä suuria kulmia. Seuraavassa vaikeammassa esimerkissä peilaukset toimivat työkaluna hankalien pituusehtojen käsittelemisessä.

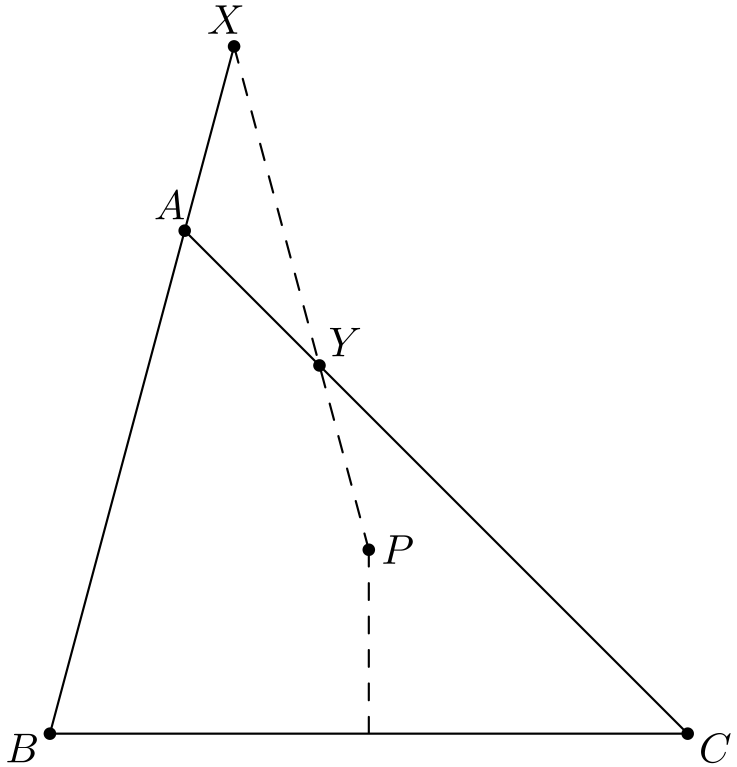
Tehtävä 28.2 Olkoon \(ABC\) kolmio, jossa \(AC > AB\). Piste \(X\) sijaitsee suoralla \(AB\) niin, että \(B\) ja \(X\) ovat eri puolilla pistettä \(A\) ja \(BX = CA\). Piste \(Y\) sijaitsee janalla \(AC\) niin, että \(CY = BA\). Piste \(P\) on janan \(BC\) keskinormaalin leikkauspiste suoran \(XY\) kanssa. Osoita, että \(\angle BPC + \angle BAC = 180^{\circ}\).

Kolmio \(ABC\) ja erikoisilla ehdoilla määriteltyjä pisteitä.

Tehtävässä on monia erikoisia piirteitä. Pisteet \(X\) ja \(Y\) ovat jo itsessään melko epätyypillisiä, puhumattakaan pisteestä \(P\). Lisäksi tehtävänannon loppu yllättää: kaikki muu viittaa siihen, että kyseessä on ”pituustehtävä”, mutta todistettava väite onkin kulmaehto.

Haluttu kulmaehto ei ole tällaisenaan kovin luonnollinen. Se kannattaa tulkita niin, että pisteen \(P\) peilaus janan \(BC\) yli on kolmion \(ABC\) ympärysympyrän kehällä.¹

¹ Ympärysympyrä näyttelee roolia, vaikkei sitä tehtävässä erikseen mainitakaan. Tämä ei ole mitenkään epätyypillistä. Tästä syystä on usein hyvä idea piirtää kolmion \(ABC\) ympärysympyrä kuvaan.

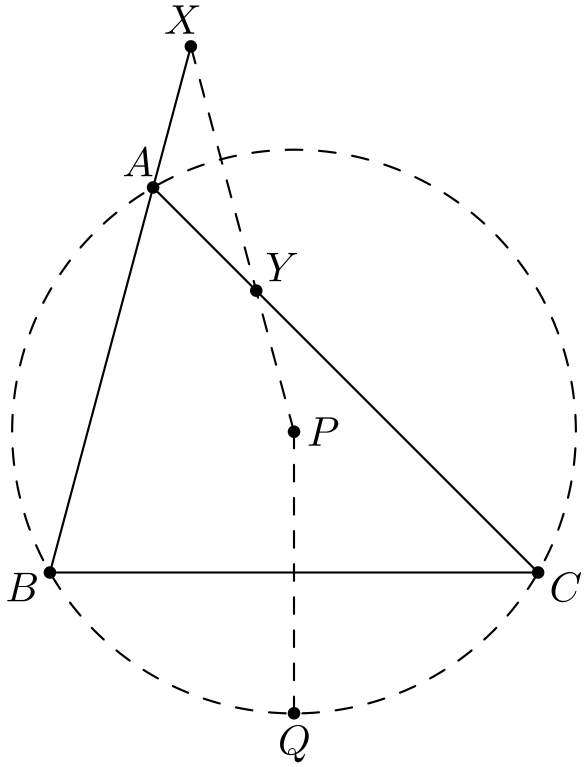
Pisteen \(P\) peilaus pisteeksi \(Q\). Haluamme osoittaa, että \(Q\) on kolmion \(ABC\) ympärysympyrällä.

Tämä auttaa hieman, mutta moni kysymys kaipaa vielä vastausta. Mitä pisteet \(X\) ja \(Y\) ”ovat”? Ja miten ne liittyvät pisteeseen \(Q\)? Miten saamme muutettua pituusehdot kulmaehdoiksi?

Olemme jo peilanneet pisteen \(Q\). On luontevaa peilata myös pisteet \(X\) ja \(Y\), yrityksenä saada yhdistettyä pisteet \(X\) ja \(Y\) pisteeseen \(Q\). Yksi luonteva idea on peilata \(X\) ja \(Y\) suoraan sivun \(BC\) yli. On kuitenkin parempi peilata \(X\) ja \(Y\) sivun \(BC\) keskipisteen yli. Näin pituusehtoja saadaan käsiteltyä paremmin.

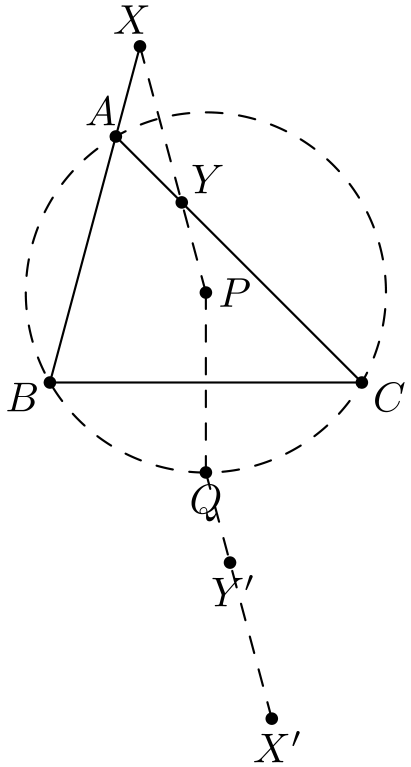
Peilataan myös pisteet \(X\) ja \(Y\). Haluamme osoittaa, että \(Q\) on kolmion \(ABC\) ympärysympyrällä.

Pari huomiota: Ensinnäkin \(BYCY'\) ja \(BXCX'\) ovat peilausominaisuuksista johtuen suunnikkaita. Toiseksi käyttämällä annettuja pituusehtoja ja suunnikasominaisuutta saadaan \[AB = CY = BY',\] eli \(ABY'\) on tasakylkinen kolmio. Vastaavasti \(ACX'\) on tasakylkinen.

Tehtävä alkaa ratkeamaan tästä. Kolmion \(BAY'\) huippukulmaksi saadaan suunnikkaita käyttämällä \[\angle Y'BA = \angle Y'BC + \angle CBA = \angle C + \angle B.\] Täten kantakulmat ovat \(\angle A/2\). Erityisesti \(\angle BAY' = \angle A/2\), eli \(Y'\) on kulman \(\angle BAC\) kulmanpuolittajalla. Vastaavasti myös \(X'\) on tällä kulmanpuolittajalla. Tämä tarkoittaa, että pisteet \(A, X', Y'\) ja siten myös \(Q\) ovat kaikki samalla suoralla.

Siis \(Q\) on kolmion \(ABC\) kärjestä \(A\) piirretyn kulmanpuolittajan leikkauspiste sivun \(BC\) keskinormaalin kanssa. Toisaalta tiedetään, että jos \(M\) on kolmion \(ABC\) ympärysympyrän kaaren \(BC\) keskipiste, niin se on tällä kulmanpuolittajalla ja keskinormaalilla. Täten \(Q\) ja \(M\) ovat sama piste. Siis \(Q\) on kolmion \(ABC\) ympärysympyrällä, mikä on haluttu väite.

Kommentti. Tarinan opetus: Peilauksien hyödyllisyys perustuu siihen, että niillä voi liikuttaa pisteitä ilman, että (jotkin) pituudet tai kulmat muuttuvat. Jos siis kuviossa on yhtä pitkiä janoja, jotka ovat ”kaukana toisistaan” tai ”väärissä paikoissa”, voi peilauksilla yrittää korjata tilannetta.

Kierroilla on samanlaiset ominaisuudet ja käyttökohteet. Peilaus pisteen suhteen onkin oikeastaan \(180\) asteen kierto.

28.3 Skaalaukset

Yksi tilanne, jota voi miettiä skaalausten kautta, koskee kolmion mediaaneja (joita käsiteltiin Pituusgeometriaa-tekstin tehtävissä).

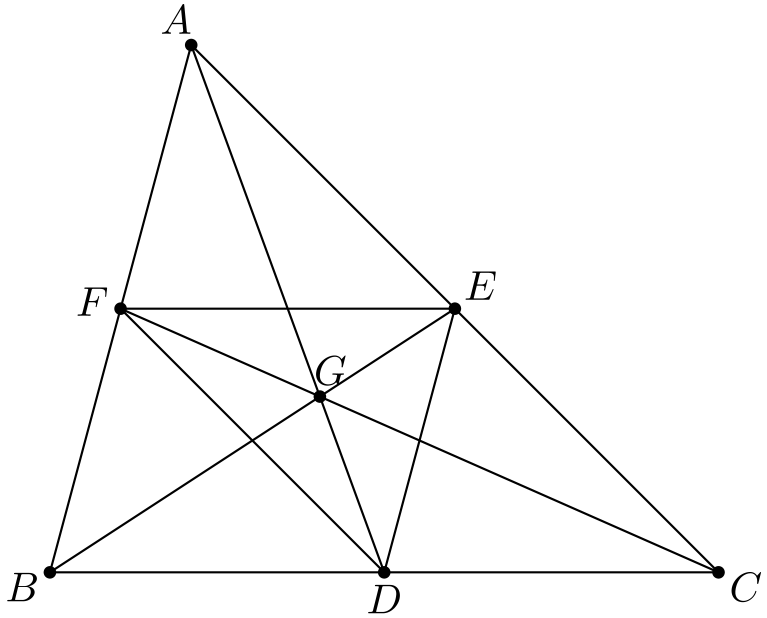
Kuviosta löytyy muutamakin skaalaus. Jos kuviota skaalataan keskipisteenä \(A\) kertoimella \(2\) kuvautuu piste \(F\) pisteeksi \(B\) ja piste \(E\) pisteeksi \(C\). Tästä seuraa, että \(FE\) ja \(BC\) ovat yhdensuuntaisia. (Kyse on vain yhdenmuotoisista kolmioista.) Jos taas tehdään skaalaus keskipisteellä \(G\) ja kertoimella \(-2\) (eli skaalataan ensin kertoimella \(2\) ja peilataan sitten pisteen \(G\) yli), niin pisteet \(D, E\) ja \(F\) kuvautuvat pisteiksi \(A, B\) ja \(C\).

Tässä tapauksessa skaalaus ei ehkä kerro mitään uutta, mutta joissain tehtävissä skaalaus on hyvä tapa ajatella tilannetta. Esitetään tästä esimerkki.

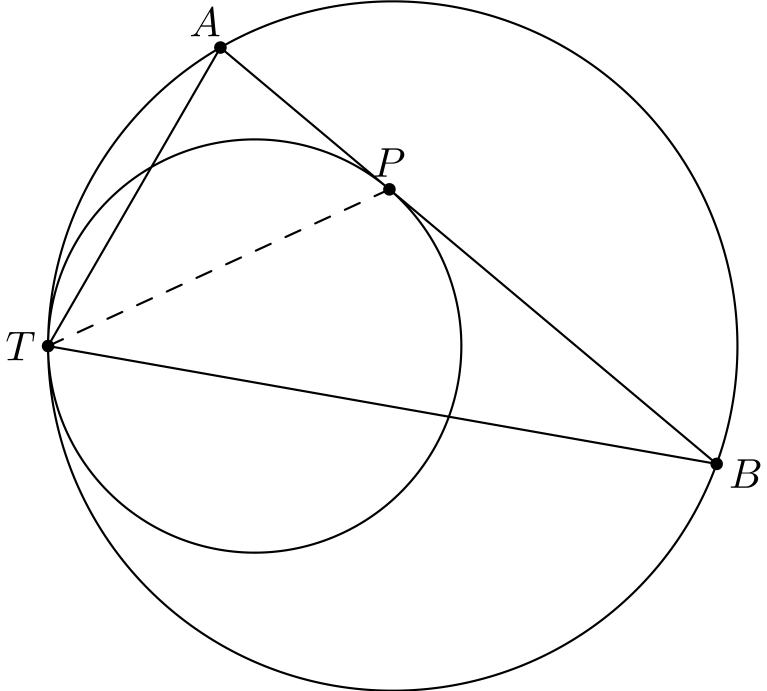
Tehtävä 28.3 Kaksi ympyrää sivuaa toisiaan sisäpuolisesti pisteessä \(T\). Ulomman ympyrän jänne \(AB\) sivuaa sisempää ympyrää pisteessä \(P\). Osoita, että suora \(TP\) puolittaa kulman \(\angle BTA\).

Sivuavia ympyröitä, tangentti ja kulmanpuolittaja.

Ajatus on, että isompi ympyrä saadaan skaalaamalla pienempää ympyrää. Tilanteen hahmottamiseksi lisätään kuvioon muutama piste.

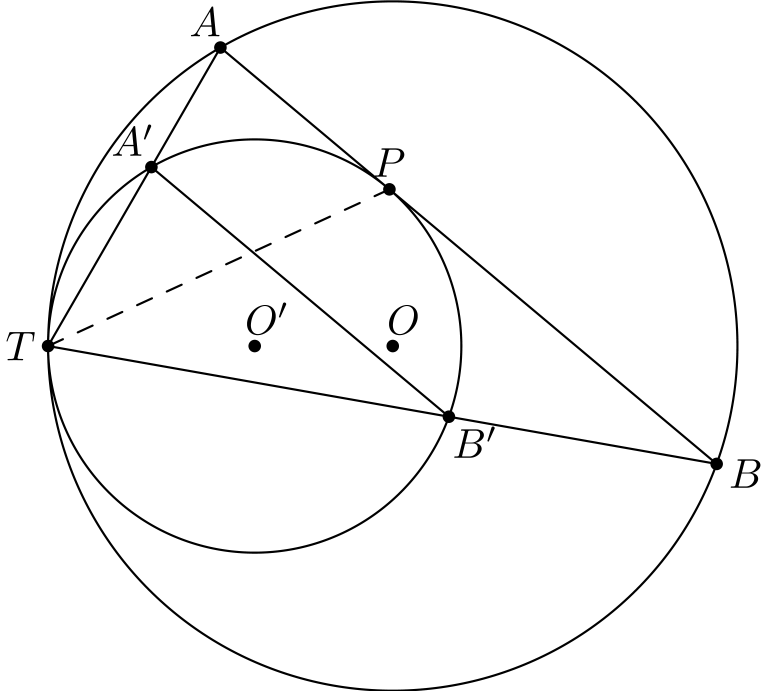
Ideana on, että skaalauksen seurauksena monet kuviosta löytyvistä kolmioista ovat yhdenmuotoisia keskenään. Tästä saadaan laskettua kulmia.

Aluksi huomataan, että \(T, O\) ja \(O'\) ovat ympyröiden sivuamisominaisuuden nojalla samalla suoralla (sekä \(TO\) että \(TO'\) ovat kohtisuorassa pisteeseen \(T\) piirrettyyn tangenttiin nähden). Tästä seuraa muun muassa, että \(TOA\) ja \(TO'A'\) ovat tasakylkisiä kolmioita, joilla on yhtä suuret kantakulmat \(\angle OTA = \angle O'TA'\), eli ne ovat yhdenmuotoisia.

Kehäkulmalauseen keskuskulmaversion nojalla nyt saadaan lisää yhtä suuria kulmia. Esimerkiksi \(AB\) ja \(A'B'\) ovat yhdensuuntaisia, koska kehäkulmalauseen keskuskulmaversiolla \[\angle A'B'T = \frac{\angle A'O'T}{2} = \frac{\angle AOT}{2} = \angle ABT.\]

Muuta emme oikeastaan tarvitsekaan. Tehtävä ratkeaa tästä käyttämällä kehäkulmalauseen tangenttiversiota ja sitten janojen \(A'B'\) ja \(AB\) yhdensuuntaisuutta: \[\angle B'A'P = \angle B'PB = \angle PB'A',\] joten kehäkulmalauseen nojalla \(\angle B'TP = \angle PTA'\).

Kommentti. Yleisesti skaalatessa jana kuvautuu sen kanssa yhdensuuntaiseksi janaksi, ja skaalatessa ympyrää on lopputuloskin ympyrä. Tämä enemmän tai vähemmän perustelee, miksi \(AB\) ja \(A'B'\) ovat yhdensuuntaisia.

28.4 Tehtäviä

Tehtävä 1. Suorakulmion \(ABCD\) sisällä on sellainen piste \(P\), että \(\angle DPA + \angle BPC = 180^{\circ}\). Osoita, että \(\angle PBA = \angle ADP\).

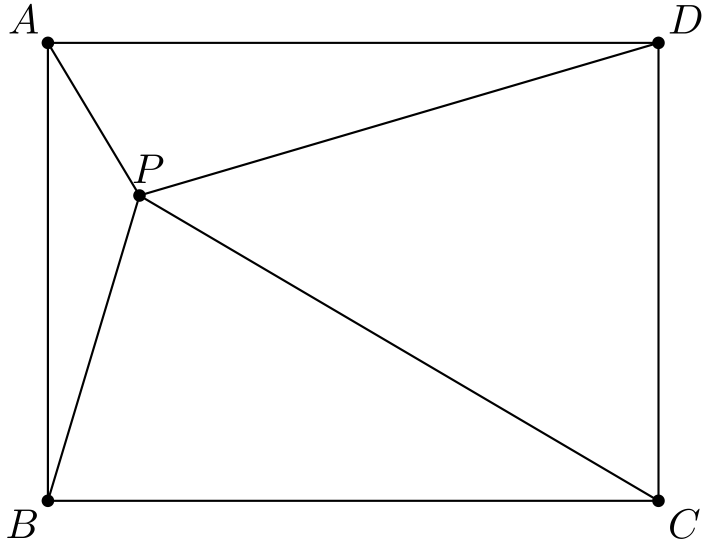
Tehtävä 2. Olkoon \(M\) kolmion \(ABC\) sivun \(BC\) keskipiste. Osoita, että \(AM \le (AB + AC)/2\).

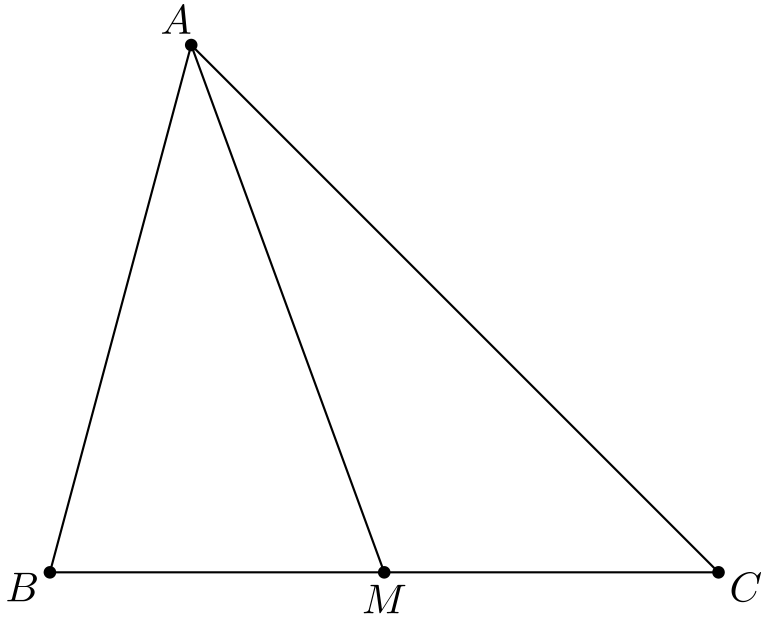
Tehtävä 3. Mitä seuraavassa kuvassa tapahtuu?

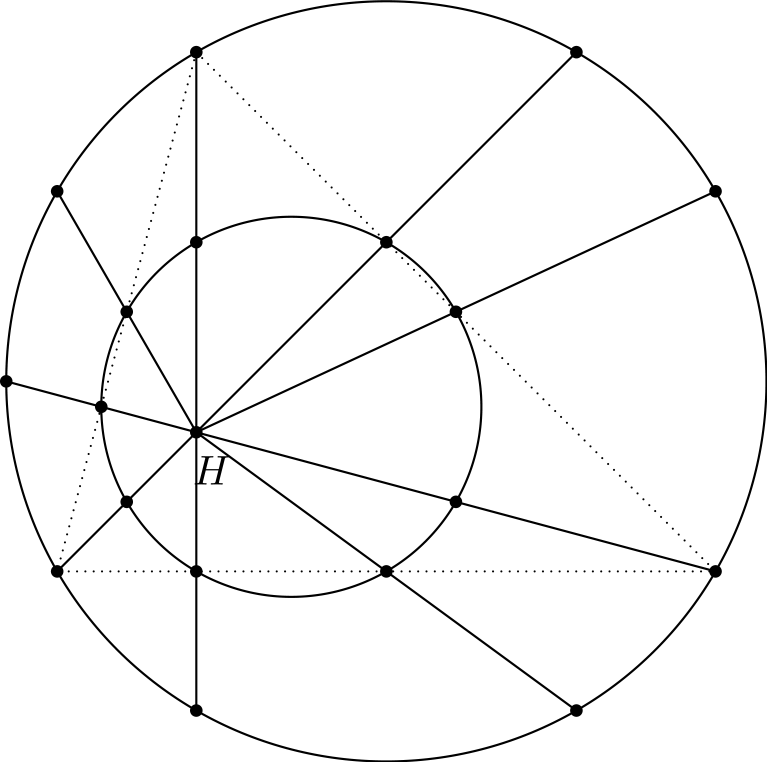
Tehtävä 4. Ympyrällä on jänne \(AB\). Piirretään pienempi ympyrä, joka on tangentti jänteelle \(AB\) pisteessä \(P\) ja ympyrälle pisteessä \(T\). Olkoon \(M\) sen kaaren \(AB\), joka ei sisällä pistettä \(T\), keskipiste. Osoita, että \(M, P\) ja \(T\) ovat samalla suoralla.

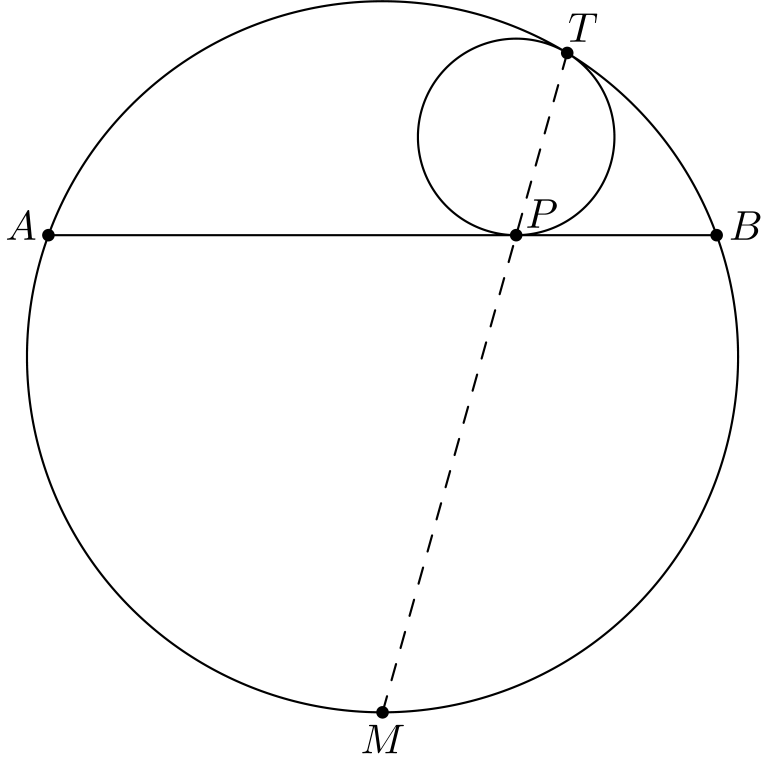
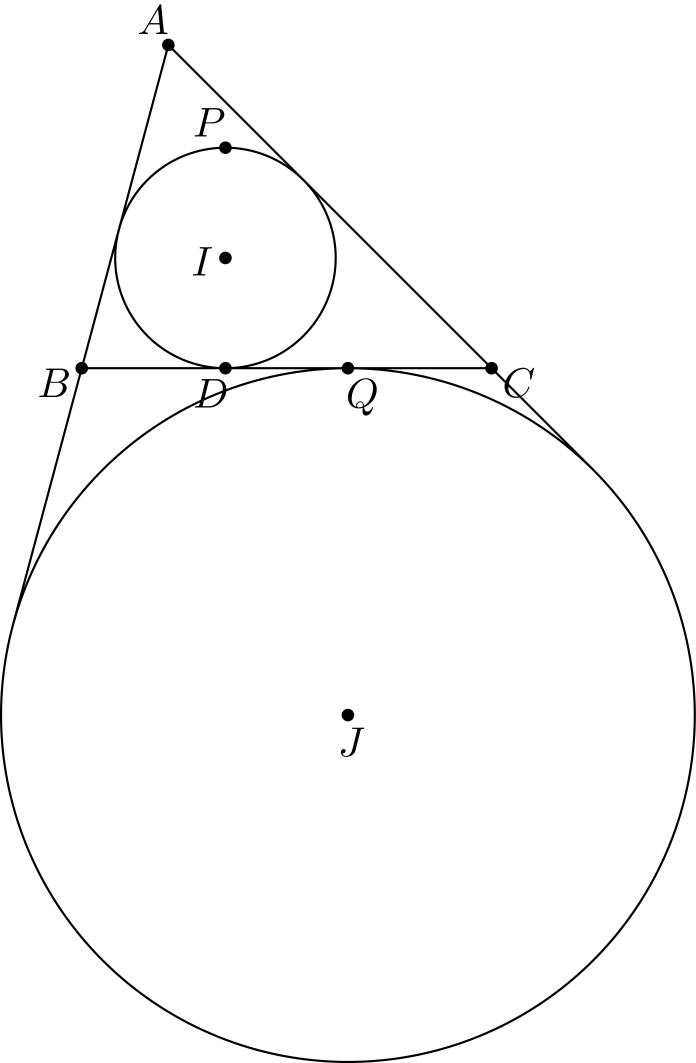
Tehtävä 5. Olkoon \(I\) kolmion \(ABC\) sisäympyrän keskipiste. Olkoon \(D\) sisäympyrän sivuamispiste sivun \(BC\) kanssa, ja olkoon \(P\) sellainen sisäympyrän piste, että \(DP\) on sisäympyrän halkaisija. Kolmion \(ABC\) kärjen \(A\) vastainen sivuympyrä sivuaa janaa \(BC\) pisteessä \(Q\). Osoita, että \(A, P\) ja \(Q\) ovat samalla suoralla.

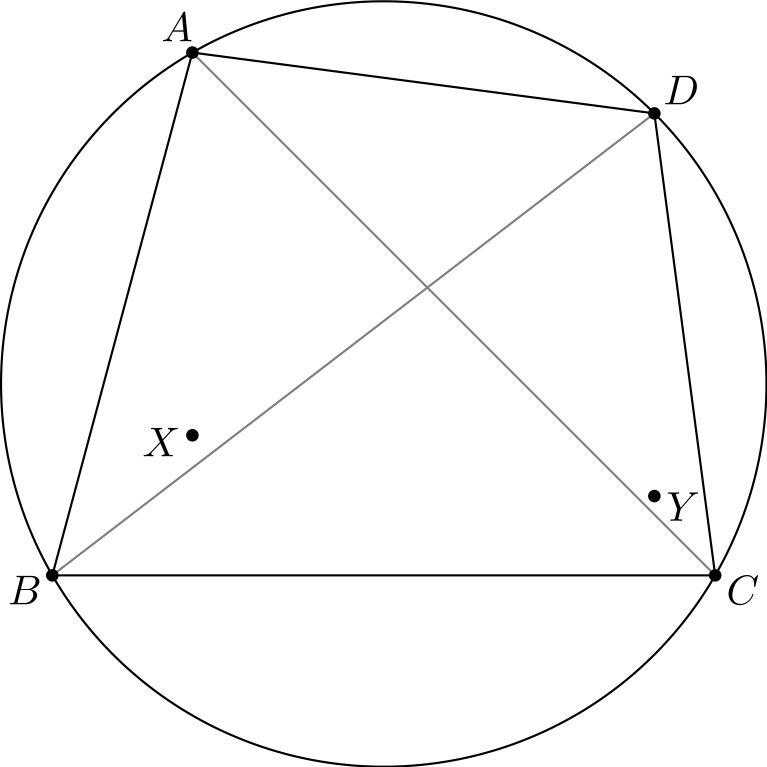
Tehtävä 6. Olkoon \(ABCD\) jännenelikulmio. Olkoot \(X\) ja \(Y\) kolmioiden \(ABC\) ja \(BCD\) ortokeskukset. Osoita, että \(AXYD\) on suunnikas.