14 Geometriset konfiguraatiot

Tekijä

Olli Järviniemi

14.1 Johdanto

Geometrian tehtävissä on tiettyjä usein toistuvia kuvioita. Esimerkiksi monen tehtävän pohjalla on kolmio ja sen sisäympyrä, ympärysympyrä tai korkeusjanoja. Yleisimmät konfiguraatiot kannattaa siis tuntea hyvin.

Joitakin konfiguraatioita on käsitelty jo aiemmissa teksteissä suoraan tai tehtävissä. Ehkäpä tärkeimmät tiedot ovat, että kolmiolla on ympärysympyrä (jonka keskipiste on sivujen keskinormaalien leikkauspiste) ja sisäympyrä (jonka keskipiste on kulmanpuolittajien leikkauspiste) ja että kolmion korkeusjanat leikkaavat samassa pisteessä. Lisäksi näillä kuvioilla on tiettyjä ominaisuuksia: esimerkiksi korkeusjanakuviosta löytyy paljon jännenelikulmioita.

Tässä tekstissä käsitellään lisää konfiguraatioita. Jotkin näistä, kuten kehäkulmalauseen tangenttiversio ja sisäympyrän ominaisuudet, ovat hyvin käyttökelpoisia jo kansallisen tason tehtävissä. Jotkut esiintyvät sellaisenaan vasta kansainvälisellä tasolla, mutta konfiguraatiot toimivat silti hyvinä harjoitustehtävinä.

Käytämme tässä tekstissä (ja myöhemminkin) lyhennysmerkintää $\angle BAC = \angle A$ kolmion $ABC$ kärjen $A$ kulmalle. Vastaavasti merkitään $\angle CBA = \angle B$ ja $\angle ACB = \angle C$ .

14.2 Kehäkulmalauseen tangenttiversio

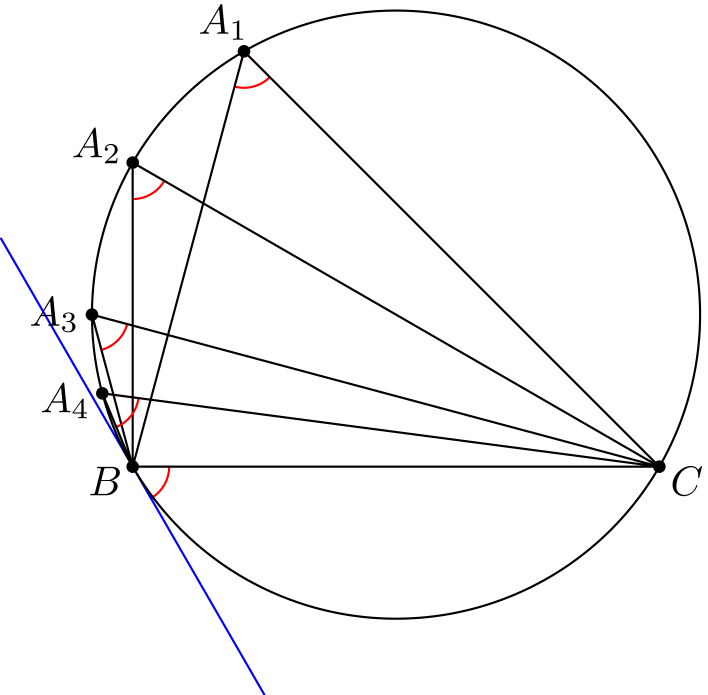
Ympyrä ja sen jänne BC. Kehän neljästä eri pisteestä A1, A2, A3 ja A4 jänteeseen BC piirretyt kehäkulmat on merkitty punaisella, ja ne ovat keskenään yhtä suuret. Sininen jana kuvaa pisteeseen B piirrettyä tangenttia, ja tangentin ja jänteen välinen kulma on sama kuin kehäkulmat. — Eräitä tapauksia kehäkulmalauseesta.

Kehäkulmalauseen nojalla tiedämme, että samaa jännettä vastaavat kehäkulmat ovat yhtä suuria, eli yllä olevassa kuvassa $\angle BA_1C = \angle BA_2C = \angle BA_3C = \angle BA_4C$ . Kun pisteet $A_i$ lähestyvät pistettä $B$ , kulma $\angle BA_iC$ alkaa näyttää enemmän ja enemmän jänteen $BC$ ja pisteeseen $B$ piirretyn ympyrän tangentin väliseltä kulmalta.

Kulmat todella ovat yhtä suuria. Tätä kutsutaan kehäkulmalauseen tangenttiversioksi.

Lause 14.1 (Kehäkulmalauseen tangenttiversio) Olkoon $ABC$ kolmio ja olkoon $D$ piste, joka on eri puolella suoraa $BC$ kuin piste $A$ ja jolla $BD$ on tangentti kolmion $ABC$ ympärysympyrälle. Tällöin $\angle DBC = \angle BAC$ .

Väite on yllä olevan perustelun nojalla uskottava, mutta tässä on väitteelle myös kunnollinen todistus.

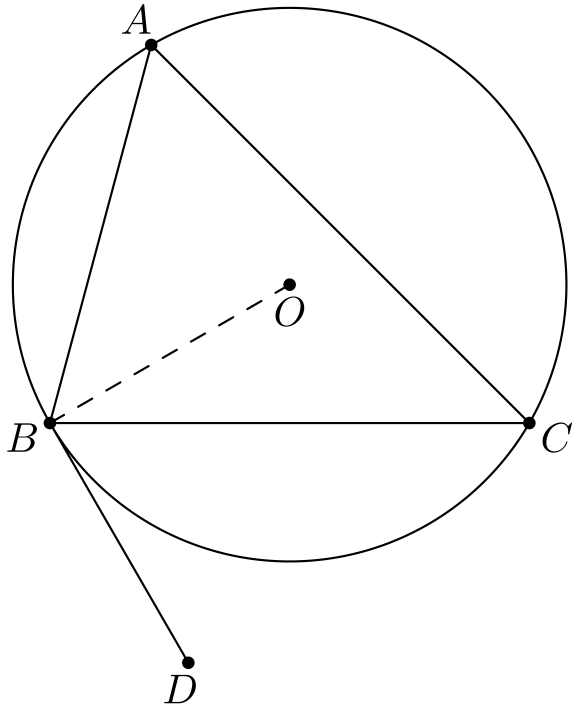
Kolmio ABC ympärysympyränsä sisällä. Ympyrän keskipiste O on merkitty, katkoviiva yhdistää sen kärkeen B, ja pisteen B kautta kulkeva tangenttisuora jatkuu pisteeseen D. — Kolmion $ABC$ ympärysympyrä ja tangentti $BD$ .

Kehäkulmalauseen nojalla $\angle BOC = 2\angle A$ , joten tasakylkisestä kolmiosta $BOC$ saadaan $\angle CBO = 90^{\circ} - \angle A$ . On tuttu juttu, että pisteeseen piirretty säde ja tangentti ovat kohtisuorassa toisiaan vastaan, eli $\angle DBO = 90^{\circ}$ . Täten $\angle DBC = \angle DBO - \angle CBO = 90^{\circ} - (90^{\circ} - \angle A) = \angle A.$

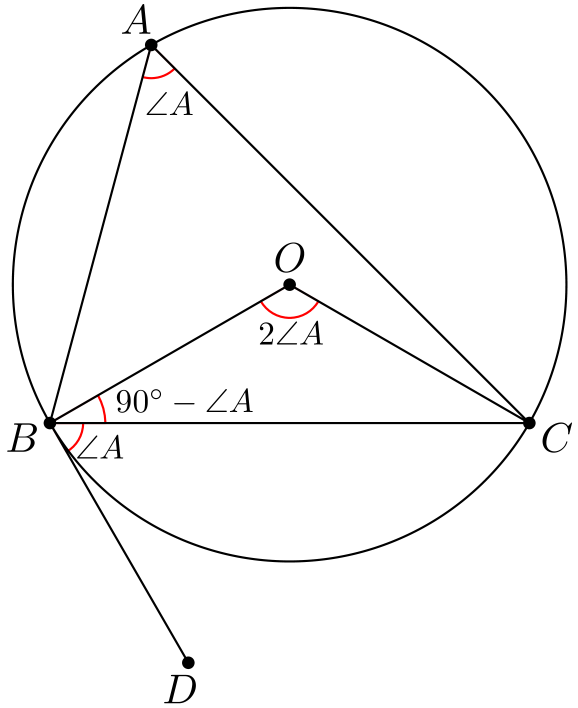
Sama kolmio ABC ympärysympyrineen kuin edellä, nyt kulmat merkittyinä. Kärjen A kulma on merkitty, keskuskulma pisteessä O on kaksi kertaa tämä kulma, kulma OBC on 90 astetta miinus kärjen A kulma, ja tangentin ja jänteen välinen kulma DBC on yhtä suuri kuin kärjen A kulma. — Kulmat merkittynä kuvioon.

Mainitaan vielä seuraava tulos:

Lause 14.2 (Kehäkulmalauseen tangenttiversion toinen suunta) Olkoon $ABC$ kolmio ja olkoon $D$ sellainen piste eri puolella suoraa $BC$ kuin piste $A$ , että $\angle DBC = \angle BAC$ . Tällöin $BD$ on tangentti kolmion $ABC$ ympärysympyrälle.

Väite seuraa yksikäsitteisyysargumentilla edellisestä tuloksesta samaan tapaan kuin kehäkulmalauseen toinen puoli saadaan kehäkulmalauseesta. Yksityiskohdat lyhyesti: Olkoon $D$ lauseen mukainen piste. Valitaan piste $D'$ tangentilta ja käytetään edellistä tulosta, jolloin saadaan $\angle DBC = \angle BAC = \angle D'BC.$ Täten $B, D$ ja $D'$ ovat samalla suoralla, eli $D$ on halutulla tangentilla.

14.3 Sisäympyrä

Tutkitaan kolmiota $ABC$ , sen sisäympyrää ja ympyrän sivuamispisteitä kolmion sivujen kanssa.

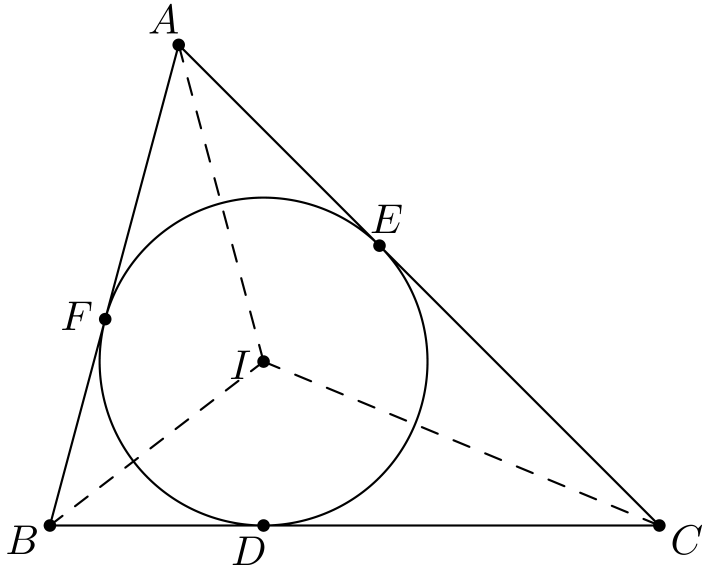
Kolmio ABC ja sen sisäympyrä, jonka keskipiste on I. Ympyrä sivuaa sivua BC pisteessä D, sivua AC pisteessä E ja sivua AB pisteessä F. Katkoviivat yhdistävät kärjet keskipisteeseen I. — Kuva 14.1: Kolmion sisäympyrä ja sivuamispisteitä.

Kuviosta löytyy jännenelikulmioita: $AFIE$ ja symmetrisesti $BDIF$ ja $CEID$ . Muutenkin kulmia osataan laskea kohtuullisen hyvin: pätee esimerkiksi $\angle BIC = 90^{\circ} + \angle A/2$ ja $\angle EDF = 90^{\circ} - \angle A/2$ . (Todistukset jätetään tehtäväksi 1.)

Tässä on pari hieman vaikeampaa huomiota.

Apulause 14.1 Jos $T$ on kolmion $ABC$ pinta-ala ja $r$ on sisäympyrän säde, niin $T = r \cdot \frac{AB + BC + CA}{2}.$

Todistuksen idea on hauska. Toisaalta kolmion $ABC$ pinta-ala on määritelmän nojalla $T$ . Toisaalta pinta-ala voidaan laskea kolmioiden $AIB, BIC$ ja $CIA$ pinta-alojen summana. Kolmion $AIB$ pinta-ala on kanta $AB$ kertaa korkeus $FI = r$ jaettuna kahdella eli $r \cdot AB/2$ . Samaan tapaan saadaan kahden muun pikkukolmion pinta-alat. Summaamalla saadaan lemman tulos.

Apulause 14.2 Pätee $AF = \frac{AB + AC - BC}{2}.$

Siis pituus $AF$ osataan laskea. Vastaavasti myös pituudet $FB, BD, DC, CE$ ja $EA$ osataan laskea.

Todistusta varten huomataan ensin, että $AF$ ja $AE$ ovat samasta pisteestä piirrettyjä tangentteja ympyrälle, joten ne ovat yhtä pitkiä.¹ Merkitään $x = AF$ , $y = BD$ ja $z = CE$ . Ideana on pystyttää yhtälöryhmä luvuille $x, y$ ja $z$ .

¹ Tarkka perustelu: Kulmat $\angle AFI$ ja $\angle AEI$ ovat suoria ja $IF = IE$ . Täten kolmiot $AFI$ ja $AEI$ ovat suorakulmaisia kolmioita, joiden yhdet kateetit ja hypotenuusat ovat yhtä pitkiä, joten myös toiset kateetit ovat yhtä pitkiä.

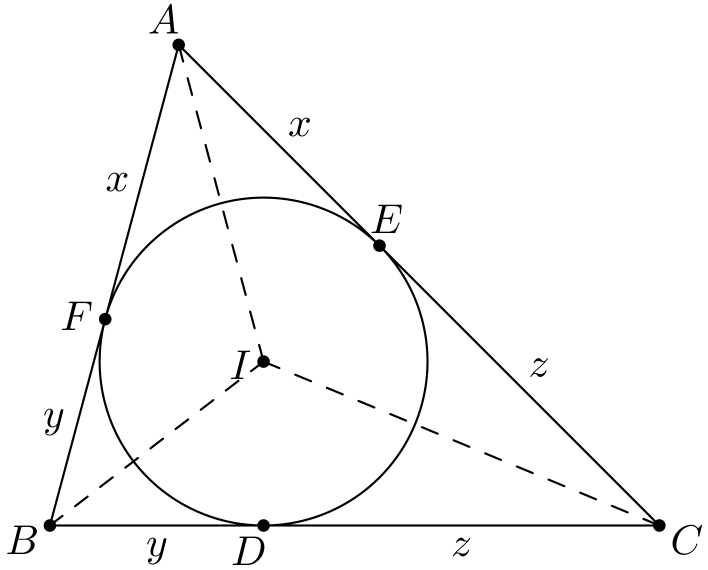
Edellinen sisäympyräkuvio, johon on lisätty sivuamispisteiden erottamien tangenttijanojen pituudet: kärjestä A lähtevät janat AF ja AE ovat molemmat pituudeltaan x, kärjestä B lähtevät BF ja BD ovat y, ja kärjestä C lähtevät CE ja CD ovat z. — Kuvio 14.1 täydennettynä tarvittavilla pituuksilla.

Tutkimalla kuviota luvuille $x, y$ ja $z$ saadaan yhtälöt $x + y = AB,$ $y + z = BC$ ja $z + x = AC.$ Loppu onkin algebrallista manipulaatiota. Summataan ensimmäinen ja kolmas yhtälö ja vähennetään tuloksesta keskimmäinen yhtälö. Saadaan $(x+y) + (z+x) - (y+z) = AB + AC - BC,$ mistä sieventämällä saadaan haluttu tulos.

14.4 Sivuympyrät

Palautetaan mieleen seuraava konfiguraatio yhdestä aiemmasta tehtävästä: jos $M$ on kolmion $ABC$ ympärysympyrän kaaren $BC$ keskipiste, niin $M$ on suoralla $AI$ ja $M$ on yhtä kaukana pisteistä $B, I$ ja $C$ (missä $I$ on kolmion sisäympyrän keskipiste).

Kolmio ABC ympärysympyrineen sekä sisäympyrän keskipiste I. Katkoviivainen ympyrä kulkee pisteiden B, I ja C kautta, ja sen keskipiste M on merkitty. — $M$ on kolmion $BIC$ ympärysympyrän keskipiste.

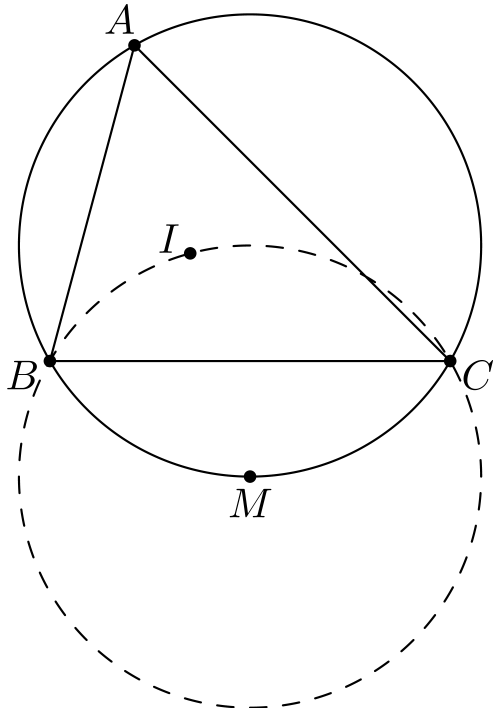
Jatketaan suoraa $AI$ pisteen $M$ yli kolmion $BIC$ ympärysympyrälle:

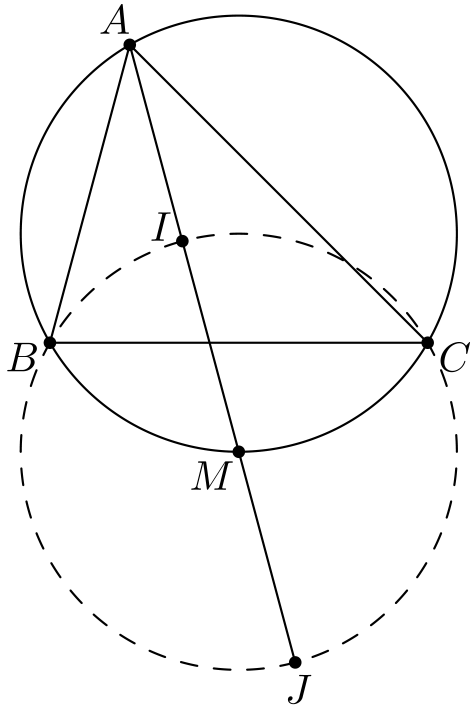
Sama kuvio kuin edellä, ja suora kärjestä A pisteiden I ja M kautta on jatkettu pisteeseen J katkoviivaympyrän kehälle, jolloin jana IJ on tämän ympyrän halkaisija. — Tutkitaan pistettä $J$ .

Nyt $IJ$ on ympyrän halkaisija, joten $IBJ$ on suora kulma. Koska $\angle CBI = \angle B / 2$ , niin $\angle JBC = 90^{\circ} - \angle B / 2$ . Tämä tarkoittaa, että $BJ$ on kulman $\angle ABC$ vieruskulman puolittaja: jos jatkamme janaa $AB$ pisteen $B$ yli johonkin pisteeseen $X$ , niin $BJ$ puolittaa kulman $\angle XBC$ .

Tästä seuraa, että $J$ on yhtä kaukana suorista $BC$ ja $BX$ . Vastaavasti $J$ on yhtä kaukana suorista $BC$ ja janan $AC$ jatkeesta. Voidaan siis piirtää $J$ -keskinen ympyrä, joka sivuaa näitä suoria. Tätä ympyrää kutsutaan kolmion $ABC$ (kärjen $A$ vastaiseksi) sivuympyräksi.

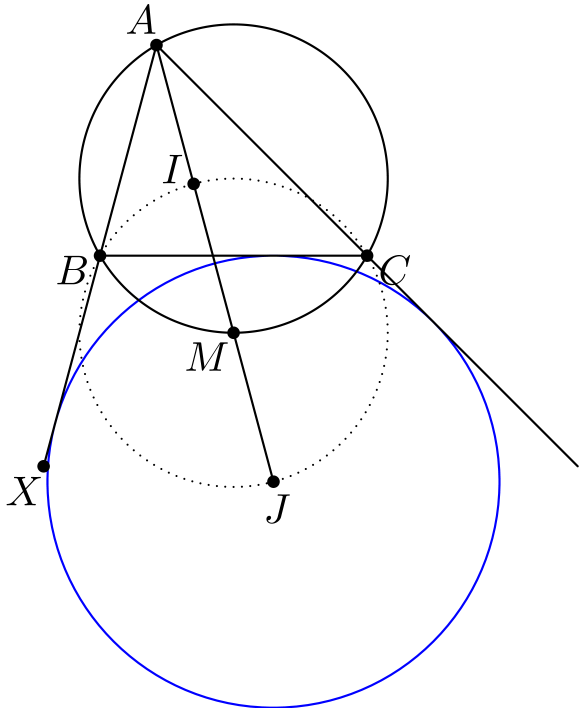
Sama kuvio täydennettynä sinisellä ympyrällä, jonka keskipiste on J. Tämä on kärjen A vastainen sivuympyrä: se sivuaa sivua BC sekä sivujen AB ja AC jatkeita, jotka on piirretty pisteiden B ja C ohi pisteisiin X ja Y. — Piste $J$ on kärjen $A$ vastaisen sivuympyrän keskipiste.

Kerätään tulokset seuraavaan lauseeseen.

Lause 14.3 (Sivuympyröiden peruslause) Olkoon $ABC$ kolmio, $I$ sen sisäympyrän keskipiste ja $M$ kolmion ympärysympyrän kaaren $BC$ keskipiste. Olkoon $J$ pisteen $I$ peilaus pisteen $M$ yli. Tällöin

$J$ on kolmion $ABC$ kärjen $A$ vastaisen sivuympyrän keskipiste
$BICJ$ on jännenelikulmio, jossa kulmat $\angle JBI$ ja $\angle ICJ$ ovat suoria
$BJ$ puolittaa kulman $\angle CBA$ vieruskulman.

14.5 Tehtäviä

Tehtävä 1. Osoita, että kuvan 14.1 tilanteessa $AFIE$ on jännenelikulmio, että $\angle BIC = 90^{\circ} + \angle A/2$ ja että $\angle EDF = 90^{\circ} - \angle A/2$ .

Tehtävä 2. Nelikulmiolla $ABCD$ on sisäympyrä (eli nelikulmion sisällä oleva ympyrä, joka sivuaa kaikkia nelikulmion sivuja). Osoita, että $AB + CD = BC + AD$ .

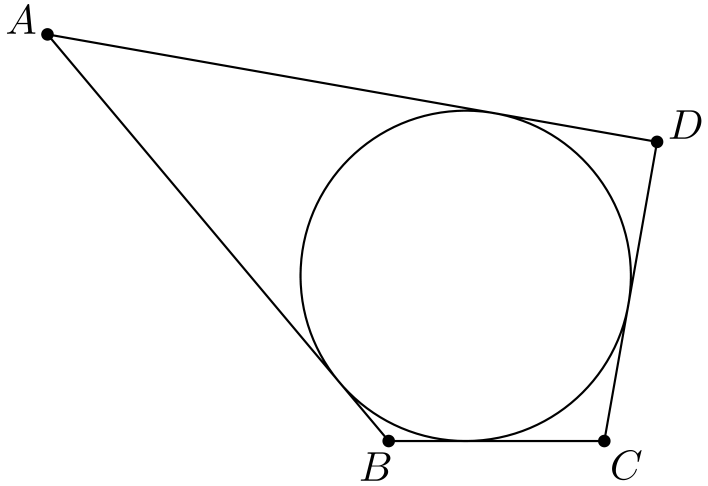
Ympyrä ja sen ympärille piirretty nelikulmio ABCD, jonka jokainen sivu sivuaa ympyrää. Kyseessä on tehtävän 2 sisäympyrällinen nelikulmio. — Tehtävä 2.

(Voidaan myös osoittaa, että jos konveksilla² nelikulmiolla $ABCD$ pätee $AB + CD = BC + AD$ , niin sillä on sisäympyrä.)

² Monikulmiota kutsutaan konveksiksi, jos sen kaikki kulmat ovat alle $180$ astetta.

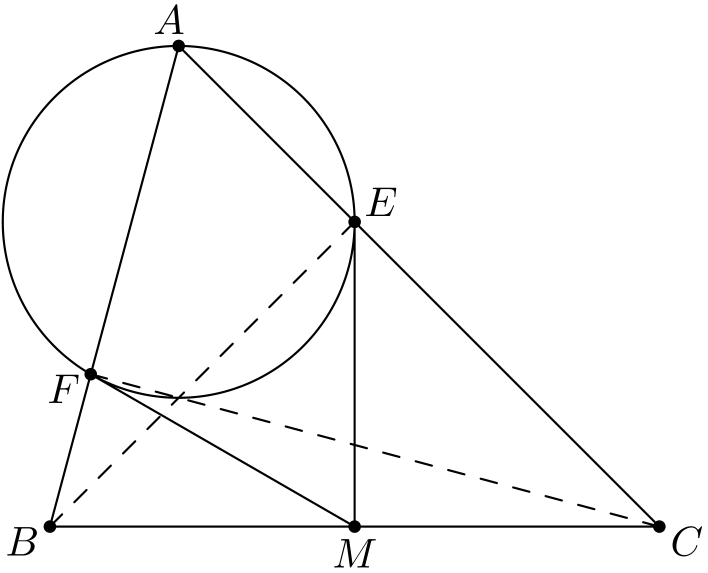
Tehtävä 3. Janat $BE$ ja $CF$ ovat kolmion $ABC$ korkeusjanoja. Piste $M$ on janan $BC$ keskipiste.

Osoita, että $MB = MF$ , $MF = ME$ ja $ME = MC$ .
Osoita, että janat $ME$ ja $MF$ ovat tangentteja kolmion $AEF$ ympärysympyrälle.

Kolmio ABC, jonka korkeusjanat BE ja CF on piirretty katkoviivoin ja osuvat sivuille pisteisiin E ja F. M on sivun BC keskipiste, ja siitä on piirretty janat pisteisiin E ja F. Kuvassa näkyy myös kolmion AEF ympärysympyrä. — Tehtävä 3.

Tehtävä 4. Olkoon $ABC$ kolmio, jonka korkeusjanat $AD, BE$ ja $CF$ leikkaavat pisteessä $H$ .

Olkoon $X$ janan $AH$ keskipiste. Osoita, että $DEXF$ on jännenelikulmio.
Olkoon $M$ janan $BC$ keskipiste. Osoita, että $DMEF$ on jännenelikulmio.

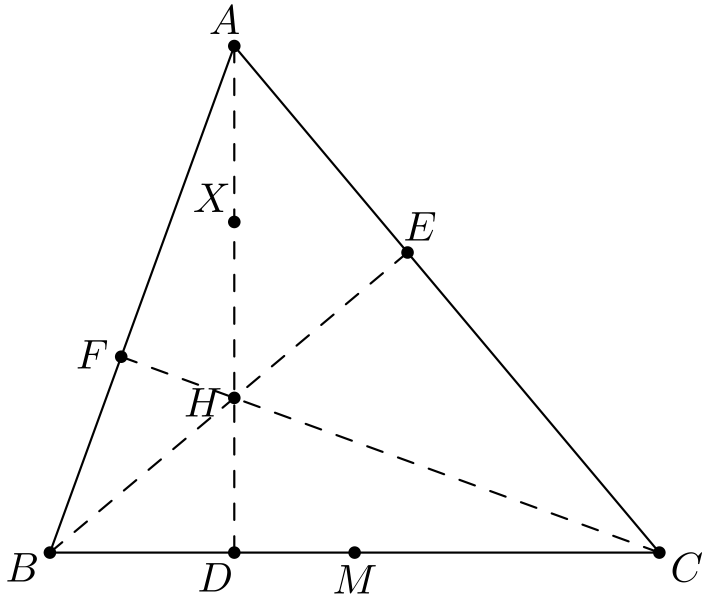
Kolmio ABC ja sen kolme korkeusjanaa katkoviivoin, jotka leikkaavat pisteessä H. Korkeusjanojen kannat sivuilla ovat D, E ja F. Lisäksi on merkitty janan AH keskipiste X ja sivun BC keskipiste M. — Tehtävä 4.

(Vastaavasti myös janojen $BH$ , $CH$ , $AC$ ja $AB$ keskipisteet ovat kolmion $DEF$ ympärysympyrällä. Tällä ympyrällä on siis peräti yhdeksän ”tärkeää” pistettä: $D, E$ ja $F$ , janojen $AH, BH$ ja $CH$ keskipisteet ja janojen $BC, AC$ ja $AB$ keskipisteet. Ympyrää kutsutaankin kolmion $ABC$ yhdeksän pisteen ympyräksi.)

Tehtävä 5. Kolmion $ABC$ ympärysympyrällä on piste $D$ . Pisteet $X, Y$ ja $Z$ ovat pisteestä $D$ suorille $BC, AC$ ja $AB$ piirrettyjen korkeusjanojen kannat. Osoita, että $X, Y$ ja $Z$ ovat samalla suoralla.

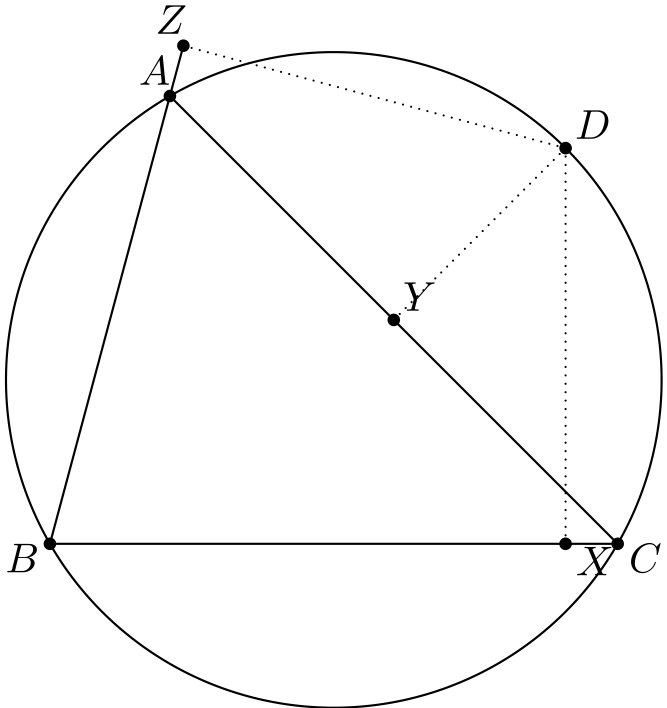
Kolmio ABC ympärysympyrineen ja ympyrän kehällä oleva piste D. Pisteestä D on piirretty pistekatkoviivoin kohtisuorat sivuille tai niiden jatkeille, ja kantapisteet X, Y ja Z ovat samalla suoralla. — Tehtävä 5.

(Suoraa kutsutaan Simsonin suoraksi.)

14.1 Johdanto

14.2 Kehä­kulma­lauseen tangentti­versio

14.3 Sisä­ympyrä

14.4 Sivu­ympyrät

14.5 Tehtäviä

14.2 Kehäkulmalauseen tangenttiversio

14.3 Sisäympyrä

14.4 Sivuympyrät