23  Epäyhtälöitä

Tekijä

Olli Järviniemi

23.1 Johdanto

Epäyhtälöitä tulee vastaan tietysti algebran tehtävissä, mutta myös kombinatoriikassa ja lukuteoriassa. Tässä tekstissä esitetään työkaluja, jotka sopivat niin puhtaisiin epäyhtälötehtäviin kuin sovelluskohteisiin.

23.2 QM-AM-GM-HM

Mietitään seuraavia kysymyksiä:

  1. Positiivisten lukujen \(a_1, a_2, \ldots , a_n\) summan tiedetään olevan \(s\). Kuinka pieni/suuri \(a_1^2 + a_2^2 + \ldots + a_n^2\) voi pienimmillään/suurimmillaan olla?
  2. Positiivisten lukujen \(a_1, a_2, \ldots , a_n\) summan tiedetään olevan \(s\). Kuinka pieni/suuri \(a_1a_2 \cdots a_n\) voi pienimmillään/suurimmillaan olla?
  3. Positiivisten lukujen \(a_1, a_2, \ldots , a_n\) summan tiedetään olevan \(s\). Kuinka pieni/suuri \(\frac{1}{a_1} + \frac{1}{a_2} + \ldots + \frac{1}{a_n}\) voi pienimmillään/suurimmillaan olla?

Tässä on vastaukset.

Kysymys (i): \(a_1^2 + \ldots + a_n^2\) on suurimmillaan, kun yksi luvuista on suunnilleen \(s\) ja muut luvut ovat suunnilleen \(0\), jolloin lausekkeen arvo on noin \(s^2\). Kertomalla auki nimittäin nähdään, että \[s^2 = (a_1 + a_2 + \ldots + a_n)^2 > a_1^2 + a_2^2 + \ldots + a_n^2.\] Pienimmillään neliöiden summa on silloin, kun kaikki luvuista ovat yhtä suuria (tämä perustellaan myöhemmin).

Kysymys (ii): Tulo voi olla niin lähellä nollaa kuin halutaan, koska jotkin luvuista \(a_i\) voidaan valita hyvin lähelle nollaa. Sen sijaan tulo on suurimmillaan silloin, kun kaikki luvuista ovat yhtä suuria (Arviointi ja epäyhtälöt -tekstissä nähtiin jonkinnäköinen perustelu, ja alla esitetään toinen). Siis tulo on enintään \((s/n)^n\).

Kysymys (iii): \(\frac{1}{a_1} + \ldots + \frac{1}{a_n}\) voidaan saada niin suureksi kuin halutaan valitsemalla jokin luvuista \(a_i\) olemaan hyvin pieni. Sen sijaan summan arvo on pienimmillään kun luvut \(a_i\) ovat yhtä suuria. Tällöin summan arvo on \(n^2/s\).

Seuraava lause kertoo vastauksen kunkin kysymyksen vaikeampaan puoleen.

Lause 23.1 (QM-AM-GM-HM) Olkoot \(a_1, \ldots , a_n\) positiivisia lukuja. Tällöin pätee \[\begin{eqnarray} \sqrt{\frac{a_1^2 + a_2^2 + \ldots + a_n^2}{n}} &\ge& \frac{a_1 + a_2 + \ldots + a_n}{n} \\ &\ge& \sqrt[n]{a_1a_2 \cdots a_n} \\ &\ge& \frac{n}{\frac{1}{a_1} + \frac{1}{a_2} + \ldots + \frac{1}{a_n}}.\end{eqnarray}\] Jos jossakin epäyhtälössä pätee yhtäsuuruus, niin \(a_1 = a_2 = \ldots = a_n\).

Vasemmalta oikealle tehtävän lausekkeita kutsutaan lukujen \(a_1, \ldots , a_n\) kvadraattiseksi keskiarvoksi, aritmeettiseksi keskiarvoksi, geometriseksi keskiarvoksi ja harmoniseksi keskiarvoksi. Tästä tulee lauseen nimitys QM-AM-GM-HM (esim. kvadraattinen keskiarvo on englanniksi ”quadratic mean”).1

  • 1 Keskiarvoille löytyy ”oikean elämän” tulkintoja. Aritmeettinen keskiarvo on tavallinen keskiarvo. Geometrinen keskiarvo voidaan tulkita niin, että jos maan väkiluku ensimmäisenä vuonna \(a_1\)-kertaistuu, toisena \(a_2\)-kertaisuu ja niin edelleen \(n\) vuoden ajan, kasvaa väkiluku saman verra kuin jos se olisi joka vuosi \(\sqrt[n]{a_1 \cdots a_n}\)-kertaistunut. Harmoninen keskiarvo: jos auto ajaa yhden kilometrin nopeudella \(a_1\) kilometriä tunnissa, toisen nopeudella \(a_2\) kilometriä tunnissa ja niin edelleen, on keskinopeus \(n/(1/a_1 + \ldots + 1/a_n)\) kilometriä tunnissa.

    • Todistetaan tässä QM-AM- ja AM-HM-epäyhtälöt. Geometriseen keskiarvoon palataan tämän tekstin loppupuolella.

    Alla on epäyhtälöiden todistukset. Todistusten idea on tärkeä: kohtalaisen vaikeitakin tuloksia saa todistettua ryhmittelemällä vain termejä sopivasti neliöiden summiksi. Esimerkiksi ainoa varsinainen epäyhtälö, jota alla olevat todistukset käyttävät, on \((a-b)^2 \ge 0\), josta saadaan \(a^2 + b^2 \ge 2ab\).

    QM-AM. Riittää todistaa neliöity epäyhtälö \[\frac{a_1^2 + \ldots + a_n^2}{n} \ge \frac{(a_1 + \ldots + a_n)^2}{n^2}.\] Kerrotaan oikean puolen tulo auki. Tästä saadaan summa \[\sum_{\substack{1 \le i \le n \\ 1 \le j \le n}} a_ia_j,\] missä \(i\) ja \(j\) käyvät yhteensä \(n^2\) eri termiä läpi. Käytetään tähän epäyhtälöä \(a_ia_j \le \frac{1}{2}(a_i^2 + a_j^2)\). Saadaan \[\begin{align*} \frac{(a_1 + \ldots + a_n)^2}{n^2} &= \frac{1}{n^2} \sum_{\substack{1 \le i \le n \\ 1 \le j \le n}} a_ia_j \\ &\le \frac{1}{n^2} \sum_{\substack{1 \le i \le n \\ 1 \le j \le n}} \frac{1}{2}(a_i^2 + a_j^2) \\ &= \frac{1}{n^2} \sum_{1 \le k \le n} na_k^2 \\ &= \frac{a_1^2 + \ldots + a_n^2}{n}, \end{align*}\] mikä on haluttu epäyhtälö.

    AM-HM. Kerrotaan epäyhtälöä auki. Riittää todistaa \[(a_1 + a_2 + \ldots + a_n)\left(\frac{1}{a_1} + \ldots + \frac{1}{a_n}\right) \ge n^2.\] Kerrotaan taas tulo auki. Ulos tulee ensinnäkin termejä muotoa \(\frac{a_i}{a_i}\), jokaiselle \(1 \le i \le n\) yksi kappale. Näiden termien summa on \(n\).

    Lisäksi ulos tulee \(n^2 - n\) kappaletta termejä muotoa \(\frac{a_i}{a_j}\), missä \(i \neq j\). Nämä voidaan ryhmitellä pareihin \(\frac{a_i}{a_j} + \frac{a_j}{a_i}\). Tämä summa on vähintään kaksi, koska \[\frac{a_i}{a_j} + \frac{a_j}{a_i} = \frac{a_i^2 + a_j^2}{a_ia_j} \ge \frac{2a_ia_j}{a_ia_j} = 2.\] Täten näiden \((n^2 - n)/2\) parin summa on vähintään \(n^2 - n\).

    Kaiken kaikkiaan auki kerrottu summa on siis vähintään \(n^2\).

    23.3 Jensenin epäyhtälö

    Lämmittelykysymys: Kumpi luvuista \(\sqrt{6} + \sqrt{8}\) ja \(2\sqrt{7}\) on suurempi?

    Vastaus: \(2\sqrt{7}\). Epäyhtälön \(\sqrt{6} + \sqrt{8} < 2\sqrt{7}\) voi kirjoittaa muotoon \[\sqrt{8} - \sqrt{7} < \sqrt{7} - \sqrt{6}.\] Epäyhtälö pätee, koska neliöjuuren kasvunopeus hidastuu lukujen kasvaessa, ja siten \(\sqrt{8}\) ja \(\sqrt{7}\) ovat lähempänä toisiaan kuin \(\sqrt{7}\) ja \(\sqrt{6}\).

    Jensenin epäyhtälö yleistää tätä ideaa. Ennen epäyhtälön esittämistä pitää selittää, mitä tarkalleen tarkoittaa, että funktion ”kasvunopeus hidastuu” (tai vastaavasti että kasvunopeus kasvaa). Tämän ominaisuuden omaavaa funktiota kutsutaan konkaaviksi (vastaavasti konveksiksi).

    23.3.1 Konveksisuus ja konkaavius

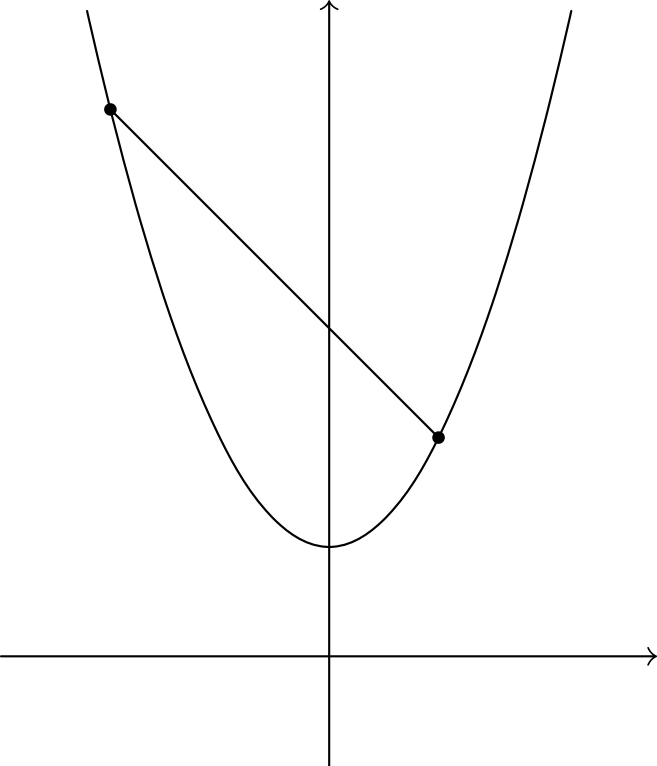
    Määritelmä 23.1 Funktio \(f\) on konveksi, jos valittaessa mitkä tahansa kaksi kuvaajan pistettä on pisteiden välinen jana kuvaajan yläpuolella (tai sen päällä).

    Mikä tahansa kuvaajan pisteiden välinen jana kulkee kuvaajan yläpuolella.

    Tämän geometrisen ehdon voi esittää myös algebrallisesti. Valitaan jokin piste \(C\) pisteiden väliseltä janalta. Se saadaan ottamalla painotettu keskiarvo pisteistä: painotetaan pistettä \((a, f(a))\) painolla \(t\) ja pistettä \((b, f(b))\) painolla \(1-t\), missä \(0 \le t \le 1\). Nyt pisteen \(C\) \(x\)-koordinaatti on \(ta + (1-t)b\) ja \(y\)-koordinaatti on \[tf(a) + (1-t)f(b).\]

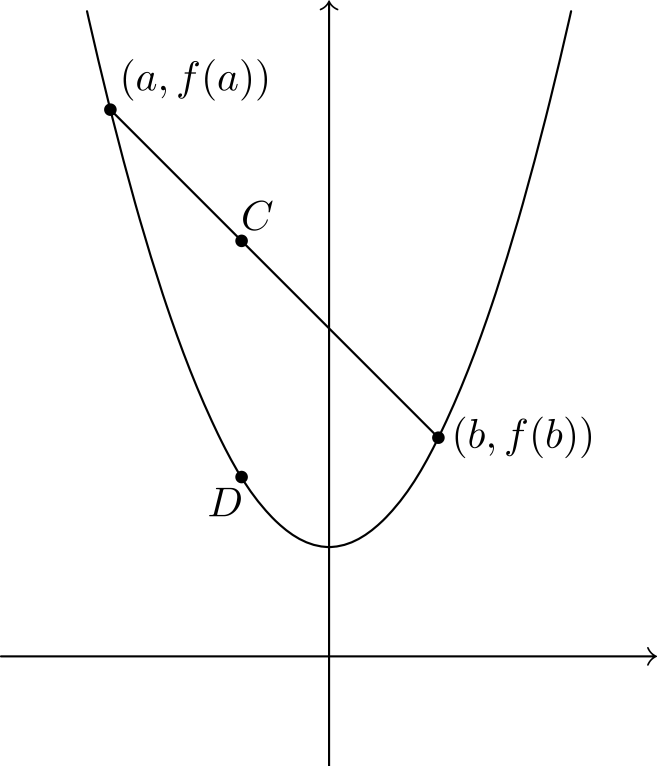
    Janalta valittu piste \(C\) on kuvaajan pisteen \(D\) yläpuolella.

    Valitaan sitten kuvaajalta vastaavasta kohdasta piste \(D\), eli valitaan kuvaajan piste, jonka \(x\)-koordinaatti on \(ta + (1-t)b\). Sen \(y\)-koordinaatti on \(f(ta + (1-t)b)\). Täten funktio \(f\) on konveksi täsmälleen silloin, kun \[tf(a) + (1-t)f(b) \ge f(ta + (1-t)b) \qquad \text{ kaikilla } 0 \le t \le 1.\]

    Konveksisuus tarkoittaa, että funktion kasvunopeus kasvaa. Vastaavasti voidaan määritellä konkaavi funktio olemaan sellainen, jolla kahden funktion kuvaajan pisteen välinen jana on kuvaajan alapuolella. Samanlaisella päättelyllä kuin yllä saadaan, että funktio on konkaavi jos \(tf(a) + (1-t)f(b) \le f(ta + (1-t)b)\) kaikilla \(0 \le t \le 1\).

    Käytännössä helpoin tapa tutkia kasvaako funktion kasvunopeus on tutkimalla sen derivaattoja2. Funktio \(f\) on konveksi täsmälleen silloin, kun \(f''(x) \ge 0\) kaikilla \(x\) (olettaen, että funktiota \(f\) todella voidaan derivoida kaksi kertaa) ja konkaavi jos \(f''(x) \le 0\).

  • 2 …jos on jo lukiossa opiskellut derivaatat. Muussa tapauksessa: sivuuta toistaiseksi kohdat, joita et ymmärrä.

    • Tässä on listattu muutamia tärkeitä konvekseja ja konkaaveja funktioita.

    • \(f(x) = x^n\) on konveksi positiivisilla luvuilla \(x\), kun \(n \ge 1\).
    • \(f(x) = \sqrt{x}\) on konkaavi.
    • \(f(x) = e^x\) on konveksi.
    • \(f(x) = \ln(x)\) on konkaavi.
    • \(f(x) = \frac{1}{x}, x > 0\) on konveksi.

    Eli monien tuttujen funktioiden tapauksessa funktion kuvaajan perusteella tehty arvaus konveksisuudesta/konkaaviudesta on oikein.

    23.3.2 Jensenin epäyhtälö

    Tässä on tämän aliluvun päätulos. Epäyhtälölle esitetään sovelluksia seuraavassa aliluvussa.

    Lause 23.2 (Jensenin epäyhtälö) Olkoon \(f(x)\) konveksi funktio ja olkoot \(x_1, x_2, \ldots , x_n\) lukuja. Tällöin \[\frac{f(x_1) + f(x_2) + \ldots + f(x_n)}{n} \ge f\left(\frac{x_1 + x_2 + \ldots + x_n}{n}\right).\] Jos \(f\) on konkaavi funktio, epäyhtälö pätee toiseen suuntaan.

    Annetaan lauseelle tiivis todistus. Todistuksen idea on todistaa yleisempi väite induktiolla. (Käsittelemme vain tapauksen, jossa \(f\) on konveksi, koska konkaavi tapaus on samankaltainen.)

    Todistus. Todistetaan yleisemmin, että jos \(t_1, t_2, \ldots , t_n\) ovat painokertoimia, jotka ovat vähintään nolla ja joiden summa on \(1\), niin \[t_1f(x_1) + t_2f(x_2) + \ldots + t_nf(x_n) \ge f(t_1x_1 + \ldots + t_nx_n).\] Jensenin epäyhtälö saadaan valitsemalla painokertoimet olemaan \(t_1 = t_2 = \ldots = t_n = 1/n\).

    Tapaus \(n = 2\) on konveksisuuden määritelmä. Suoritetaan induktioaskel.

    Olkoot \(t_1, \ldots , t_{n+1}\) ja \(x_1, \ldots , x_{n+1}\) annettuja lukuja. Pakotetaan summa \(t_1f(x_1) + \ldots + t_{n}f(x_{n})\) muotoon, johon voidaan käyttää induktio-oletusta (eli yritetään saada painokertoimien summaksi \(1\)) ja käytetään sitten induktio-oletusta:

    \[\begin{eqnarray} & & t_1f(x_1) + t_2f(x_2) + \ldots + t_nf(x_n) + t_{n+1}f(x_{n+1}) \\ &=& (t_1 + \ldots + t_n)\left(\frac{t_1}{t_1 + \ldots + t_n}f(x_1) + \ldots + \frac{t_n}{t_1 + \ldots + t_n}f(x_n)\right) + t_{n+1}f(x_{n+1}) \\ &\ge& (t_1 + \ldots + t_n)f\left(\frac{t_1x_1 + t_2x_2 + \ldots + t_nx_n}{t_1 + \ldots + t_n}\right) + t_{n+1}f(x_{n+1}). \end{eqnarray}\]

    Väite seuraa soveltamalla tähän konveksisuuden määritelmää.

    23.3.3 Sovelluksia

    QM-AM: Funktio \(f(x) = x^2\) on konveksi, joten jos \(a_1, \ldots , a_n\) ovat joitakin lukuja, niin \[\frac{a_1^2 + a_2^2 + \ldots + a_n^2}{n} \ge \left(\frac{a_1 + a_2 + \ldots + a_n}{n}\right)^2.\] Ottamalla tästä neliöjuuri saadaan QM-AM-epäyhtälö.

    AM-GM: Funktio \(f(x) = e^x\) on konveksi, joten jos \(b_1, \ldots , b_n\) ovat joitakin lukuja, niin \[\frac{e^{b_1} + e^{b_2} + \ldots + e^{b_n}}{n} \ge e^{\frac{b_1 + b_2 + \ldots + b_n}{n}} = \sqrt[n]{e^{b_1} \cdot e^{b_2} \cdot \ldots \cdot e^{b_n}}.\] Nyt jos \(a_1, \ldots , a_n\) ovat positiivisia lukuja, niin valitaan yllä olevassa epäyhtälössä \(b_i = \ln(a_i)\), jolloin saadaan AM-GM-epäyhtälö.

    GM-HM: Kuten AM-GM -epäyhtälön todistuksessa, \[\frac{e^{b_1} + e^{b_2} + \ldots + e^{b_n}}{n} \ge \sqrt[n]{e^{b_1} \cdot e^{b_2} \cdot \ldots \cdot e^{b_n}}.\] Valitaan luvut \(b_i\) niin, että \(e^{b_i} = 1/a_i\). Ristiin kertomisten ja jakamisten jälkeen saadaan \[\sqrt[n]{a_1 \cdots a_n} \ge \frac{n}{\frac{1}{a_1} + \cdots + \frac{1}{a_n}},\] mikä on haluttu väite.

    23.4 Lisäesimerkki

    Esitetään vielä esimerkki, joka ei liity Jensenin epäyhtälöön.

    Tehtävä 23.1 Positiivisten lukujen \(a, b\) ja \(c\) summa on \(1\). Kuinka suuri \(a^3b^2c\) voi olla enimmillään?

    Tilanne muistuttaa hieman aritmeettis-geometrista epäyhtälöä, joka antaa \[\frac{1}{3} \ge \frac{a+b+c}{3} \ge \sqrt[3]{abc}\] Oikealla kuitenkin esiintyy termi \(abc\) eikä haluamamme \(a^3b^2c\).

    Miten saamme oikealle termin \(a^3b^2c\)? Voisimme yrittää soveltaa AM-GM:ää seuraavasti: \[\frac{a + a + a + b + b + c}{6} \ge \sqrt[6]{a^3b^2c}.\] Tässäkin on ongelmansa: vasemmalle puolelle tulee lauseke \(3a + 2b + c\), jota ei osata arvioida.

    Ideana on käyttää AM-GM:ää luvuille, jotka eivät ole \(a, b\) ja \(c\) vaan painotettuja versioita niistä. Pätee \[\frac{a/3 + a/3 + a/3 + b/2 + b/2 + c}{6} \ge \sqrt[6]{(a/3)^3(b/2)^2c}.\] (Ei ihan helppo keksiä itse.) Epäyhtälön vasen puoli on \(1/6\), joten saamme \[(a/3)^3(b/2)^2c \le 1/6^6,\] eli laskujen jälkeen \[a^3b^2c \le \frac{1}{432}.\]

    AM-GM:ssä pätee yhtäsuuruus, kun luvut ovat yhtä suuria, eli kun \(a/3 = b/2 = c\). Yhdistettynä tietoon \(a+b+c = 1\) tämä tarkoittaa, että \(a^3b^2c\) saa maksimiarvonsa, kun \(a = 1/2, b = 1/3\) ja \(c = 1/6\), jolloin tosiaan pätee \(a^3b^2c = 1/432\).

    Kommentti. Miten voi päätyä painottamaan AM-GM:ää esitetyllä tavalla?

    Yksi tapa on miettiä, miten AM-GM-epäyhtälön vasemmalle ja oikealle puolelle saadaan sopivanlaiset lausekkeet (\(a+b+c\) ja \(a^3b^2c\)).

    Toinen tapa on miettiä tarkkaan epäyhtälön yhtäsuuruustapauksia. On selvää, että \(a^3b^2c\) ei ole suurimmillaan, kun \(a = b = c\): on järkevää panostaa siihen, että \(a\) on suuri, koska lukua \(a\) on tulossa \(a^3b^2c\) kolme kappaletta. Sen sijaan jos AM-GM:ää sovelletaan vaikkapa muodossa \[\frac{a + a + a + b + b + c}{6} \ge \sqrt[6]{a^3b^2c},\] pätee yhtäsuuruus kun \(a = b = c\). Yhtäsuuruustapaukset menevät väärin, joten lähestymistapa ei voi toimia.

    Siis aritmeettis-geometrisen epäyhtälön soveltamisessa pitää ottaa huomioon se, milloin \(a^3b^2c\) saa maksimiarvonsa. Tämä onnistuu painottamalla lukuja sopivasti.

    23.5 Tehtäviä

    Tehtävä 1. Osoita, että jos \(a, b\) ja \(c\) ovat positiivisia lukuja, niin \[\frac{a}{b} + \frac{b}{c} + \frac{c}{a} \ge 3.\]

    Tehtävä 2. Osoita, että jos \(a, b\) ja \(c\) ovat positiivisia lukuja, niin \[(a+b)(b+c)(c+a) \ge 8abc.\]

    Tehtävä 3. Polynomin \(x^3 - ax^2 + bx - 1\) kaikki kolme nollakohtaa ovat positiivisia. Osoita, että \(a \ge 3\) ja \(b \ge 3\).

    Tehtävä 4. Osoita, että jos \(a, b, c\) ja \(d\) ovat positiivisia lukuja, niin \[\frac{1}{a} + \frac{1}{b} + \frac{4}{c} + \frac{16}{d} \ge \frac{64}{a+b+c+d}.\]

    Tehtävä 5. Osoita, että jos \(a, b\) ja \(c\) ovat positiivisia lukuja, niin \[a^3 + b^3 + c^3 \ge a^2b + b^2c + c^2a \ge 3abc.\]

    Tehtävä 6. Tunnettu Cauchyn-Schwarzin epäyhtälö sanoo, että jos \(a_1, a_2, \ldots , a_n\) ja \(b_1, b_2, \ldots , b_n\) ovat reaalilukuja, niin \[\left(\sum_{i = 1}^n a_ib_i\right)^2 \le \left(\sum_{i = 1}^n a_i^2\right)\left(\sum_{i = 1}^n b_i^2\right).\]

    1. Todista QM-AM-HM-epäyhtälöt Cauchyn-Schwarzin epäyhtälöllä valitsemalla luvut \(b_1, \ldots , b_n\) sopivasti
    2. Todista Cauchyn-Schwarzin epäyhtälö.