6 Jännenelikulmiot

Tekijä

Olli Järviniemi

6.1 Johdanto

Edellisessä tekstissä käsiteltiin kehäkulmalausetta: jos ympyrän kehältä valitaan pisteitä, niin tietyt kulmat ovat yhtä suuria. Tässä tekstissä käsitellään tuloksia, jotka menevät toiseen suuntaan: jos tietyt neljän pisteen väliset kulmat ovat yhtä suuria, niin pisteet ovat samalla ympyrällä.

6.2 Kehäkulmalauseen toinen suunta

Seuraavassa kuvassa on pisteet \(A, B, X\) ja \(Y\). Tiedetään, että kulmat \(\angle AXB\) ja \(\angle AYB\) ovat yhtä suuria.

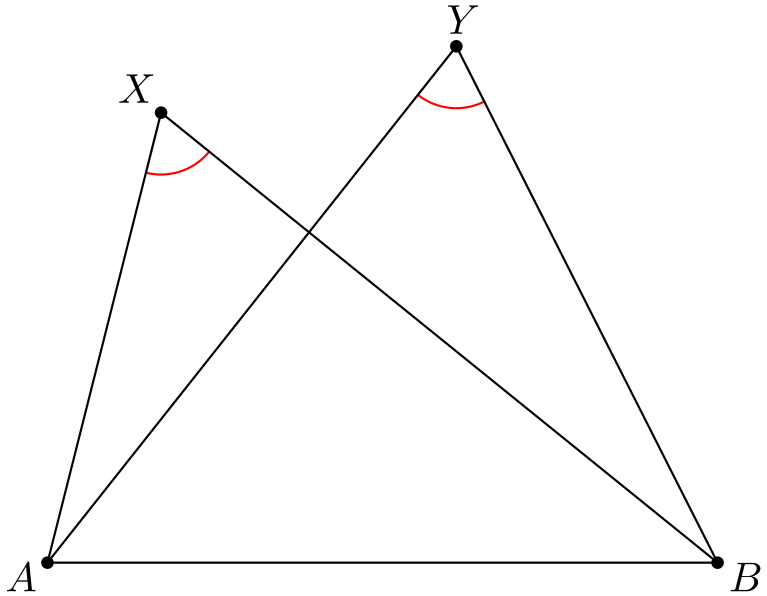
Kuva 1: Kehäkulmalausetta muistuttava kuvio.

Tilanne muistuttaa vahvasti kehäkulmalausetta, jossa saatiin vastaavanlainen kulmaehto siinä tilanteessa, että pisteet ovat saman ympyrän kehällä. On siis luontevaa kysyä: ovatko yllä olevan kuvan pisteet välttämättä saman ympyrän kehällä?

Vastaus on myönteinen. Tämä on tämän luvun pääaihe.

Lause 6.1 (Kehäkulmalauseen toinen suunta) Olkoot \(A, B, X\) ja \(Y\) pisteitä. Oletetaan, että \(X\) ja \(Y\) ovat samalla puolella janaa \(A\) ja \(B\) ja että \(\angle AXB = \angle AYB\). Tällöin pisteet \(A, B, X\) ja \(Y\) ovat saman ympyrän kehällä.

Tulos on kätevä: Jos tiedämme yhden kulmaehdon (\(\angle AXB = \angle AYB\)), seuraa tästä, että pisteet ovat samalla ympyrällä. Tällöin pääsemme käyttämään kehäkulmalausetta, ja saamme paljon lisää kulmaehtoja (esimerkiksi \(\angle XBA = \angle XYA\) ja \(\angle BAX + \angle XYB = 180^{\circ}\)). Saamme siis monta kulmaehtoa yhden hinnalla!

Lauseen todistusta varten tarvitsemme hieman valmistelua.

6.3 Ympyrä kolmen pisteen kautta

Ennen kuin mietitään, milloin neljän pisteen kautta voidaan piirtää ympyrä, on luontevaa miettiä kolmen pisteen tapausta. Milloin kolmen pisteen kautta voidaan piirtää ympyrä?

Vastaus: aina, kunhan pisteet eivät ole samalla suoralla.

Lause 6.2 (Kolmion ympärysympyrä) Jos \(A, B\) ja \(C\) ovat pisteitä, jotka eivät ole samalla suoralla, niin on olemassa tasan yksi ympyrä, joka kulkee kunkin pisteen \(A, B\) ja \(C\) kautta.

Kolme pistettä määräävät siis yksikäsitteisen ympyrän. Neljällä pisteellä väite ei enää päde: on poikkeuksellista, että neljä pistettä sattuvat olemaan samalla ympyrällä. Tämä tekee kehäkulmalauseen toisesta suunnasta mielenkiintoisen.

Lähdetään todistamaan väitettä. Tutkitaan siis joitakin kolmea pistettä.

Kuva 2: Kolme pistettä, jotka eivät ole samalla suoralla.

Mihin ympyrän keskipiste tulee laittaa? Keskipisteen tulee olla sellaisessa kohdassa, jossa se on yhtä kaukana kustakin annetusta pisteestä. Ei ole selvää, miksi tällainen kohta on olemassa tai missä se on.

Tutkitaan helpompaa tapausta eli kahta pistettä. Missä ovat ne pisteet, jotka ovat yhtä kaukana pisteistä \(B\) ja \(C\)? Ainakin janan \(BC\) keskipiste on tällainen piste. Miettimällä hieman huomataan, että sopivat pisteet sijaitsevat janan \(BC\) keskinormaalilla¹ ja että kaikki janan \(BC\) keskinormaalilla olevat pisteet ovat yhtä kaukana pisteistä \(B\) ja \(C\):

¹ Janan (tai suoran) normaali on sellainen suora, joka on sitä vastaan kohtisuorassa. Janan keskinormaali on se normaali, joka jakaa janan kahteen yhtä pitkään osaan.

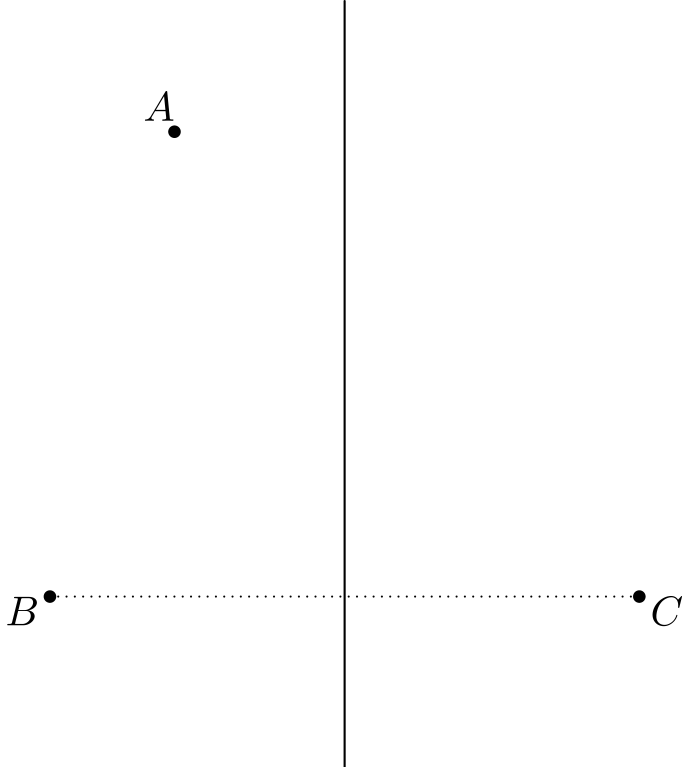
Kuva 3: Ne pisteet, jotka ovat yhtä kaukana pisteistä \(B\) ja \(C\), muodostavat suoran.

Entä missä ovat ne pisteet, jotka ovat yhtä kaukana pisteistä \(A\) ja \(B\)? Nämä ovat vastaavasti janan \(AB\) keskinormaalin pisteet:

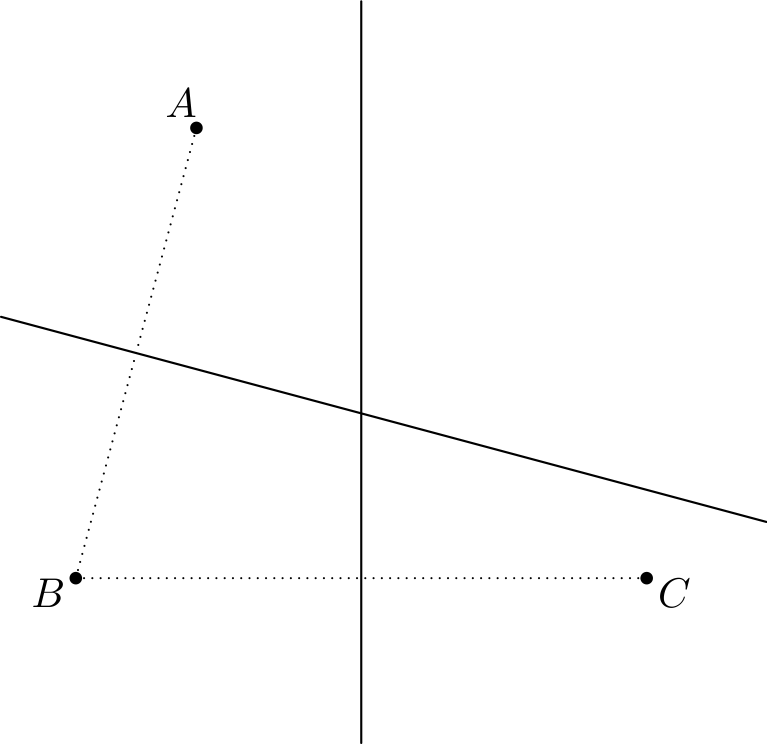
Kuva 4: Janojen \(AB\) ja \(BC\) keskinormaalit leikkaavat.

Nämä keskinormaalit leikkaavat jossakin pisteessä.² Tämä piste kelpaa: Leikkauspiste on \(BC\):n keskinormaalilla, joten se on yhtä kaukana pisteistä \(B\) ja \(C\), ja koska se on \(AB\):n keskinormaalilla, se on yhtä kaukana pisteistä \(A\) ja \(B\). Täten se on yhtä kaukana kaikista pisteistä \(A, B\) ja \(C\). Voimme siis piirtää ympyrän, jonka keskipiste on tämä leikkauspiste ja joka kulkee pisteiden \(A, B\) ja \(C\) kautta.

² Tässä tarvitaan tietoa siitä, etteivät \(A, B\) ja \(C\) ole samalla suoralla. Jos pisteet ovat samalla suoralla, niin keskinormaalit ovat yhdensuuntaisia eivätkä leikkaa.

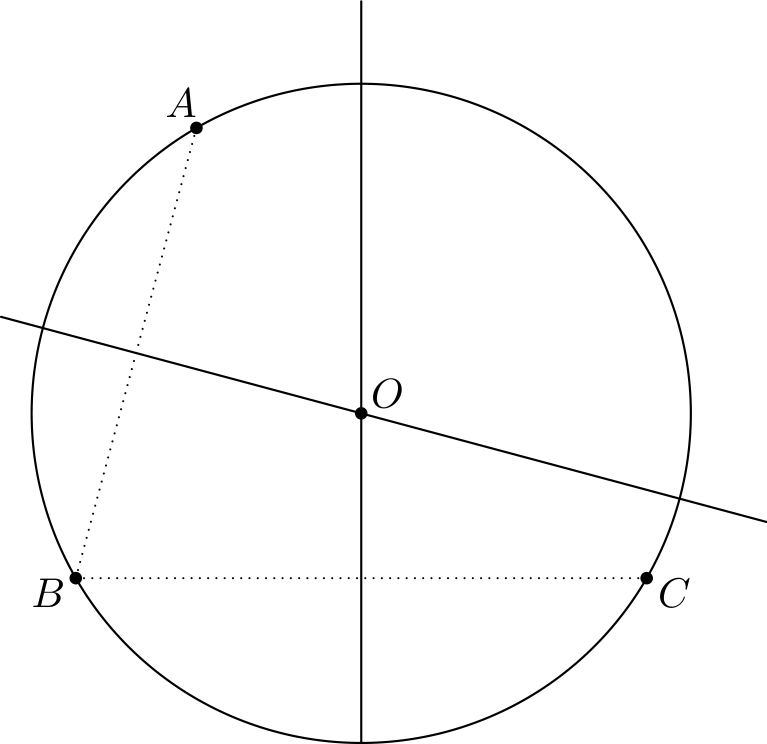
Kuva 5: Keskinormaalien leikkauspiste \(O\) kelpaa ympyrän keskipisteeksi.

Perustelusta nähdään myös, ettei tällaisia ympyröitä ole useampia.

Ympyrää kutsutaan kolmion \(ABC\) ympärysympyräksi tai ympäri piirretyksi ympyräksi.

6.4 Kehäkulmalauseen toisen suunnan todistus

Tutkitaan jälleen seuraavan kuvan tilannetta. Haluamme osoittaa, että \(A, B, X\) ja \(Y\) ovat samalla ympyrällä.

Kuva 6: Osoitetaan, että kuvan pisteet ovat jonkin ympyrän kehällä.

Piirretään ympyrä pisteiden \(A, B\) ja \(X\) kautta. Edellisen osion päättelyn nojalla tiedämme, että tämä on mahdollista. Yritetään perustella, että myös \(Y\) on tällä ympyrällä.

Miltä tilanne näyttäisi, jos \(Y\) ei olisi tällä ympyrällä? Jos \(Y\) on ympyrän ulkopuolella, näyttää tilanne tältä:

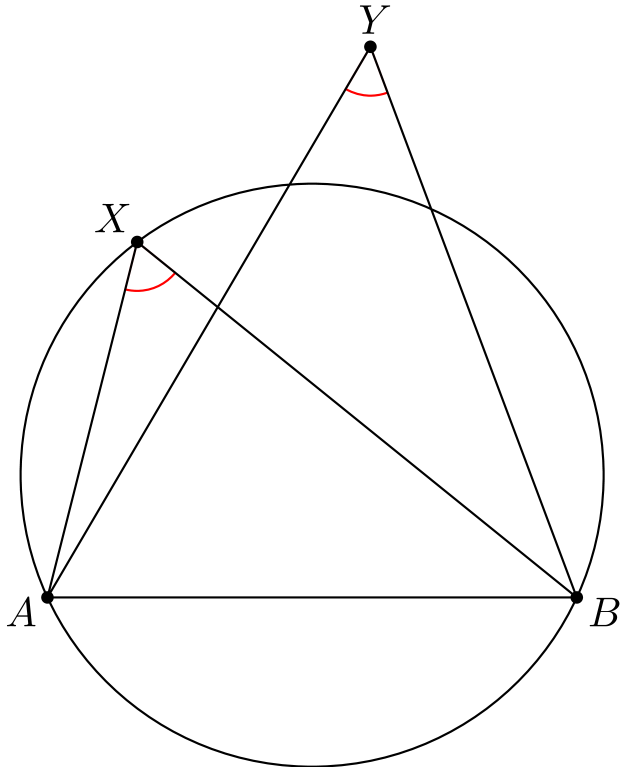
Kuva 7: Kuvitteellinen tilanne, jossa \(Y\) on ympyrän ulkopuolella.

Piirretään kuvaan janan \(BY\) leikkauspiste ympyrän kanssa. Olkoon tämä leikkauspiste \(Y'\).

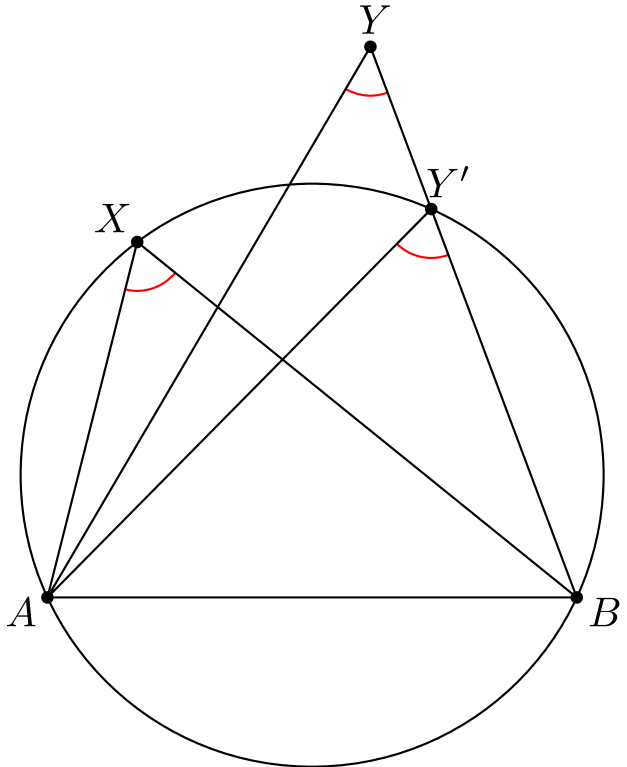
Kuva 8: Tutkitaan janan \(BY\) leikkauspistettä ympyrän kanssa.

Huomataan, että kehäkulmalauseen nojalla \(\angle AY'B = \angle AXB\), joka puolestaan on sama kuin kulma \(\angle AYB\). Nyt kolmiossa \(AYY'\) kulmien \(\angle AYY'\) ja \(\angle YY'A\) summa on \(180^{\circ}\), eli kolmas kulma \(\angle Y'AY\) on nolla astetta. Tämä tilanne on mahdoton, joten \(Y\) ei voi olla ympyrän ulkopuolella.

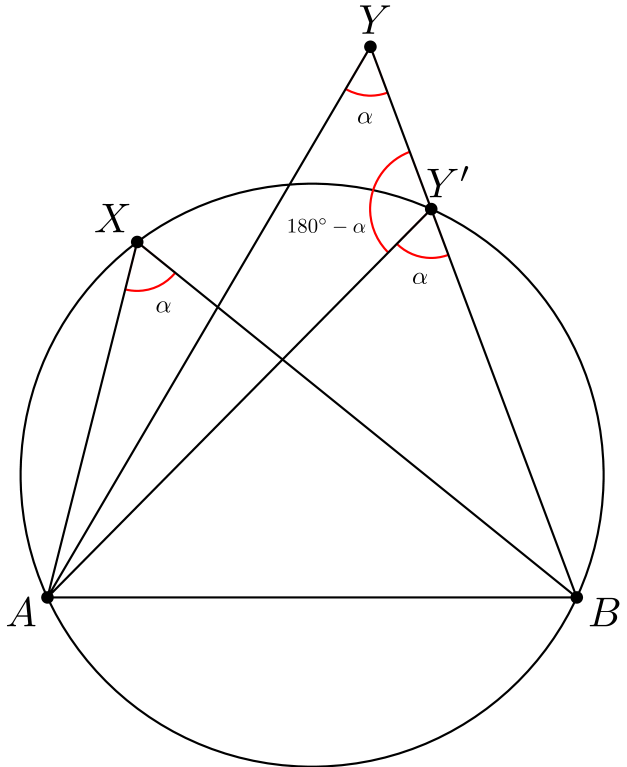
Kuva 9: Kolmion \(AYY'\) yksi kulma on \(0\) astetta, mikä ei käy.

Vastaavalla päättelyllä todetaan, että \(Y\) ei voi olla ympyrän sisäpuolella. (Yksityiskohtia ei käydä läpi tässä.) Siis \(Y\) on ympyrän kehällä, ja todistus on valmis.

6.5 Vastakkaiset kulmat

Kuten kehäkulmalauseessa, voidaan nytkin miettiä tilannetta, jossa \(X\) ja \(Y\) ovat eri puolilla janaa \(AB\). Voisi kuvitella, että myös tässä tapauksessa kehäkulmalausetta voi soveltaa toiseen suuntaan: jos kulmien summa on \(180\) astetta, niin sitten pisteet ovat saman ympyrän kehällä.

Lause 6.3 (Kehäkulmalauseen toinen suunta vastakkaisille kulmille) Olkoot \(A, B, X\) ja \(Y\) pisteitä. Oletetaan, että \(X\) ja \(Y\) ovat eri puolilla janaa \(AB\) ja että \(\angle AXB + \angle BYA = 180^{\circ}\). Tällöin pisteet \(A, B, X\) ja \(Y\) ovat saman ympyrän kehällä.

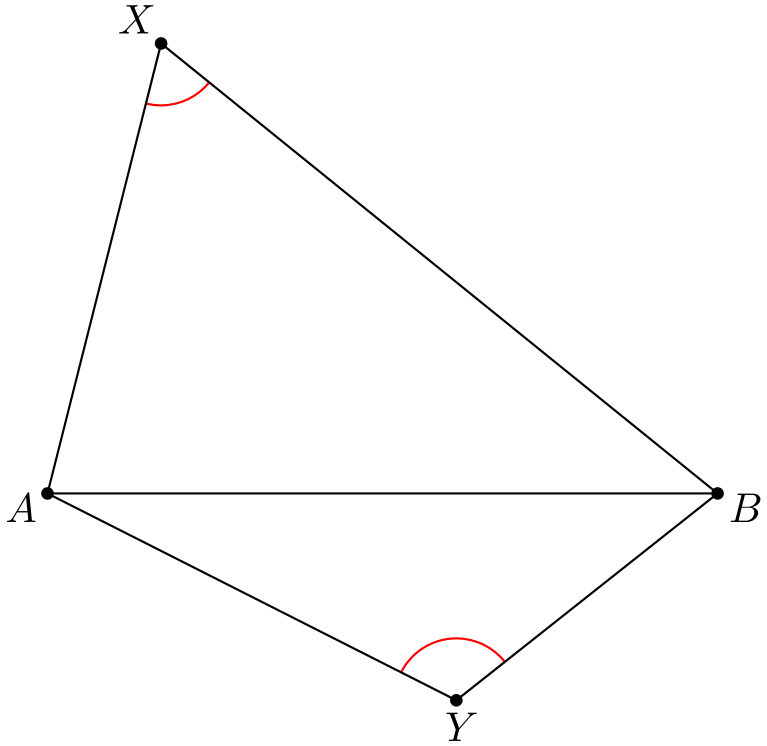
Todistus on käytännössä sama kuin tapauksessa, jossa \(X\) ja \(Y\) ovat samalla puolella janaa \(AB\). Tämän vuoksi alla esitetään vain tiivis kuvaus todistuksen kulusta.

Piirretään ympyrä pisteiden \(A, X\) ja \(B\) kautta. Piste \(Y\) ei voi olla tämän ympyrän ulkopuolella, koska muuten tutkimalla janan \(BY\) ja ympyrän leikkauspistettä ja käyttämällä kehäkulmalauseen versiota vastakkaisille kulmille saataisiin kolmio, jossa on nollan asteen kulma. Vastaavalla päättelyllä \(Y\) ei voi olla ympyrän sisäpuolella. Täten \(Y\) on ympyrän kehällä.

6.6 Tehtäviä

Kehäkulmalause-teksti ja tämä teksti muodostavat yhtenäisen kokonaisuuden, joka kertoo, miten ympyrät ja kulmaehdot liittyvät toisiinsa. Tietyt kulmaehdot toteutuvat täsmälleen silloin, kun pisteet ovat samalla ympyrällä.

Tämä aihe on vahvasti läsnä alla olevissa tehtävissä. Lisäksi tehtävät toimivat harjoituksena kulmien laskemiselle.

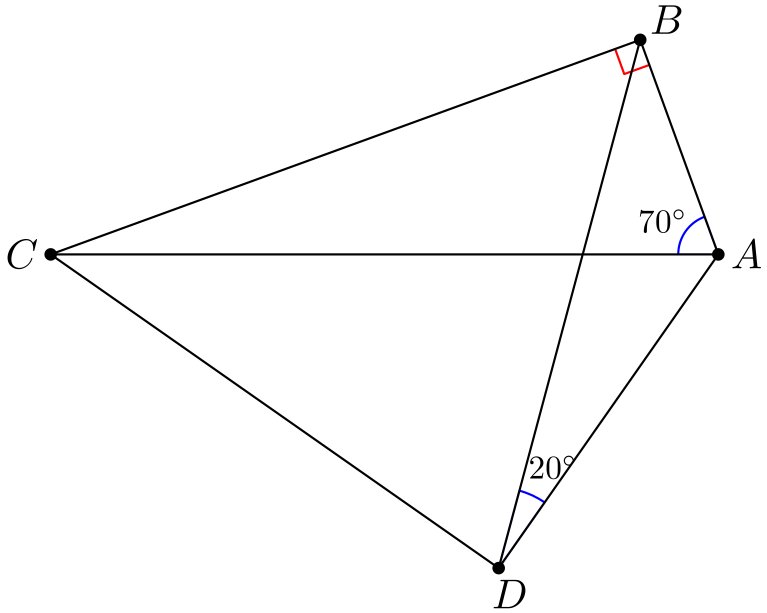
Tehtävä 1. Kuvassa on nelikulmio \(ABCD\). Tiedetään, että \(\angle CBA = 90^{\circ}\), \(\angle BAC = 70^{\circ}\) ja \(\angle ADB = 20^{\circ}\). Kuinka suuri on kulma \(\angle BDC\)?

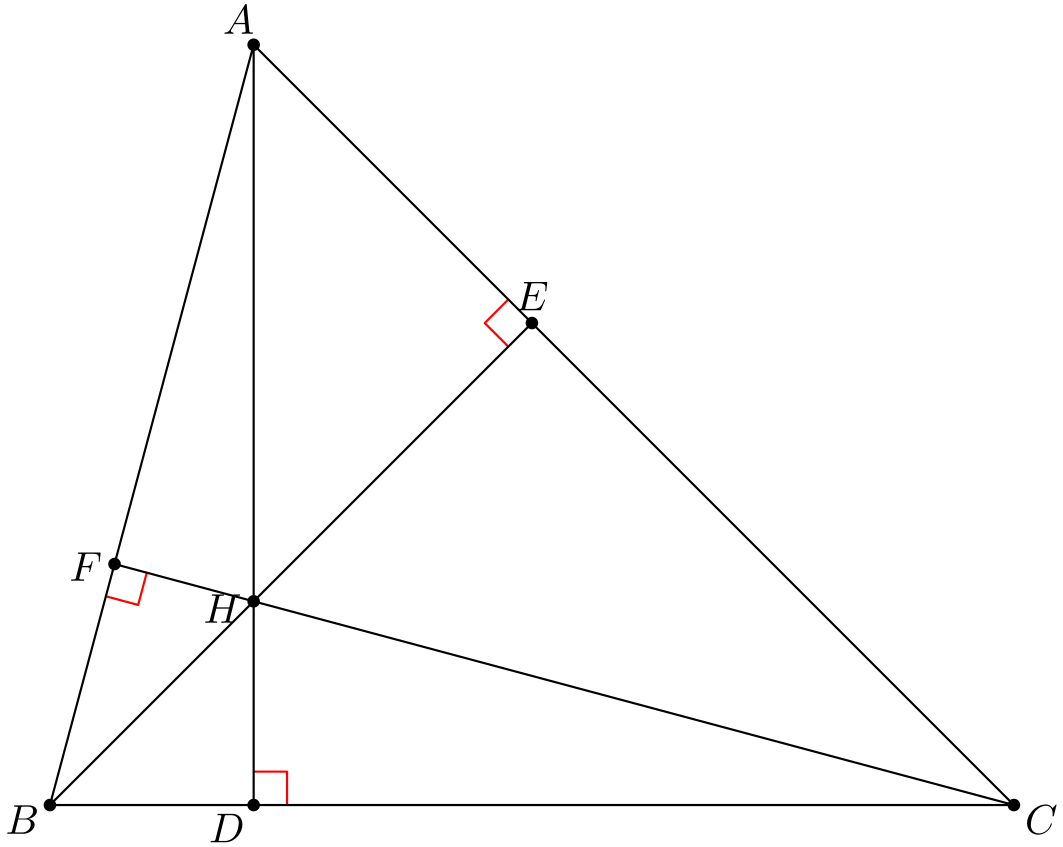
Tehtävä 2. Kuvassa on kolmio \(ABC\) ja korkeusjanat \(AD\), \(BE\) ja \(CF\). Korkeusjanat leikkaavat pisteessä \(H\) (kuten todistettiin Kehäkulmalause-tekstin tehtävässä 7). Kuviossa on peräti kuusi jännenelikulmiota. Mitkä ne ovat?

Tehtävä 3. Jatketaan edellisen tehtävän kuviosta. Osoita, että \(H\) on kolmion \(DEF\) kulmanpuolittajien leikkauspiste. Toisin sanoen osoita, että jana \(EH\) puolittaa kulman \(\angle FED\) (ja vastaavasti symmetriset tapaukset).

Tehtävä 4. Kolmion \(ABC\) sivulla \(BC\) on piste \(D\), sivulla \(AC\) piste \(E\) ja sivulla \(AB\) piste \(F\). Olkoon \(M\) kolmioiden \(AEF\) ja \(BDF\) ympärysympyröiden leikkauspisteistä se, joka ei ole \(F\). Osoita, että pisteet \(C, E, M\) ja \(D\) ovat samalla ympyrällä.

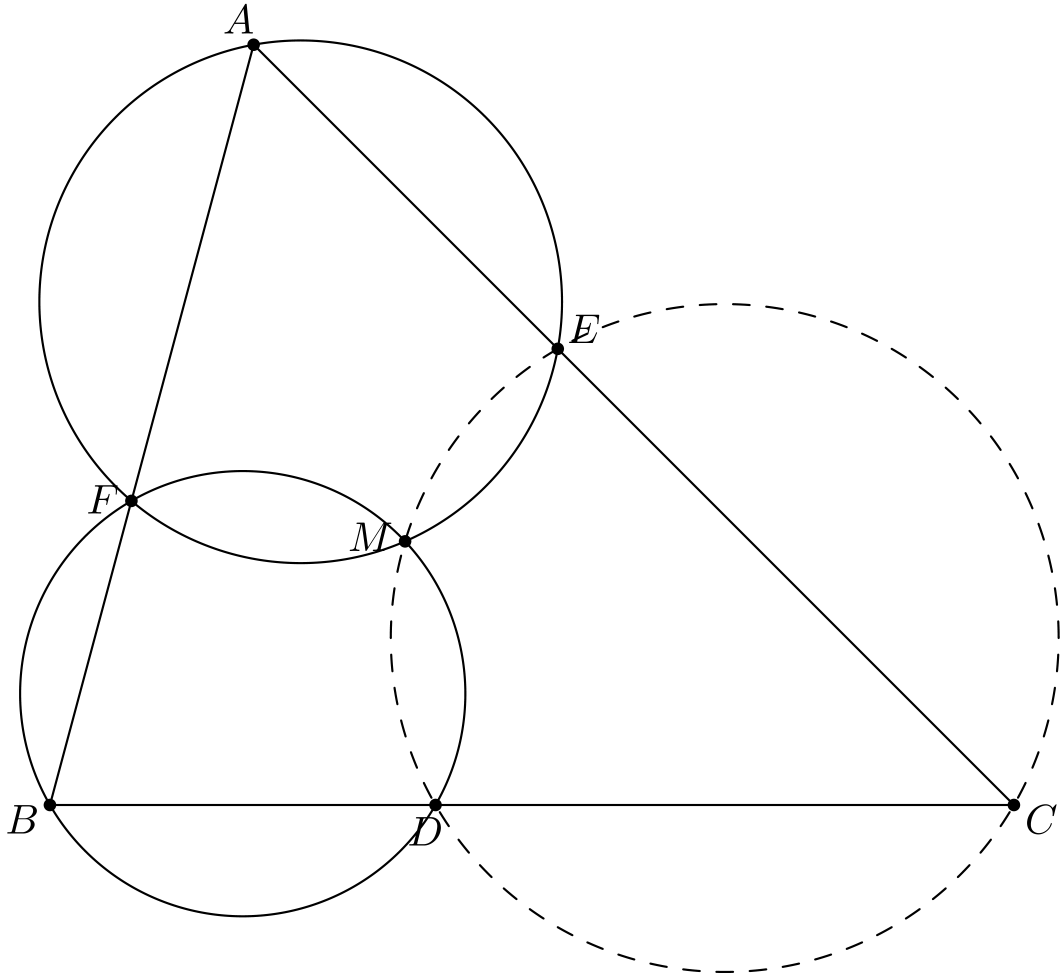
(Toisin sanoen kolmioiden \(AEF\), \(BDF\) ja \(CDE\) ympärysympyrät leikkaavat samassa pisteessä \(M\).)

Tehtävä 5. Tekstissä osoitettiin, että mille tahansa kolmiolle \(ABC\) on olemassa (tasan yksi) ympyrä, joka kulkee kunkin pisteen \(A, B\) ja \(C\) kautta. Tämä tehtiin tutkimalla pisteiden välisten janojen keskinormaaleja.

Muuntele todistuksen ideoita ja osoita, että mille tahansa kolmiolle \(ABC\) on olemassa (tasan yksi) ympyrä, joka sivuaa kutakin janoista \(AB, BC\) ja \(CA\).

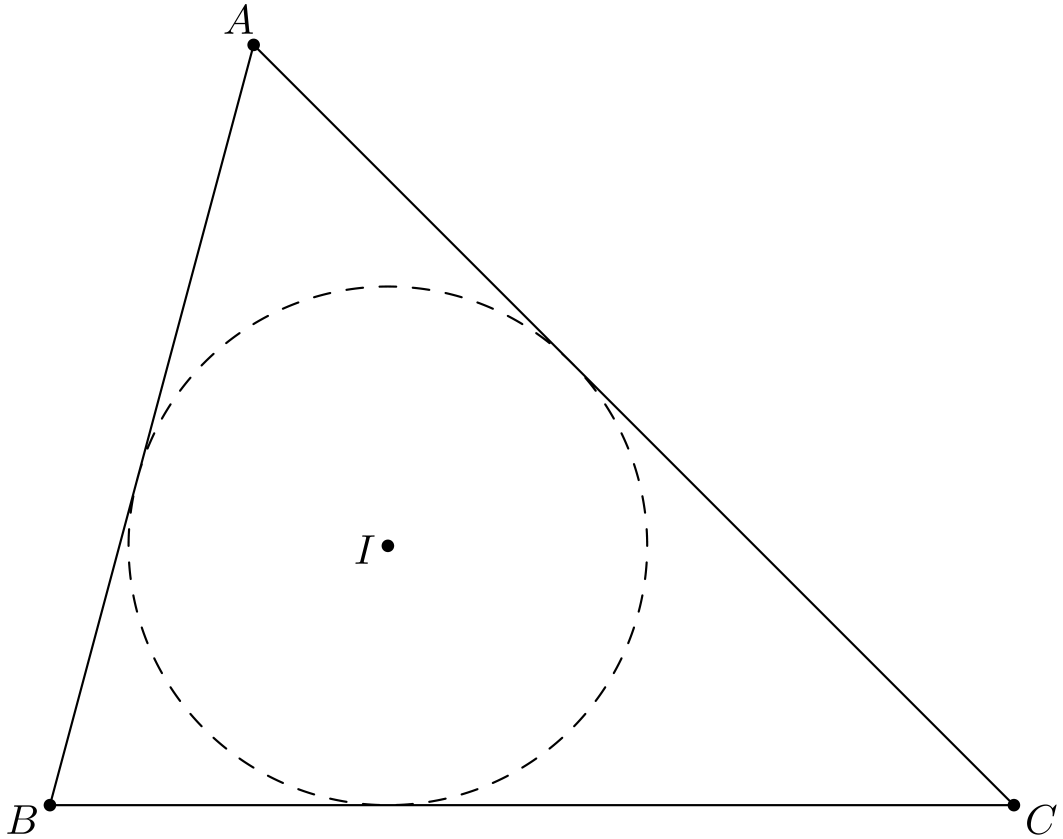
(Tätä ympyrää kutsutaan kolmion \(ABC\) sisäympyräksi tai sisään piirretyksi ympyräksi. Se on suurin ympyrä, joka mahtuu kolmion \(ABC\) sisään.)