17 Pelit

Tekijä

Olli Järviniemi

17.1 Johdanto

Matemaattisissa peleissä on usein kaksi pelaajaa, jotka pelaavat vuorotellen, ja peli päättyy jommankumman pelaajan voittoon (tai tasapeliin). Tässä tekstissä käydään läpi esimerkkejä peleistä ja esitetään yleisimpiä ideoita pelitehtävien ratkaisemiseksi.

17.2 Voitto- ja häviötilat

Tehtävä 17.1 Anna ja Bella pelaavat peliä. Pöydällä on \(100\) tikun kasa. Anna aloittaa, ja pelaajat poistavat kasasta vuorotellen yhden tai kaksi tikkua. Se, jonka siirron jälkeen kasa on tyhjä, voittaa. Kumpi pelaajista voittaa, kun molemmat pelaavat parhaalla mahdollisella tavalla?

Mahdollisia pelistrategioita on tietysti aivan liikaa käytäväksi läpi. Asian helpottamiseksi voidaan tutkia tapauksia, joissa \(100\) tikun sijasta pöydällä on vähemmän tikkuja. Pienistä tapauksista voi nimittäin saada ideoita, jotka auttavat isoissa tapauksissa (kuten tekstissä Induktiivinen päättely huomattiin). Alla on listattu voittaja ja pelin kulku, kun tikkuja on aluksi enintään kuusi.

\(1\) tikku: Anna voittaa poistamalla tikun.
\(2\) tikkua: Anna voittaa poistamalla tikut.
\(3\) tikkua: Bella voittaa. Riippumatta Annan siirrosta Bella voi vuorollaan tyhjentää kasan.
\(4\) tikkua: Anna voittaa poistamalla yhden tikun. Riippumatta Bellan siirrosta Anna voi seuraavalla vuorollaan tyhjentää kasan.
\(5\) tikkua: Anna voittaa poistamalla kaksi tikkua. Riippumatta Bellan siirrosta Anna voi seuraavalla vuorollaan tyhjnetää kasan.
\(6\) tikkua: Bella voittaa. Riippumatta Annan siirrosta Bella voi pelata niin, että pöydällä on hänen siirtonsa jälkeen \(3\) tikkua. Tällöin riippumatta Annan siirrosta Bella voi vuorollaan tyhjentää kasan.

Listauksen jatkaminen pidemmälle onnistuu, mutta tämä vaatii hieman miettimistä. Ensimmäinen tarvittava idea on, että kullakin tikkumäärällä on kätevä puhua siitä, voittaako aloittaja vai ei. Kutsutaan voittotiloiksi tiloja, joissa aloittaja voittaa, ja häviötiloiksi tiloja, joissa aloittaja häviää. Edellä siis \(1, 2, 4\) ja \(5\) ovat voittotiloja ja \(3\) ja \(6\) häviötiloja.

Seuraavat huomiot ovat avainasemassa.

Jos nykyisellä tikkumäärällä voidaan tehdä siirto, jolla päästään häviötilaan, niin nykyinen tila on voittotila.
Jos näin ei voida tehdä, niin nykyinen tila on häviötila.

Tapauksessa (i) aloittaja nimittäin voittaa tekemällä siirron, jonka jälkeen ollaan häviötilassa. Nyt siirtovuoro on vaihtunut ja häviötilan määritelmän nojalla vuorossa oleva pelaaja häviää. Tapauksessa (ii) riippumatta tehdystä siirrosta vastustajan vuorolla ollaan voittotilassa, joten vastustaja voittaa parhaalla mahdollisella tavalla pelatessaan.

Näillä eväillä taulukointia voi jatkaa pidemmälle:

\(1\) tikku: Voittotila
\(2\) tikkua: Voittotila
\(3\) tikkua: Häviötila, koska voidaan siirtyä vain voittotiloihin \(1\) ja \(2\)
\(4\) tikkua: Voittotila, koska voidaan siirtyä häviötilaan \(3\)
\(5\) tikkua: Voittotila, koska voidaan siirtyä häviötilaan \(3\)
\(6\) tikkua: Häviötila, koska voidaan siirtyä vain voittotiloihin \(4\) ja \(5\)
\(7\) tikkua: Voittotila, koska voidaan siirtyä häviötilaan \(6\)
\(8\) tikkua: Voittotila, koska voidaan siirtyä häviötilaan \(7\)
\(9\) tikkua: Häviötila, koska voidaan siirtyä vain voittotiloihin \(7\) ja \(8\)

Säännönmukaisuus on selvä: voitto- ja häviötilat ovat VVHVVHVVHVVH…, eli kolmella jaolliset tikkumäärät ovat häviötiloja ja muut ovat voittotiloja. Täten \(100\) tikulla Anna voittaa, kun molemmat pelaajat pelaavat parhaalla mahdollisella tavalla.

Voitto- ja häviötilat kertovat myös, millä strategialla Anna voittaa. Anna poistaa kasasta aluksi yhden tikun päästäkseen häviötilaan \(99\). Nyt riippumatta Bellan siirrosta Anna voi aina poistaa tikkuja niin, että hänen siirtonsa jälkeen kasassa on kolmella jaollinen määrä tikkuja (jos Bella poistaa yhden tikun, Anna poistaa kaksi, ja jos Bella poistaa kaksi tikkua, Anna poistaa yhden). Ennen pitkää päädytään tilanteeseen, jossa on Bellan vuoro ja kasassa on \(3\) tikkua. Selvästikin Anna voittaa tämän tilanteen.

Kommentti. Voitto- ja häviötilojen taulukointi on erityisen toimiva taktiikka silloin, kun pelissä on hyvin vähän mahdollisia tiloja ja niiden välillä on vain vähän yhteyksiä. Esimerkiksi tässä tehtävässä tutkittavia tiloja on \(100\) ja jokaisesta tilasta on yhteys vain kahteen pienempään tilaan. Pelin tiloja vastaava verkko on siis yksinkertainen: siinä on hyvin vähän kaaria ja ylipäätään verkon rakenne on selkeä.

Sen sijaan monissa oikean elämän lautapeleissä, kuten shakki ja go, tiloja on valtavia määriä, yhteyksiä tilojen välillä on paljon enemmän ja verkon rakenne on monimutkaisempi. Näitä pelejä tutkitaankin hyvin eri tavalla kuin voitto- ja häviötilojen kautta.

17.3 Symmetria

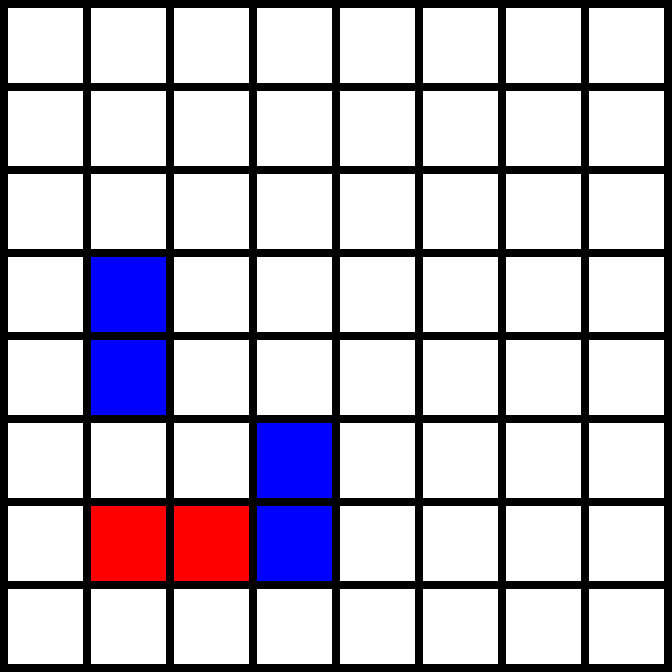
Tehtävä 17.2 Anna ja Bella pelaavat peliä \(8 \times 8\) -laudalla. Anna aloittaa. Pelaajat laittavat vuorotellen \(2 \times 1\) -dominopalikan laudalle niin, että palikka peittää täsmälleen kaksi ruutua eikä mene minkään muun palikan päälle. Palikan saa laittaa pysty- tai vaakasuuntaan. Peli loppuu, kun tällaisia siirtoja ei enää pystytä tekemään. Viimeisen siirron tehnyt voittaa. Kumpi pelaajista voittaa, kun molemmat pelaavat parhaalla mahdollisella tavalla?

Yksi mahdollinen tapa, miten peli on voinut alkaa, kun Anna pelaa sinisillä ja Bella punaisilla.

Tähän peliin ei voitto- ja häviötilojen laskeminen toimi: tiloja on aivan liikaa käytäväksi läpi.

Ratkaisu on hyvin yksinkertainen, kun sen keksii. Bella voittaa. Bellan strategia on aina peilata Annan siirto, eli pelata palikka sellaiseen kohtaan, joka on symmetrinen keskipisteen yli Annan palikkaan nähden.

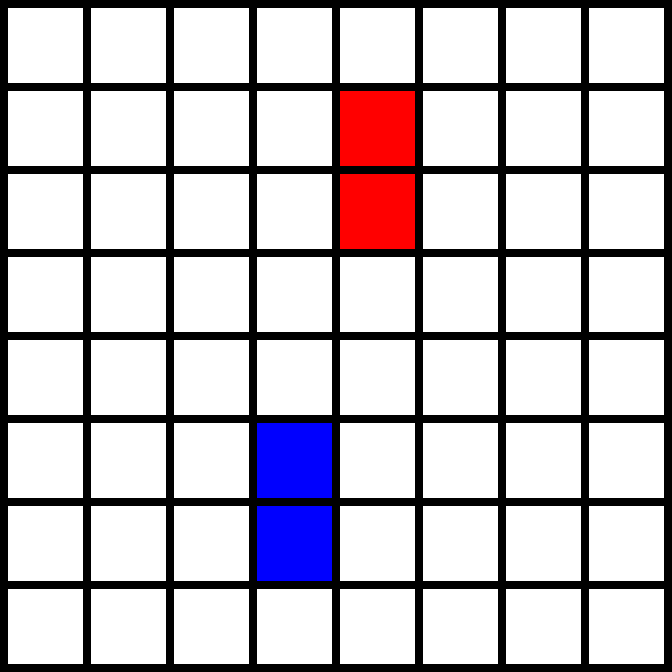
Bella peilaa Annan siirrot laudan keskipisteen suhteen.

Symmetrian vuoksi Bellan siirto ei koskaan mene minkään jo laudalla olevan palikan päälle, koska edellisellä vuorolla Annan siirto on ollut sallittu. Täten Bella voi aina pelata siirron Annan siirron jälkeen, joten Bella voittaa.

17.4 Yleiset huomiot

Tietystikään kaikki peliteorian tehtävät eivät ratkea vain taulukoimalla voittotiloja tai käyttämällä symmetriaa. Otetaan kohtalaisen vaikea esimerkki, jossa tarvitaan luovuutta ja ongelmanratkaisutaitoja.

Tehtävä 17.3 Anna ja Bella pelaavat peliä \(100 \times 100\) -laudalla. Pelaajat valitsevat jonkin laudan ruuduista. Anna aloittaa. Peli päättyy, kun kukin laudan ruuduista on valittu. Anna voittaa, jos hän saa valittua jonkin \(2 \times 2\) -neliön kaikki ruudut. Bella voittaa, jos hän saa estettyä tämän. Kummalla pelaajalla on voittostrategia?

On hyvä idea aluksi yrittää selvittää, kumpi pelaajista voittaa. Pelataan siis itseämme vastaan. Alla on pelin kulusta esimerkki, jossa molemmat pelaavat jossain määrin järkevästi. Anna pelaa punaisilla ja Bella mustilla, ja Bella yrittää estää punaisen \(2 \times 2\) -neliön syntymisen. Lauta on käytännön syistä piirretty \(5 \times 5\) -kokoisena.

Peli ei ole vielä selvä (jos lauta jatkuisi \(5 \times 5\) -alueen ulkopuolelle), mutta alkaa vaikuttamaan siltä, että Bella saa ympäröityä Annan punaiset ruudut riittävän hyvin. Lähdetään siis siitä ajatuksesta, että Bella voittaa.

Miten voidaan todistaa, että Bella voittaa? Tuntuu siltä, että jos kaksi fiksua ihmistä pelaavat peliä, niin Bellan roolissa oleva voittaa, mutta ei ole helppoa selittää miten Bella todella voittaa. ”Bella voittaa pelaamalla järkeviä siirtoja” ei ole kovin vankka perustelu.

Ongelmallista on, että pelissä on valtava määrä tiloja, joten käytännössä ei ole mahdollista kirjoittaa erikseen Bellan siirtoa kullekin mahdolliselle pelin tilalle. Tarvitsemme jonkin yksinkertaisen tavan kuvailla Bellan strategiaa: kun pelilauta näyttää tältä, pelataan näin.

Yksi oleellinen kysymys on, kuinka monia tekijöitä strategia ottaa huomioon. Toisaalta relevantteja tekijöitä on melko paljon, koska käytännössä jokainen laudan ruuduista on tärkeä, mutta toisaalta mitä enemmän asioita otamme huomioon, sitä monimutkaisemmaksi strategiat menevät.

Voidaan kuitenkin yrittää keksiä yksinkertaisia strategioita, jotka ottavat vain vähän tekijöitä huomioon. Otetaan vaikkapa huomioon vain se, mihin ruutuun Anna on pelannut viimeisellä vuorollaan.

Miten vastaamme Annan siirtoon? Niin yksinkertainen strategia kuin ”pelataan suoraan Annan oikealle puolelle” ei toimi. Voisimme yrittää jotain hieman monimutkaisempaa strategiaa, jossa siirto riippuu siitä, miltä Annan valitseman ruudun lähiympäristö näyttää. Tämä menee kuitenkin nopeasti melko vaikeaksi, koska tapauksia on niin paljon.

Yritetään keksiä strategia, joka ei riipu ruudun lähiympäristöstä, vaan ainoastaan valitusta ruudusta. Toisin sanoen mietitään strategioita muotoa ”jos Anna jossain kohtaa peliä pelaa tähän ruutuun, pelataan itse tuohon ruutuun”. Haluamme valita vastauksemme niin, että se estää Annaa luomasta \(2 \times 2\) -neliötä, joten valitsemamme ruudun kannattaa olla hyvin lähellä Annan ruutua.

Kokeilemalla hieman tällaisia ideoita päädytään seuraavaan ratkaisuun. Jaetaan lauta \(2 \times 1\) -laattoihin alla olevan kuvan mukaisesti. Aina kun Anna pelaa laatan jompaankumpaan ruutuun, Bella valitsee seuraavalla vuorollaan laatan toisen ruudun. Koska jokainen \(2 \times 2\) -neliö sisältää vähintään yhden kokonaisen laatan, estää tämä Annaa muodostamasta \(2 \times 2\) -neliötä.

\(8 \times 8\) -laudan jako \(2 \times 1\) -laattoihin niin, että mikä tahansa \(2 \times 2\) -neliö peittää yhden laatoista.

Kommentti. Bellan strategia on hyvin lokaali: Bellan ei tarvitse muistaa mitä pelissä on aiemmin tapahtunut tai tarkastella koko laudan tilaa vaan ainoastaan tietää, mihin ruutuun Anna on viimeksi pelannut. On hyvä lähteä miettiminen tällaisista lokaaleista strategioista, koska ne ovat yksinkertaisempia.

Lokaalin idean vastakohta on globaali argumentti, joka katsoo kokonaiskuvaa. Näihin pureudutaan myöhemmin edistyneemmässä tekstissä.

17.5 Tehtäviä

Tehtävä 1. Anna ja Bella pelaavat peliä \(100 \times 101\) -laudalla. Laudan vasemmassa ylänurkassa on pelimerkki. Anna aloittaa. Pelaajat liikuttavat pelimerkkiä vuorotellen jonkin määrän ruutuja alaspäin tai jonkin määrän ruutuja oikealle. (Pelimerkkiä täytyy liikuttaa vähintään yhden ruudun verran.) Peli päättyy, kun pelimerkki on laudan oikeassa alanurkassa. Viimeisen siirron tehnyt voittaa. Kumpi pelaaja voittaa, kun molemmat pelaavat optimaalisella tavalla?

Tehtävä 2. Liitutaululle on kirjoitettu luku \(100\). Anna ja Bella pelaavat seuraavanlaista peliä. Anna aloittaa. Pelaajat vähentävät vuorotellen taululla olevasta luvusta \(x\) jonkin luvun, joka jakaa luvun \(x\) ja joka on pienempi kuin \(x\). (Esimerkiksi jos taululla on luku \(12\), siitä saa vähentää jonkin luvuista \(1, 2, 3, 4, 6\).) Se pelaaja voittaa, jonka siirron jälkeen taululla on luku \(1\). Kumpi pelaajista voittaa, kun molemmat pelaavat optimaalisella tavalla?

Tehtävä 3. Anna ja Bella pelaavat peliä \(100 \times 1\) -laudalla. Anna aloittaa. Pelaajat laittavat vuorotellen laudalle \(2 \times 1\) -dominopalikan. Palikat eivät saa mennä päällekkäin tai laudan ulkopuolelle. Peli päättyy, kun tällaisia siirtoja ei enää voi tehdä. Viimeisen siirron tehnyt voittaa. Kumpi pelaajista voittaa, kun molemmat pelaavat optimaalisella tavalla?

Tehtävä 4. Anna ja Bella pelaavat peliä \(100 \times 1\) -laudalla. Anna aloittaa. Pelaajat valitsevat vuorotellen jonkin laudan ruuduista. Pelaaja ei saa valita jo aiemmin valittua ruutua. Annan tavoite on saada valittua jotkin kolme peräkkäistä ruutua. Bellan tavoite on estää tämä. Peli päättyy, kun kaikki laudan ruudut on valittu. Kumpi pelaajista voittaa, kun molemmat pelaavat optimaalisella tavalla?

Tehtävä 5. Anna ja Bella pelaavat peliä \(100 \times 100\) -laudalla. Anna aloittaa. Pelaajat valitsevat vuorotellen jonkin laudan ruuduista. Pelaaja ei saa valita jo aiemmin valittua ruutua. Annan tavoite on saada valittua jotkin \(k\) peräkkäistä ruutua (pysty- tai vaakasuunnassa). Bellan tavoite on estää tämä. Peli päättyy, kun kaikki laudan ruudut on valittu. Osoita, että

jos \(k = 4\), niin Annalla on voittostrategia
jos \(k = 5\), niin Bellalla on voittostrategia.