12 Polynomit II
12.1 Johdanto
Jatkamme aiemmassa tekstissä aloitettua polynomien käsittelyä. Todistamme lauseen polynomin esittämisestä nollakohtiensa avulla ja annamme tulokselle sovelluksia. Esitämme myös pari tulosta, jotka kertovat, mitä ominaisuuksia polynomien nollakohdilla on.
12.2 Nollakohtaesitys
Palautetaan mieleen edellisen tekstin lause:
Todistuksen idea perustuu polynomien jakoyhtälön soveltamiseen. Jakoyhtälö nimittäin antaa seuraavan tuloksen.
Apulause 12.1 Olkoon \(P(x)\) polynomi, ja olkoon \(\alpha\) polynomin \(P\) nollakohta. Tällöin on olemassa polynomi \(Q(x)\), jolla \[P(x) = (x - \alpha)Q(x).\]
Apulauseen todistus. Käytetään jakoyhtälöä polynomeille \(P(x)\) ja \(x - \alpha\). Jakoyhtälön nojalla on olemassa polynomit \(Q(x)\) ja \(R(x)\), joilla \[P(x) = (x - \alpha)Q(x) + R(x)\] ja joilla polynomin \(R(x)\) aste on pienempi kuin polynomin \(x - \alpha\). Täten \(R(x)\) on vakiopolynomi. Toisaalta asettamalla yllä olevaan yhtälöön \(x = \alpha\) saadaan \(R(\alpha) = 0\), eli \(R\) on nollapolynomi eli \(P(x) = (x - \alpha)Q(x)\).
Lauseen todistus. Ideana on käyttää apulausetta toistuvasti. Käyttämällä ensin lemmaa nollakohdalle \(\alpha_1\) löydetään jokin polynomi \(Q_1(x)\), jolla \[P(x) = (x - \alpha_1)Q_1(x).\] Polynomilla \(Q_1\) on vielä nollakohdat \(\alpha_2, \alpha_3, \ldots , \alpha_n\). Käyttämällä lemmaa polynomille \(Q_1(x)\) ja sen nollakohdalle \(\alpha_2\) saadaan \[Q_1(x) = (x - \alpha_2)Q_2(x).\] Polynomilla \(Q_2\) on vielä nollakohdat \(\alpha_3, \alpha_4, \ldots , \alpha_n\). Jatketaan vastaavasti.
Toistamalla tätä prosessia päästään polynomiin \(Q_{n+1}(x)\), jolla ei enää ole nollakohtia, eli \(Q_{n+1}(x)\) on vakiopolynomi. Purkamalla saadut yhtälöt saadaan \[P(x) = (x - \alpha_1)(x - \alpha_2) \cdots (x - \alpha_n)Q_{n+1}(x).\] Vertaamalla termin \(x^n\) kertoimia yhtälön vasemmalla ja oikealla puolella saadaan, että vakiopolynomin \(Q_{n+1}(x)\) arvo on \(a_n\).
12.3 Nollakohtaesityksen hyötyjä
12.3.1 Yhtäläisyydet alkutekijähajotelmaan
Polynomin nollakohtaesityksellä on joitain samankaltaisuuksia kokonaislukujen esittämiseen alkulukujen tulona. Esimerkkejä:
- Jokainen positiivinen kokonaisluku voidaan esittää yksikäsitteisellä tavalla alkulukujen tulona. Vastaavasti jokainen polynomi voidaan esittää muotoa \(x - \alpha\) olevien polynomien tulona (kerrottuna jollakin vakiolla).
- Jos on annettu kahden luvun alkutekijähajotelma, on näiden kahden luvun tulon alkutekijähajotelma hyvin helppo laskea. (Tulon alkutekijähajotelmassa jokainen alkuluku esiintyy yhtä monta kertaa kuin lukujen alkutekijähajotelmissa yhteensä). Vastaavasti jos on annettu kahden polynomin esitys nollakohtien avulla, on näiden kahden polynomin tulon nollakohtaesitys hyvin helppoa laskea. (Tulon esityksessä jokainen termi muotoa \(x - \alpha\) esiintyy yhtä monta kertaa kuin polynomien esityksissä yhteensä.)
- Jos on annettu kahden luvun alkutekijähajotelma, on alkutekijähajotelmista hyvin helppo nähdä, jakaako toinen luku toisen. (Näin on täsmälleen silloin, kun jaettavassa kukin alkuluku esiintyy vähintään yhtä monta kertaa kuin jakajassa.) Vastaavasti jos on annettu kahden polynomin esitys nollakohtien avulla, on hyvin helppo nähdä, jakaako toinen polynomi toisen. (Näin on täsmälleen silloin, kun jaettavassa kukin termi \(x - \alpha\) esiintyy vähintään yhtä monta kertaa kuin jakajassa.)
Otetaan tähän viimeiseen pointtiin liittyen esimerkki.
Helppo tapa vastata kysymykseen on laskea polynomien jakolasku, mutta tämä olisi kauhean työlästä. Mietitään jotain fiksumpaa.
Yllä esitetyt pointit ajavat takaa sitä, että ”oikea” tapa miettiä jaollisuutta on nollakohtien kautta. Polynomi \(x^3 + x + 1\) jakaa polynomin \(9x^9 + 7x^7 + 5x^5 + 3x^3 + x\), jos kukin ensimmäisen polynomin nollakohta on myös toisen nollakohta (ja kukin ensimmäisen polynomin kaksinkertainen nollakohta on myös toisen kaksinkertainen nollakohta ja niin edelleen)1, ja muuten ei.
1 On hyvä mainita seuraava nyrkkisääntö: jos valitsemme ”satunnaisen” polynomin, eli arvomme sen asteen ja kertoimet, niin on hyvin epätodennäköistä, että polynomilla on kaksinkertainen nollakohta. Täten yleensä kannattaa aloittaa miettiminen nollakohdista, ja vasta tarpeen tullen miettiä moninkertaisia nollakohtia.
Mitä osaamme sanoa polynomin \(x^3 + x + 1\) nollakohdista? Emme kovinkaan paljoa. Helppoja nollakohtia, kuten \(0, -1, 1, 2, -2, 1/2, \ldots\), ei tunnu löytyvän. Missä nollakohdat edes sijaitsevat? Se huomataan, että välillä \((-1, 0)\) on vähintään yksi nollakohta: polynomi \(x^3 + x + 1\) nimittäin saa arvon \(-1\) pisteessä \(x = -1\) ja arvon \(1\) pisteessä \(x = 0\), joten tässä välissä polynomi saa arvon \(0\), kuten nähdään tarkastelemalla polynomin kuvaajaa.
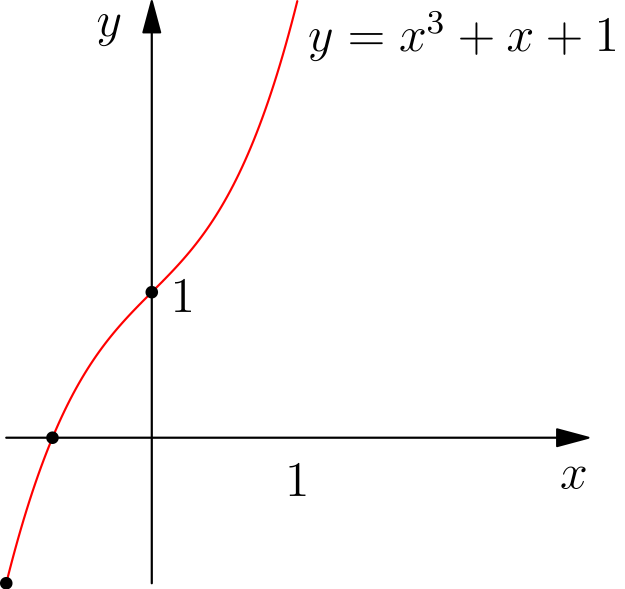
Onko polynomilla \(9x^9 + 7x^7 + 5x^5 + 3x^3 + x\) nollakohtaa välillä \((-1, 0)\)? Ei: jos \(x\) on negatiivinen, niin luvut \(x^9, x^7, x^5, x^3\) ja \(x\) ovat myös negatiivisia, ja polynomin arvo on negatiivinen.
Täten \(9x^9 + 7x^7 + 5x^5 + 3x^3 + x\) ei ole jaollinen polynomilla \(x^3 + x + 1\).
12.3.2 Vietan kaavat
Nollakohtaesityksestä saadaan myös yhteys polynomin kertoimien ja nollakohtien välille.
Tutkitaan toisen asteen polynomia \(ax^2 + bx + c\). Olkoot sen nollakohdat \(\alpha_1\) ja \(\alpha_2\). Nollakohtaesityksen nojalla voidaan kirjoittaa \[ax^2 + bx + c = a(x - \alpha_1)(x - \alpha_2).\] Oikea puoli on kerrottuna auki \[ax^2 - a(\alpha_1 + \alpha_2)x + a\alpha_1\alpha_2.\] Vertailemalla kertoimia saadaan \(b = -a(\alpha_1 + \alpha_2)\) ja \(c = a\alpha_1\alpha_2\), eli toisin sanoen \[\alpha_1 + \alpha_2 = - \frac{b}{a}\] ja \[\alpha_1\alpha_2 = \frac{c}{a}.\] Saamme siis selville polynomin nollakohtien summan ja tulon katsomalla pelkästään polynomien kertoimia!
Toisen asteen yhtälö on vielä kohtalaisen laimea esimerkki, koska toisen asteen yhtälölle on verrattain helppo ratkaisukaava. Idea kuitenkin yleistyy myös korkeamman asteen polynomeille. Esimerkiksi jos \(a, b\) ja \(c\) ovat yhtälön \[x^3 + 2x^2 + 3x + 4 = 0\] ratkaisut, niin nollakohtaesityksestä saadaan \[x^3 + 2x^2 + 3x + 4 = (x - a)(x - b)(x - c).\] Kertomalla taas auki ja vertailemalla kertoimia saadaan \[a + b + c = -2,\] \[ab + bc + ca = 3\] ja \[abc = -4.\] Eli vaikka kolmannen asteen yhtälön ratkaiseminen on vaikeaa, saadaan mm. yhtälön ratkaisujen summa ja tulo selville hyvinkin helposti. Yllä saatuja yhteyksiä polynomin kertoimien ja nollakohtien välille kutsutaan Vietan kaavoiksi.
12.4 Rationaaliset nollakohdat
Olemme puhuneet paljon nollakohdista, muttemme paljoa siitä, miten nollakohdat oikeasti löydetään. Syynä on se, että yleisen polynomiyhtälön ratkaiseminen on vaikeaa. Toisen asteen yhtälö vaatii jo jonkin verran tekemistä ja kolmannen ja neljännen asteen yhtälöt ovat vielä vaikeampia. Viidennen asteen yhtälöstä lähtien ei edes ole olemassa samantyyppistä ratkaisukaavaa kuin pienemmissä tapauksissa.
Edellisessä esimerkkitehtävässä löysimme yhden hyvän idean: muodostamalla sopivia epäyhtälöitä voidaan saada tietoa siitä, kuinka suuria nollakohdat suunnilleen ovat.
Tässä osiossa käsitellään sitä, miltä polynomien rationaaliset nollakohdat näyttävät.
Todistus on melko yksinkertainen. Oletetaan, että \(s/t\) on nollakohta, eli \[a_n\left(\frac{s}{t}\right)^n + a_{n-1}\left(\frac{s}{t}\right)^{n-1} + \ldots + a_1\left(\frac{s}{t}\right) + a_0 = 0.\] Kerrotaan puolittain luvulla \(t^n\). \[a_ns^n + a_{n-1}s^{n-1}t + \ldots + a_1st^{n-1} + a_0t^n = 0.\] Tutkitaan nyt yhtälön termien jaollisuutta luvulla \(s\). Oikea puoli on tietysti jaollinen luvulla \(s\). Vasemmalla puolella kaikki paitsi viimeinen summattava ovat jaollisia luvulla \(s\). Täten viimeisenkin summattavan \(a_0t^n\) tulee olla jaollinen luvulla \(s\). Miettimällä lukujen alkutekijähajotelmia ja käyttämällä tietoa siitä, että \(\frac{s}{t}\) on supistetussa muodossa (eli \(\text{syt}(s, t) = 1\)) saadaan, että \(s\) jakaa luvun \(a_0\).
Vastaavasti tutkimalla jaollisuutta luvulla \(t\) saadaan, että \(t\) jakaa luvun \(a_n\).
12.5 Polynomiepäyhtälö
Käsitellään vielä yhtä aihetta: polynomiepäyhtälö. Tehdään tämä esimerkin kautta.
Tekstin teeman mukaisesti on luontevaa miettiä ensin polynomin nollakohtia. Rationaalisen nollakohdan tulee edellisen tuloksen nojalla olla \(1\) tai \(-1\). Huomataankin, että \(-1\) on nollakohta, ja pienellä työllä saadaan tekijöihinjako \[x^6 + 2x^5 + x^4 - x^3 - x^2 + x + 1 = (x+1)(x^5 + x^4 - x^2 + 1).\]
Huomataan, että \(x = -1\) on edelleen toisen tulontekijän nollakohta.
Tämä ei ole sattumaa. Jos \(-1\) ei olisi toisen tulontekijän nollakohta, muuttuisi polynomin \((x+1)(x^5 + x^4 - x^2 + 1)\) merkki pisteen \(x = -1\) lähellä, koska termin \(x+1\) merkki muuttuisi, mutta termin \(x^5 + x^4 - x^2 + 1\) merkki ei muuttuisi. Me kuitenkin tiedämme, että merkki ei muutu: meitähän pyydetään todistamaan, että polynomi on aina vähintään nolla.
Eli totta kai \(x = -1\) on (vähintään) kaksinkertainen nollakohta. Hyödynnetään tätä. Tästä saadaan jaettua \(x^5 + x^4 - x^2 + 1\) tekijöihin, ja tutkittava polynomi muuttuu muotoon \[(x+1)^2(x^4 - x + 1).\] Koska \((x+1)^2\) on aina vähintään nolla, riittää enää todistaa, että \[x^4 - x + 1 \ge 0.\]
Tämä epäyhtälö vaatii uusia ideoita. Helppoja nollakohtia tai tekijöihinjakoa ei enää löydy. Toteamme kuitenkin samaan tapaan kuin yllä, että jos polynomilla \(x^4 - x + 1\) on reaalisia nollakohtia, niin niiden tulee olla vähintään kaksinkertaisia. Voisi veikata, että kaksinkertaisia nollakohtia ei ehkä enää löydy, eli reaalisia nollakohtia ei enää pitäisi löytyä.
Pystymmekö todistamaan tämän? Kuvitellaan, että \(x\) on reaalinen nollakohta. Mitä luvusta \(x\) voidaan sanoa? Selvästikään \(x\) ei voi olla negatiivinen, koska negatiivisilla \(x\) lausekkeen \(x^4 - x + 1\) arvo on positiivinen. Luku \(x\) ei myöskään voi olla vähintään \(1\), koska tällöin \(x^4 \ge x\) ja pätisi \(x^4 - x + 1 \ge 1\). Kuitenkaan \(x\) ei voi olla väliltä \([0, 1)\), koska tällöin \(-x + 1 > 0\) ja siten myös \(x^4 - x + 1 > 0\).
Siis \(x^4 - x + 1\) on aina positiivinen. Täten \((x + 1)^2(x^4 - x + 1) \ge 0\), mikä todistaa tehtävän epäyhtälön.
12.6 Tehtäviä
Tehtävä 1. Ratkaise yhtälö \(2x^3 - x^2 - 10x + 5 = 0\).
Tehtävä 2.
Todista, että \(\sqrt{2}\) ei ole rationaalinen tutkimalla polynomia \(x^2 - 2\).
Todista, että jos \(n\) on sellainen positiivinen kokonaisluku, että \(\sqrt{n}\) on rationaalinen, niin \(\sqrt{n}\) on kokonaisluku (eli \(n\) on neliöluku).
Tehtävä 3.
- Polynomilla \(P(x)\) pätee \(P(n) = n\) kaikilla kokonaisluvuilla \(n\). Seuraako tästä, että \(P(x) = x\) kaikilla reaaliluvuilla \(x\)?
- Polynomilla \(P(x)\) pätee \(P(n) > n\) kaikilla kokonaisluvuilla \(n\). Seuraako tästä, että \(P(x) > x\) kaikilla reaaliluvuilla \(x\)?
Tehtävä 4. Olkoon \(n\) positiivinen kokonaisluku. Osoita, että \(\text{syt}(2n+1, n^2+1) \le 5\).
Tehtävä 5. Polynomin \(P(x) = x^3 - 3x^2 + 2x - 1\) nollakohdat ovat \(a, b\) ja \(c\). Laske \(a^2 + b^2 + c^2\).
Tehtävä 6. Polynomin \(P(x) = x^3 - 3x^2 + 2x - 1\) nollakohdat ovat \(a, b\) ja \(c\). Anna esimerkki (epävakiosta) polynomista, jonka kertoimet ovat kokonaislukuja ja jolla on luvut \(a^2, b^2\) ja \(c^2\) nollakohtinaan.