33 Primitiivijuurten olemassaolon todistus
\[ \newcommand{\syt}{\text{syt}} \newcommand{\pyj}{\text{pyj}} \]
33.1 Johdanto
Tässä tekstissä todistetaan, että jokaisella alkuluvulla \(p\) on olemassa primitiivijuuri modulo \(p\). Aloitamme parin työkalun esittelyllä ennen kuin pääsemme varsinaisen todistuksen kimppuun.
Todistus on vaikea. Lopussa olevat tehtävät tukevat ideoiden ymmärtämistä. Niitä kannattaa tehdä samalla, kun yrittää sisäistää todistuksen ideoita.
33.2 Lagrangen lause
Todistus tulee hyödyntämään seuraavaa tulosta.
Tilanne on siis sama kuin tavallisessa modulottomassa tapauksessa: polynomilla on enintään asteensa verran nollakohtia. Tulos ei siis ole kovin epäintuitiivinen. Huomaa kuitenkin, että ratkaisuja voi olla alle asteen verran. Esimerkiksi yhtälöllä \(x^2 + 1 \equiv 0 \pmod{3}\) ei ole yhtäkään ratkaisua.
”Tavallisilla luvuilla” vastaavan väitteen voi todistaa käyttämällä polynomien jakoyhtälöä: Jos astetta \(n\) olevalla polynomilla \(P(x)\) on nollakohta \(\alpha\), niin voidaan kirjoittaa \(P(x) = (x - \alpha)Q(x)\) jollain polynomilla \(Q(x)\). Täten jos polynomilla \(P\) olisi vähintään \(n+1\) nollakohtaa \(\alpha_1, \ldots , \alpha_{n+1}\), voitaisiin kirjoittaa \[P(x) = (x - \alpha_1)(x - \alpha_2) \cdots (x - \alpha_n)(x - \alpha_{n+1})R(x)\] jollain polynomilla \(R(x)\). Oikean puolen aste on vähintään \(n+1\) (koska \(R\) ei ole nollapolynomi), kun taas vasemman puolen aste on \(n\). Tämä ei käy.
Sama todistus toimii myös kokonaisluvuilla modulo \(p\). Ainoa epävarma tekijä on, toimiiko polynomien jakoyhtälö. Kuitenkin käymällä läpi polynomien jakoyhtälön todistuksen vaiheet huomataan, että kaikki vaiheista voidaan tehdä myös modulo \(p\). Tämä todistaa väitteen. (Yksityiskohdat sivuutetaan.)
33.3 Fii-funktio
Tätä kutsutaan fii-funktioksi (luvusta \(n\)). Esimerkkejä:
- \(\phi(1) = 1\), koska vain \(x = 1\) toteuttaa ehdot.
- \(\phi(2) = 1\), koska vain \(x = 1\) toteuttaa ehdot.
- \(\phi(3) = 2\), koska ensimmäisen ehdon toteuttavista luvuista \(x = 1, 2, 3\) toisen ehdon toteuttavat \(1\) ja \(2\).
- \(\phi(4) = 2\), koska ensimmäisen ehdon toteuttavista luvuista \(x = 1, 2, 3, 4\) toisen ehdon toteuttavat \(1\) ja \(3\).
- \(\phi(5) = 4\), koska luvuista \(x = 1, 2, 3, 4, 5\) kaikki paitsi \(5\) kelpaavat.
- \(\phi(6) = 2\), koska luvuista \(x = 1, 2, 3, 4, 5, 6\) vain \(1\) ja \(5\) kelpaavat.
- \(\phi(7) = 6\), koska luvuista \(x = 1, 2, 3, 4, 5, 6, 7\) kaikki paitsi \(7\) kelpaavat.
- \(\phi(8) = 4\), koska luvuista \(x = 1, 2, 3, 4, 5, 6, 7, 8\) täsmälleen parittomat kelpaavat.
Miksi haluamme tutkia fii-funktiota? Mietitään aiemmin nähtyä kuviota yhteenlaskusta modulo \(12\):
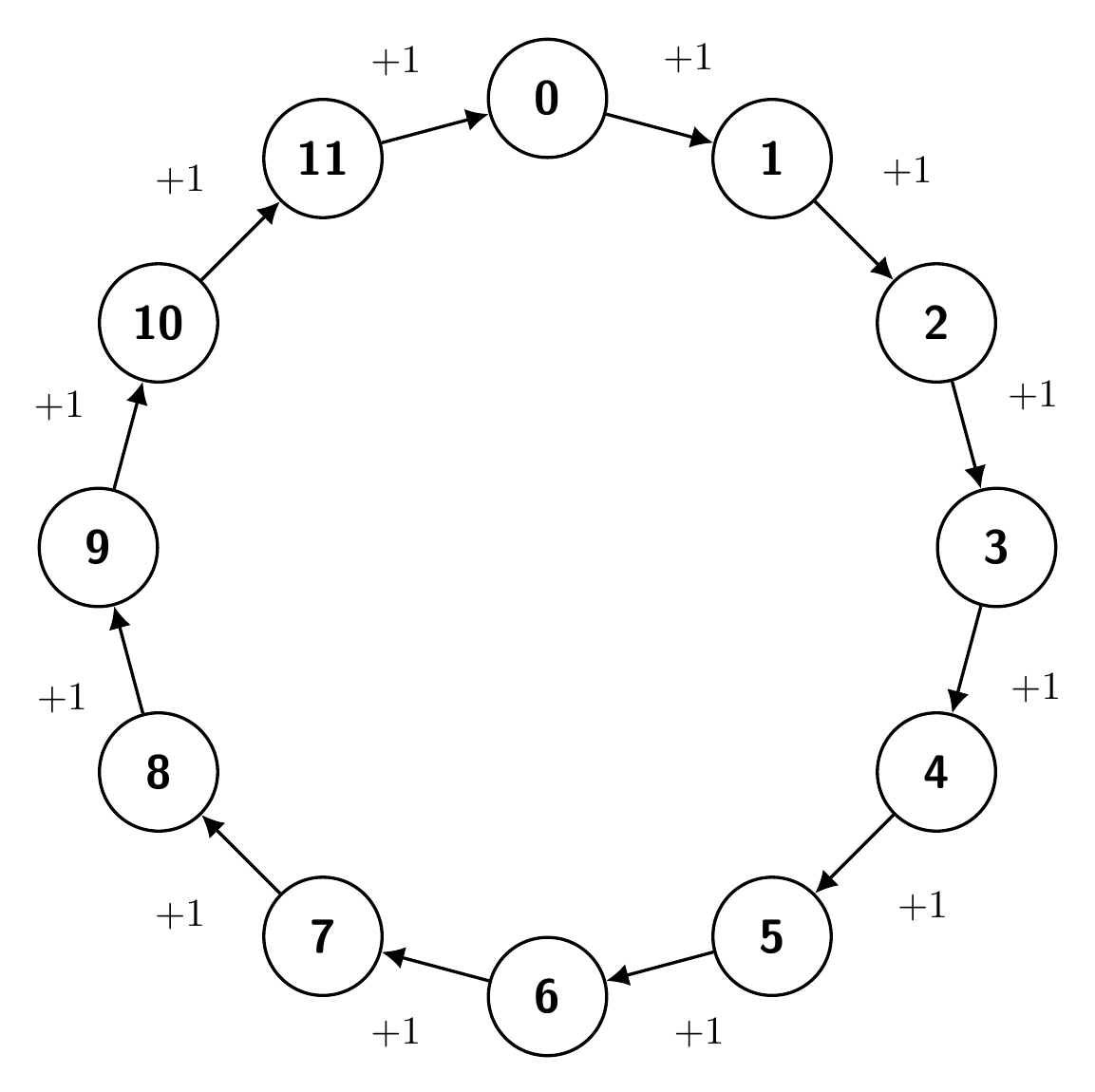
Valitaan jokin luku \(x\) ja tutkitaan lukuja \(x, 2x, 3x, \ldots , 12x\). Joissain tapauksissa nämä luvut sisältävät kaikki luvuista \(0, 1, 2, \ldots , 11\) modulo \(12\). Yksi tällainen tapaus on tietysti \(x = 1\), mutta esimerkiksi luvulla \(x = 5\) on myös tämä ominaisuus: jos aloitamme ringin luvusta \(5\) ja otamme viiden askeleen hyppyjä eteenpäin, saadaan luvut \[5, 10, 3, 8, 1, 6, 11, 4, 9, 2, 7, 0.\] Joissakin tapauksissa näin ei kuitenkaan käy. Jos valitaan esimerkiksi luku \(4\), saadaan vain luvut \(4, 8, 0\).
Nähdään, että luvut \(x, 2x, \ldots , 12x\) käyvät kaikki luvut läpi täsmälleen silloin, kun \(\text{syt}(x, 12) = 1\). Fii-funktio siis kertoo, kuinka monta kuvatunlaista lukua on. Voidaan laskea, että \(\phi(12) = 4\), koska luvuista \(1, 2, \ldots , 12\) luvun \(12\) kanssa yhteistekijättömiä ovat \(1, 5, 7\) ja \(11\).
Tämä on syy sille, minkä takia käsittelemme fii-funktiota. Yllä tutkittiin ominaisuuksia yhteenlaskun näkökulmasta, mutta alla tulemme käyttämään samanlaisia ideoita myös kertolaskulle.
33.4 Eräs fii-funktion ominaisuus
Fii-funktiosta voisi sanoa paljonkin, mutta tarvitsemme vain pari ominaisuutta. Ensimmäinen on helppo.
Jos \(n\) on positiivinen kokonaisluku, niin \(\phi(n) \ge 1\).
Todistus: Voidaan valita \(x = 1\): tällöin \(1 \le x \le n\) ja \(\text{syt}(x, n) = 1\).
Sitten vaikeampi ominaisuus.
Apulause 33.1 (Fii-funktion summa) Olkoon \(n\) positiivinen kokonaisluku. Jos summataan luvut \(\phi(d)\), missä \(d\) käy läpi luvun \(n\) tekijät, on lopputulos \(n\): \[\sum_{d \mid n} \phi(d) = n.\]
Siis esimerkiksi tapauksessa \(n = 12\) lause väittää, että \[\phi(1) + \phi(2) + \phi(3) + \phi(4) + \phi(6) + \phi(12) = 12.\] Tämä tapaus on helppo tarkistaa laskemalla.
Todistus. Kuinka monta on niitä kokonaislukuja \(x\), joilla \(1 \le x \le n\)? Vastaus on tietysti \(n\).
Määrän voi kuitenkin laskea toisellakin tavalla. Ideana on laskea kullekin positiiviselle kokonaisluvulle \(m\), monellako kokonaisluvulla \(x\) pätee \(1 \le x \le n\) ja \(\text{syt}(x, n) = m\). Kun summataan nämä määrät kaikilla \(m\), tulee vastaukseksi \(n\).
Montako näitä lukuja sitten on? Jos \(m\) ei jaa lukua \(n\), niin vastaus on tietysti nolla. Kysymys on siis kiinnostava vain jos \(m \mid n\). Tapauksessa \(m = 1\) määrä on määritelmän nojalla \(\phi(n)\). Käy niin, että määrä voidaan muissakin tapauksissa esittää fii-funktion avulla.
Jotta voi olla \(\text{syt}(x, n) = m\), tulee lukujen \(x\) ja \(n\) olla jaollisia luvulla \(m\). Kirjoitetaan siis \(x = my\) ja \(n = mk\). Nyt \[\text{syt}(x, n) = \text{syt}(my, mk) = m \cdot \text{syt}(y, k).\] Tulee siis päteä \(\text{syt}(y, k) = 1\).
Huomataan, että kun \(x\) käy läpi luvulla \(m\) jaolliset luvut välillä \(1 \le x \le n\), luku \(y\) käy läpi kaikki luvut välillä \(1 \le y \le n/m = k\). Täten niitä lukuja \(1 \le y \le k\), joilla \(\text{syt}(y, k) = 1\), on määritelmän nojalla \(\phi(k)\).
Eli ehdot \(1 \le x \le n, \text{syt}(x, n) = m\) toteuttavia \(x\) on \(\phi(n/m)\) (kun \(m \mid n\)), joten yhteensä lukuja \(1 \le x \le n\) on toisaalta \[\sum_{m \mid n} \phi(n/m)\] ja toisaalta \(n\). Enää pitää huomata, että kun \(m\) käy läpi luvun \(n\) tekijät, niin myös \(m/n\) käy läpi luvun \(n\) tekijät. Jos vaikka \(n = 12\) ja \(m\) käy tekijät läpi järjestyksessä \[1, 2, 3, 4, 6, 12,\] niin \(n/m\) käy tekijät läpi järjestyksessä \[12, 6, 4, 3, 2, 1.\] Täten \[\sum_{m \mid n} \phi(m) = n.\]
33.5 Primitiivijuuren olemassaolo
Pääsemme varsinaiseen todistukseen. Olkoon \(p\) alkuluku. Todistus pyörii seuraavan kysymyksen ympärillä.
Tiedämme, että jokaisen luvun aste modulo \(p\) jakaa luvun \(p-1\) (Tehtävän 6 osa (iii) Kertolasku kongruensseissa -tekstistä). Täten vastaus kysymykseen on \(0\), jos \(d\) ei jaa lukua \(p-1\).
Tutkitaan sitten kysymystä, kun \(d\) jakaa luvun \(p-1\). Jos \(d = p-1\), kysymys on sama kuin kysyisi montako primitiivijuurta on modulo \(p\). Kysymys voi siis aluksi tuntua vaikeammalta kuin tutkittava ongelma, mutta ongelma saadaan kuitenkin ratkaistua tätä kautta.
Väite. Vastaus kysymykseen on joko \(0\) tai \(\phi(d)\).
Väitteen perustelu. Jos ei ole olemassa yhtään sellaista lukua modulo \(p\), jonka aste on \(d\), niin vastaus on \(0\) ja väite pitää paikkaansa. Oletetaan siis, että modulo \(p\) on vähintään yksi luku \(a\), jonka aste on \(d\).
Tutkitaan lukuja \(a^1, a^2, \ldots , a^d\). Huomaa, että \(a^d \equiv 1 \pmod{p}\). Näitä lukuja voi visualisoida \(d\):n luvun rinkinä. Esimerkiksi alla olevassa kuvassa on visualisoitu tapaus \(d = 12\). Vertaa kuvaa kuvaan 1. (Huomaa, että emme ota kantaa siihen, onko tässä kaikki luvut modulo \(p\).)
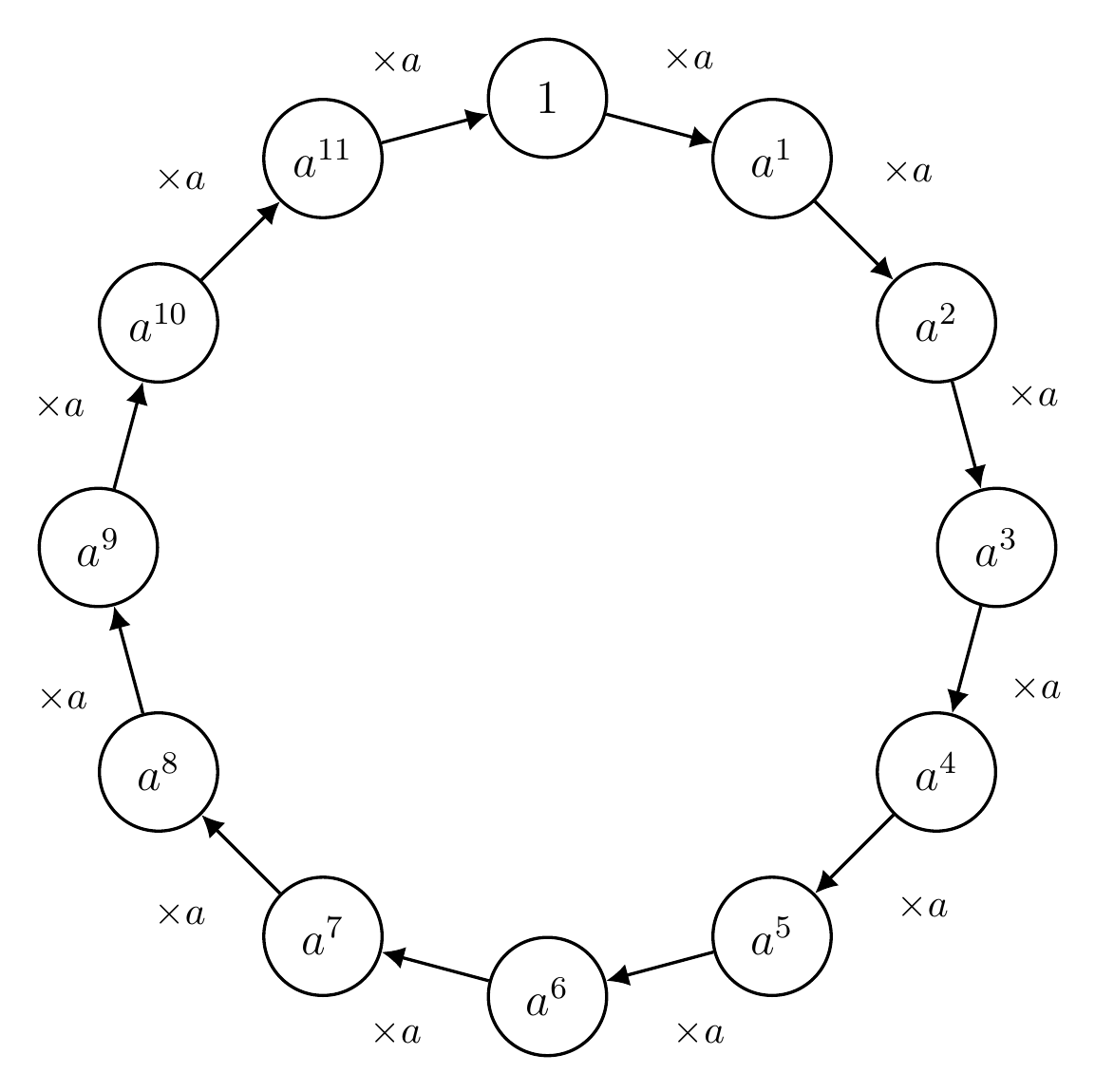
Luvuista \(a^1, a^2, \ldots , a^d\) tehdään seuraavat huomiot.
- Mikä tahansa näistä luvuista korotettuna potenssiin \(d\) on \(1 \pmod{p}\).
- Täten kukin luvuista \(a^1, a^2, \ldots , a^d\) on yhtälön \(x^d - 1 \equiv 0 \pmod{p}\) ratkaisu.
- Ne luvut, joiden aste on tasan \(d\), ovat muotoa \(a^x\), missä \(\text{syt}(x, d) = 1\). Näitä lukuja on \(\phi(d)\) kappaletta.
Kohdan (iii) nojalla vastaus kysymykseen on vähintään \(\phi(d)\). Voiko se olla suurempi? Ei: Jos on olemassa jokin luku \(b\), jonka aste on \(d\), on se yhtälön \(x^d - 1 \equiv 0 \pmod{p}\) ratkaisu. Kohdan (ii) nojalla olemme löytäneet tälle yhtälölle jo \(d\) ratkaisua. Lagrangen lauseen nojalla enempää ei ole, joten \(b\) on yksi luvuista \(a^1, a^2, \ldots , a^d\), joten se on otettu mukaan laskuihin kohdassa (iii).
Väite on näin ollen perusteltu.
Paranneltu väite. Vastaus kysymykseen on \(\phi(d)\) aina, kun \(d \mid p-1\).
Parannellun väitteen perustelu. Olkoon vastaus kysymykseen \(f(d)\). Väitteen nojalla \(f(d)\) on \(0\) tai \(\phi(d)\). Haluaisimme poissulkea vaihtoehdon \(f(d) = 0\) (kun \(d \mid p-1\)).
Mitä tiedämme luvuista \(f(d)\), kun \(d\) käy läpi luvun \(p-1\) tekijät? Oleellinen tieto on, että näiden lukujen summa on \(p-1\): jokaisen luvuista \(1, 2, \ldots , p-1\) aste on jokin luvun \(p-1\) tekijä.
Seuraavaan taulukkoon on kirjattu tämä tieto sekä muita tähän mennessä saatuja tietoja luvuista \(f(d)\). Taulukko on esimerkin vuoksi kirjoitettu tapaukselle \(p = 13\).

Tässä tapauksessa on selvää, että jokaisen luvuista \(f(d)\) tulee olla \(\phi(d)\): muutenhan oikean sarakkeen summa olisi pienempi kuin vasemman, mutta tiedämme molempien summien olevan \(p-1\).
Yleisessä tapauksessa menetellään vastaavasti. Osiossa 5 todistimme, että sarakkeen \(\phi(d)\) summa on \(p-1\), ja totesimme juuri, että sarakkeen \(f(d)\) summan tulee myös olla \(p-1\). Tästä seuraa, että jokaisen luvuista \(f(d)\) on oltava \(\phi(d)\).
Erityisesti \(f(p-1) = \phi(p-1) \ge 1\), eli on olemassa vähintään yksi primitiivijuuri modulo \(p\).
33.6 Tehtäviä
Ensimmäisissä tehtävissä tutustutaan tarkemmin fii-funktion ominaisuuksiin, ja viimeiset tehtävät ovat soveltavampia.
Tehtävä 1.
- Osoita, että jos \(p\) on alkuluku, niin \(\phi(p) = p-1\).
- Osoita, että jos \(p\) on alkuluku ja \(k\) on positiivinen kokonaisluku, niin \(\phi(p^k) = p^k - p^{k-1}\).
Tehtävä 2. Todista tehtävän 1 avulla, että jos \(n = p^k\) on jonkin alkuluvun potenssi, niin \[\sum_{d \mid n} \phi(d) = n.\]
Tehtävä 3. Tämän tehtävän tavoite on osoittaa, että jos \(\text{syt}(n, m) = 1\), niin \(\phi(nm) = \phi(n)\phi(m)\).
- Olkoon \(1 \le x \le mn\) kokonaisluku, ja olkoot \(1 \le y \le m\) ja \(1 \le z \le n\) luvun \(x\) jakojäännökset luvuilla \(m\) ja \(n\) jaettaessa. Osoita, että \(\text{syt}(x, mn) = 1\), jos ja vain jos \(\text{syt}(y, m) = 1\) ja \(\text{syt}(z, n) = 1\).
- Viimeistele todistus kiinalaisella jäännöslauseella.
Tehtävä 4. Laske \(\phi(360)\).
Tehtävä 5. Olkoon \(m > 1\) kokonaisluku, joka ei ole alkuluku. Osoita, että on olemassa polynomi \(P(x)\), jonka kertoimet ovat kokonaislukuja ja jonka kaikki kertoimet eivät ole jaollisia \(m\):llä ja jolla yhtälöllä \(P(x) \equiv 0 \pmod{m}\) on yli \(P\):n asteen verran ratkaisuja.
Tehtävä 6. Olkoon \(p\) alkuluku. Osoita, että \[1 \cdot 2 \cdot 3 \cdot \ldots \cdot (p-1) \equiv -1 \pmod{p}.\]
Tehtävä 7. Olkoon \(p\) alkuluku, jolla \(p \equiv 3 \pmod{4}\). Oletetaan, että \(x\) ja \(y\) ovat kokonaislukuja, joilla \(x^2 + y^2 \equiv 0 \pmod{p}\). Osoita, että \(x \equiv 0 \pmod{p}\) ja \(y \equiv 0 \pmod{p}\).
Tehtävä 8. (Eulerin lause) Olkoon \(m\) positiivinen kokonaisluku ja olkoon \(a\) kokonaisluku, jolla \(\text{syt}(a, m) = 1\). Osoita, että \(a^{\phi(m)} = 1 \pmod{m}\).