22  Konstruktiot

22.2 Esimerkkitehtäviä

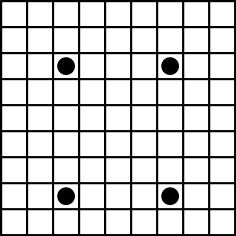
On houkuttelevaa ryhtyä suoraan hommiin ja yrittää saada tehtyä toimiva väritys. Tehtävä ei ole kuitenkaan aivan helppo, ja ihan vain satunnaisia kokeiluja tekemällä ratkaisu ei löydy. (Lukija voi toki yrittää!) Voi myös yrittää värittää niin pitkälle kuin pystyy ja umpikujaan joutuessa vaihtaa joidenkin ruutujen väriä ja yrittää uudestaan. Tämäkään ei toimi kovin helposti.

Pitää siis miettiä vähän. Miten väritys kannattaa tehdä? Varmaankin jokaista väriä kannattaa käyttää (suunnilleen) saman verran. Vaikuttaa hyvältä, jos jokaisella pysty- ja vaakarivillä on kutakin väriä kolme kappaletta. (Ongelmia tulee helposti, jos yhdellä rivillä on hyvin paljon samaa väriä.)

Lisäksi on järkevää yrittää pitää tilanne mahdollisimman symmetrisenä värien suhteen. Tällöin riittää miettiä vain yhtä väriä ja varmistaa, ettei se luo kiellettyä suorakulmiota.

Näillä ideoilla on luonteva värittää ruudukon kolme alinta riviä seuraavasti:

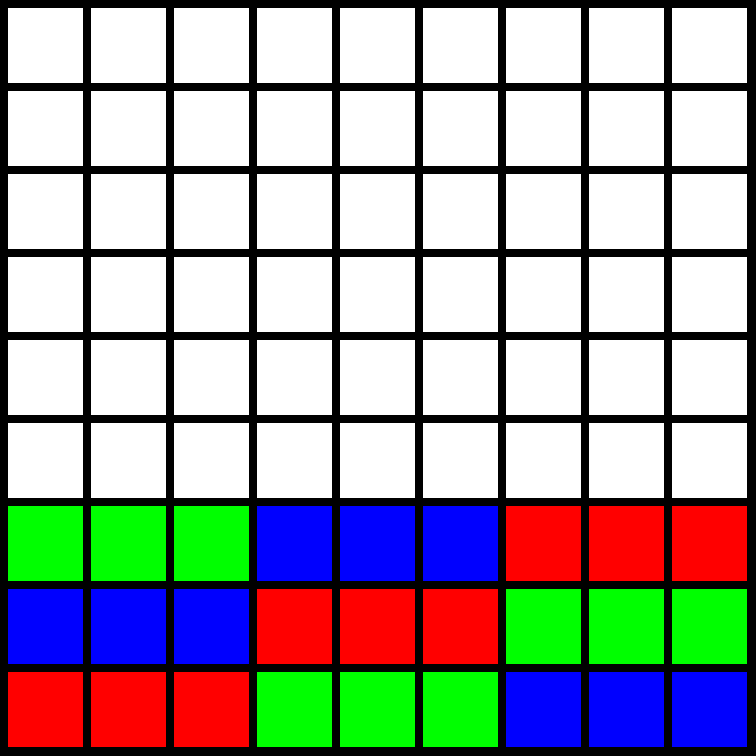
Huomataan, että tästä lähtien kunkin vaakarivin kolme punaista ruutua tulee laittaa niin, että yksi niistä on ruudukon vasemmassa, toinen keskimmäisessä ja kolmas oikeassa kolmanneksessa (ja vastaavasti myös siniselle ja vihreälle). Luonteva jatko on laittaa seuraavan vaakarivin punaiset ruudut jokaisen kolmanneksen ensimmäiseen ruutuun, seuraavalla vaakarivillä toiseen ruutuun ja sitä seuraavalla kolmansiin ruutuihin. Selkeyden vuoksi väritämme tästä eteenpäin vain punaiset ruudut: muut värit hoidetaan vastaavasti.

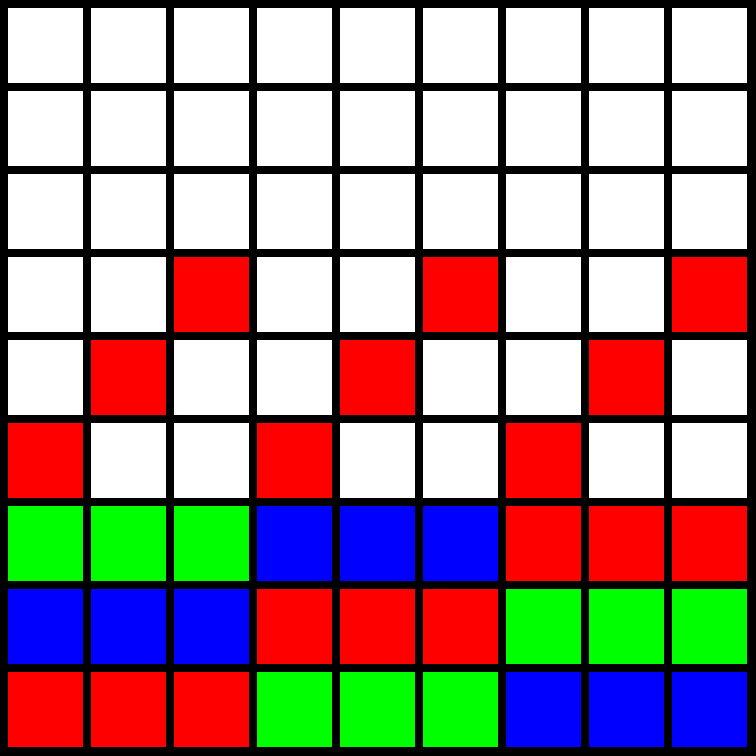
Ylimmille kolmelle vaakariville ei käytännössä ole vaihtoehtoja. Jos seuraavalla vaakarivillä yksi punainen ruutu on pystyrivillä \(1\), tulee kahden muun olla pystyriveillä \(5\) ja \(9\) tai \(6\) ja \(8\). Nämä vaihtoehdot ovat melko samanlaisia toisiinsa nähden, joten valitaan vaikkapa ensimmäinen.

Enää ei ole vaikea keksiä, miten kaksi muuta vaakariviä tulee värittää (vaihtoehtoja ei tosiaankaan ole montaa). Tässä ratkaisu.

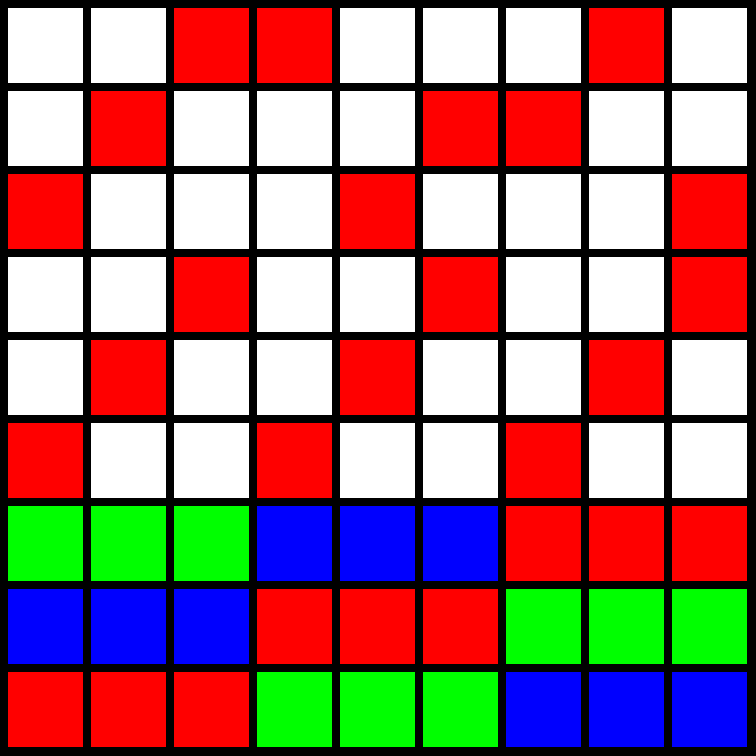
Ja kuten todettiin, muut värit hoidetaan samalla tavalla.

Huomataan, että jos (ii) pätee arvoilla \(n = 2\) ja \(n = 3\), niin se pätee kaikilla \(n\). Esimerkiksi arvolla \(n = 5\) väitteen saa tällöin siitä, että \(P(x)^5 = P(x)^2P(x)^3\) on tulo kahdesta polynomista, joiden kertoimet ovat positiivisia, joten myös tulon kertoimet ovat positiivisia.

Lähdetään sitten etsimään tällaista polynomia. Tutkitaan pieniä tapauksia. \(P(x)\) ei selvästikään voi olla vakiopolynomi.

Jos \(P\) on ensimmäisen asteen polynomi \(ax+b\), niin \[P(x)^2 = a^2x^2 + 2abx + b^2.\] Koska polynomin \(P(x)^2\) kertoimien pitää olla positiivisia ja termin \(x\) kerroin on \(2ab\), täytyy lukujen \(a\) ja \(b\) olla samanmerkkisiä. Jotta \(P(x)\):llä on negatiivinen kerroin, tulee molempien olla negatiivisia. Mutta nyt polynomin \(P(x)^3\) kertoimet ovat negatiivisia.

Ennen kuin edetään pidemmälle on hyvä huomata, että jos polynomin \(P(x)\) korkeimman asteen termin kerroin on \(s\) ja vakiotermi on \(t\), niin polynomin \(P(x)^3\) korkeimman asteen termin kerroin on \(s^3\) ja vakiotermi on \(t^3\). Täten näiden kertoimien tulee olla positiivisia.

Jos \(P(x)\) on toisen asteen polynomi \(P(x) = ax^2 + bx + c\), tulee edellisen nojalla lukujen \(a\) ja \(c\) olla positiivisia ja luvun \(b\) negatiivinen. Nyt kuitenkin nähdään, että polynomin \(P(x)^2\) termin \(x^3\) kerroin on \(2ab\) ja siten negatiivinen.

Jos \(P(x)\) on kolmannen asteen polynomi \(P(x) = ax^3 + bx^2 + cx + d\), niin taas lukujen \(a\) ja \(d\) tulee olla positiivisia. Jos \(b\) on negatiivinen, on polynomin \(P(x)^2\) termin \(x^5\) kerroin \(2ab\) ja siten negatiivinen. Jos \(c\) on negatiivinen, on polynomin \(P(x)^2\) termin \(x\) kerroin \(2cd\), mikä ei myöskään käy.

Vastaavalla idealla huomataan, että yleisesti polynomin \(P(x)\) toiseksi korkeimman asteen termin ja termin \(x\) kertoimien tulee olla positiivisia.

Entä jos \(P(x)\) on neljännen asteen polynomi \(ax^4 + bx^3 + cx^2 + dx + e\)? Näistä kertoimien \(a, b, d\) ja \(e\) kertoimien tulee olla positiivisia ja \(c\):n negatiivinen. Laskeminen alkaa mennä työlääksi. Huomataan kuitenkin, että tämä toimii, kunhan kertoimet valitsee sopivasti: esimerkiksi \[P(x) = x^4 + x^3 - \frac{1}{1000}x^2 + x + 1\] kelpaa. Miksi? Kun polynomia \(P(x) \cdot P(x)\) kerrotaan auki, aina, kun jonkin termin \(x^k\) kertoimeen tulee negatiivisuutta polynomin \(P(x)\) termin \(-x^2/1000\) takia, tulee sinne myös positiivisuutta joistain muista termeistä. Summasta tulee positiivinen, koska kerroin \(-1/1000\) on niin pieni. (Jos ei näe tätä muuten, voi tämän tarkistaa laskemalla.) Vastaavasti polynomin \(P(x)^3\) kertoimet ovat positiivisia.

Ratkaisun idea lyhyesti: Meillä on tolkuttomasti valinnanvaraa siinä, millaisen jonon luomme. Annettu ehto puolestaan ei ole kovin rajoittava. Rohkeasti ”tekemällä vaan” saadaan luotua halutunlainen jono.

Itse ratkaisuun. Muodostetaan jonolle alku vaikka seuraavasti: \[x_1 = 1, x_2 = 10, x_3 = 100, x_4 = 1000.\] Lisätään sitten jonoon yksitellen lisää alkioita. Haluamme taata seuraavat kaksi asiaa:

1. Mitään lukua ei voida esittää yli yhdellä tavalla jonon alkioiden erotuksena.
2. Jokainen luku voidaan esittää jonon alkioiden erotuksena.

Nämä ehdot saadaan toteutettua lisäämällä jonoon seuraavalla logiikalla lisää lukuja:

Olkoon \(m\) pienin positiivinen kokonaisluku, joka ei toistaiseksi ole minkään kahden jonon alkion erotus ja olkoon \(M\) suurin luku, joka toistaiseksi esiintyy jonossa. Lisätään jonon perään hyvin iso luku, esimerkiksi \(1000M\), ja sitten \(1000M + m\).

Ajatus on, että nyt luku \(m\) voidaan esittää kahden jonon alkion erotuksena: \((1000M + m) - 1000M = m\). Uudet luvut valittiin suuriksi sillä ajatuksella, ettei mitään muuta lukua voida esittää yli yhdellä tavalla jonon lukujen erotuksena. Tarkistetaan tämä.

Jos jonossa oli aiemmin luvut \(x_1, x_2, \ldots , x_n\), niin uudet erotukset ovat \[1000M - x_1, 1000M - x_2, \ldots , 1000M - x_n\] ja \[1000M + m - x_1, 1000M + m - x_2, \ldots , 1000M + m - x_n\] sekä aiemmin mainittu \((1000M + m) - 1000M = m\).

Ensin huomataan, että mikä tahansa uusista erotuksista on suurempi kuin vanhat erotukset \(x_i - x_j\) sekä \(m\) (poislukien erotus \(m\)), koska \(M\) on niin suuri. Riittää siis tarkistaa, ettei uusien erotusten joukossa ole kahta samaa. Selvästikään mitkään kaksi ensimmäisen rivin lukua eivät ole samoja, kuten eivät myöskään mitkään kaksi toisen rivin lukua. Myöskään \[1000M - x_i = 1000M + m - x_j\] ei ole mahdollista, koska tästä seuraisi \[x_j - x_i = m,\] mutta oletimme, että lukua \(m\) ei voi esittää erotuksena tällä tavalla.

Toistamalla yllä esitettyä prosessia saadaan yksitellen varmistettua, että jokainen positiivinen kokonaisluku \(m\) on kahden jonon luvun erotus varmistaen samalla, ettei mikään luku ole useammalla tavalla jonon lukujen erotus.