31 Lineaariset rekursiot

Tekijä

Olli Järviniemi

31.1 Johdanto

Varsin tunnettu Fibonaccin lukujono koostuu luvuista \[1, 1, 2, 3, 5, 8, 13, 21, 34, \ldots\] Jono alkaa kahdella kappaleella lukua \(1\) ja sen seuraava luku on aina kahden edellisen summa. Lukujono saadaan siis määrittelemällä \(F_1 = 1, F_2 = 1\) ja \[F_{n+2} = F_{n+1} + F_n\] kaikilla \(n = 1, 2, 3, \ldots\)

Tilannetta voi yleistää tutkimalla lukujonoja, joissa seuraava jäsen saadaan ottamalla muutama edellinen termi, kertomalla niitä joillain vakioilla ja summaamalla lopputulokset. Tällaisia lukujonoja kutsutaan lineaarisesti rekursiivisiksi. Esimerkiksi ehdoilla \(a_0 = 0, a_1 = 1, a_2 = 4\) ja \[a_{n+3} = 3a_{n+2} - 3a_{n+1} + a_n, \quad \text{kun } n = 0, 1, 2, \ldots\] määritelty lukujono on lineaarisesti rekursiivinen. (Harjoitus lukijalle: mikä lukujono on kyseessä?)

Tässä tekstissä käsitellään lineaarisesti rekursiivisia lukujonoja. Ensin esitetään yleinen menetelmä lukujonon kaavan ratkaisemiseksi. Tämän jälkeen käydään läpi esimerkkitehtäviä.

31.2 Lukujonon kaava

Ehkä hieman yllättäen mille tahansa lineaarisesti rekursiiviselle lukujonolle voidaan löytää kaava. Esitetään menetelmä esimerkin kautta.

Tehtävä 31.1 Määritellään \(a_1 = 1, a_2 = 5\) ja \[a_{n+2} = 5a_{n+1} - 6a_n\] kaikilla \(n = 1, 2, 3, \ldots\) Määritä kaava lukujonon jäsenille.

Lasketaan hieman ensimmäisiä arvoja, jos säännönmukaisuus sattuisi löytymään.

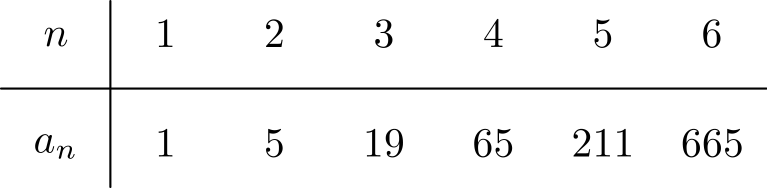
Selvää logiikkaa ei löydy, mutta yksi asia on selvä: lukujono kasvaa hyvin nopeasti. Tarkemmin katsottuna seuraava jäsen on suunnilleen kolminkertainen edelliseen nähden, eli kasvu vaikuttaa eksponentiaaliselta.

Tästä motivoituneena tehdään arvaus.

Arvaus 1. Arvataan, että \(a_n = c^n\) jollakin vakiolla \(c\).

Toimiiko tämä? Jotta pätee \(a_{n+2} = 5a_{n+1} - 6a_n\), tulee olla \[c^{n+2} = 5c^{n+1} - 6c^n.\] Tietysti \(c = 0\) toteuttaa yhtälön, mutta tämä ei ole kiinnostavaa. Oletetaan, että \(c \neq 0\). Jakamalla puolittain luvulla \(c^n\) saadaan \[c^2 = 5c - 6.\] Tämä on toisen asteen yhtälö, jolla on ratkaisut \(c = 2\) ja \(c = 3\).

Selvästikään kumpikaan arvauksista \(a_n = 2^n\) ja \(a_n = 3^n\) ei ole oikein: kummallakaan ei päde \(a_1 = 1\). Arvausta pitää parantaa.

Arvaus 2. Arvataan, että \(a_n = k \cdot c^n\), missä \(k\) on jokin vakio ja \(c = 2\) tai \(c = 3\).

Huomataan, että tämä toteuttaa edelleen rekursioyhtälön: yhtälö \[kc^{n+2} = 5kc^{n+1} - 6kc^n\] selvästi pätee jos \(k = 0\), ja jos \(k\) ei ole nolla, voidaan jakaa puolittain luvulla \(kc^n\) ja saada yhtälö \[c^2 = 5c - 6.\] Tämä on sama yhtälö kuin aiemminkin, eli \(c = 2\) ja \(c = 3\) ovat taas ratkaisuja.

Ikävä kyllä tämäkään arvaus ei vielä toimi. Tapauksessa \(c = 2\) jonon \(a_n = kc^n\) ensimmäiset arvot ovat \(a_1 = 2k\) ja \(a_2 = 4k\), ja haluamme niiden olevan \(a_1 = 1\) ja \(a_2 = 5\). Kuitenkaan ei voi samanaikaisesti päteä sekä \(2k = 1\) että \(4k = 5\). Vastaavasti tapauksessa \(c = 3\) tulisi päteä \(3k = 1\) ja \(9k = 5\), mikä ei onnistu.

Arvaukseen tarvitaan vielä yksi parannus.

Arvaus 3. Arvataan, että \(a_n = x \cdot 2^n + y \cdot 3^n\), missä \(x\) ja \(y\) ovat joitain vakioita.

Huomataan, että tämäkin arvaus toteuttaa rekursioyhtälön. Arvauksen 2 kohdalla nimittäin huomattiin, että \[x \cdot 2^{n+2} = 5x \cdot 2^{n+1} - 6x \cdot 2^n\] ja \[y \cdot 3^{n+2} = 5y \cdot 3^{n+1} - 6y \cdot 3^n.\] Summaamalla nämä yhtälöt saadaan

\[x \cdot 2^{n+2} + y \cdot 3^{n+2} = 5x \cdot 2^{n+1} + 5y \cdot 3^{n+1} - (6x \cdot 2^n + 6y \cdot 3^n).\]

Tämä on juuri mitä haluamme: tämä kertoo, että arvauksemme \(a_n = x \cdot 2^n + y \cdot 3^n\) toteuttaa yhtälön \[a_{n+2} = 5a_{n+1} - 6a_n.\]

Entä alkuarvot? Jotta pätee \(a_1 = 1\), tulee päteä \(x \cdot 2^1 + y \cdot 3^1 = 1\) eli \[2x + 3y = 1.\] Jotta pätee \(a_2 = 5\), tulee vastaavasti päteä \(x \cdot 2^2 + y \cdot 3^2 = 5\) eli \[4x + 9y = 5.\] Tämä on yhtälöpari, jonka ratkaisuksi saadaan \(x = -1\), \(y = 1\).

Täten \[a_n = 3^n - 2^n\] toteuttaa rekursioyhtälön ja alkuarvot menevät oikein, eli tämä antaa oikean tuloksen kaikilla \(n\). Lauseke \(3^n - 2^n\) on hyvinkin siisti kaava lukujonolle.

Kommentti. Sama menetelmä toimii yleisemminkin. Fibonaccin lukujonon tapauksessa arvauksessa 1 saadaan toimiviksi \(c\):n arvoiksi yhtälön \[c^2 = c + 1\] ratkaisut. Tämän yhtälön ratkaisut eivät ole kokonaislukuja vaan melko ikävän näköisiä: \[c_1 = \frac{1 + \sqrt{5}}{2}, \quad c_2 = \frac{1 - \sqrt{5}}{2}.\] Tämän jälkeen edetään kuten yllä, eli vastaus on muotoa \(a_n = xc_1^n + yc_2^n\). Lukujen \(x\) ja \(y\) arvot voidaan ratkaista kuten edellä alkuarvojen antaman yhtälöparin kautta, mutta nekin ovat melko ikävän näköisiä. Laskuja ei esitetä tässä, mutta lopulta kuitenkin saadaan, että \[F_n = \frac{1}{\sqrt{5}}\left(\frac{1 + \sqrt{5}}{2}\right)^n - \frac{1}{\sqrt{5}}\left(\frac{1 - \sqrt{5}}{2}\right)^n.\]

Yleisesti ongelmassa pitää ratkaista vastaava polynomiyhtälö. Joissakin tapauksissa yhtälöllä on moninkertaisia nollakohtia. Esimerkiksi johdannon esimerkissä \[a_{n+3} = 3a_{n+2} - 3a_{n+1} + a_n\] yhtälöksi tulee \(c^3 = 3c^2 - 3c + 1\) eli \((c-1)^3 = 0\). Moninkertaisen nollakohdan tapauksessa eksponentiaalisia arvauksia pitää lisäksi kertoa polynomeilla. Tässä tapauksessa arvaukset ovat \(1^n, n \cdot 1^n\) ja \(n^2 \cdot 1^n\). On helppo tarkistaa, että nämä toteuttavat rekursioyhtälön.¹

Yleisessä tapauksessa lineaarisen rekursioyhtälön ratkaisut ovat siis summia termeistä muotoa ”polynomi kertaa eksponenttifunktio”. (Tämän väitteen todistaminen on melko vaikeaa, joten sitä ei tehdä tässä.)

¹ Yleisesti kaksinkertaisen nollakohdan \(c\) tapauksessa myös arvaus \(nc^n\) toimii. Jos \(c\) on kolminkertainen nollakohta, niin myös \(n^2c^n\) toimii, ja niin edelleen.

31.3 Esimerkkitehtäviä

Yksi sovelluskohde (lineaarisille) rekursioille ovat kombinatoriset ongelmat. Tekstissä Induktiivinen päättely nähtiinkin yksi sovellus liittyen merkkijonoihin, joissa ei ole kahta \(a\)-kirjainta peräkkäin.

Tässä annetaan pari algebrallisempaa esimerkkiä.

Tehtävä 31.2 Lukujonon \(a_1, a_2, \ldots\) kaikki jäsenet ovat kokonaislukuja ja on olemassa reaaliluvut \(x\) ja \(y\), joilla \[a_{n+2} = xa_{n+1} + ya_n\] kaikilla \(n \ge 1\). Lisäksi tiedetään, että jono \(a_1, a_2, \ldots\) ei ole vakiojono. Ovatko \(x\) ja \(y\) välttämättä kokonaislukuja?

Vastaus: Ei, lukujen \(x\) ja \(y\) ei tarvitse olla edes rationaalisia!

Valitaan jokin yksinkertainen lukujono, joka on lineaarisesti rekursiivinen. Esimerkiksi \(a_n = 2^n\) käy hyvin. Nyt \(a_1, a_2, \ldots\) selvästikin toteuttaa lineaarisen rekursioyhtälön \[a_{n+1} = 2a_n,\] jota vastaava polynomiyhtälö on \(c-2 = 0\). Tämä lukujono toteuttaa kuitenkin myös monimutkaisempia rekursioyhtälöitä, kunhan niitä vastaavien polynomien nollakohdista löytyy \(2\). Esimerkiksi polynomiyhtälöä \((c-2)(c - \pi) = 0\) vastaa rekursioyhtälö \[a_{n+2} = (2 + \pi)a_{n+1} - 2\pi a_n,\] ja lukujono \(a_n = 2^n\) toteuttaa tämänkin yhtälön. Eli yksi vastaesimerkki tehtävään on \(x = 2 + \pi, y = 2\pi\) ja \(a_n = 2^n\).

Kommentti. Polynomeja käsittelevissä teksteissä on puhuttu siitä, kuinka polynomeja voi miettiä niiden kertoimien tai nollakohtien kautta. Lineaaristen rekursioiden tapauksessa tilanne on samankaltainen: suoraan rekursioyhtälön tuijottaminen ja siitä jonon jäsenien laskeminen vastaa polynomin miettimistä kertoimien kautta ja lukujonoa vastaavan polynomiyhtälön ja kaavan miettiminen vastaa polynomin miettimistä nollakohtien kautta. Tämä tehtävä on esimerkki tilanteesta, jossa jälkimmäinen ajattelutapa on parempi.

Tehtävä 31.3 Määritellään Fibonaccin lukujono asettamalla \(F_1 = F_2 = 1\) ja \(F_{n+2} = F_{n+1} + F_n\) kaikilla \(n \ge 1\). Olkoot \(n\) ja \(m\) sellaisia positiivisia kokonaislukuja, joilla \(m \mid n\). Osoita, että \(F_m \mid F_n\).

Tässä on taulukoitu vähän useampi Fibonaccin luku.

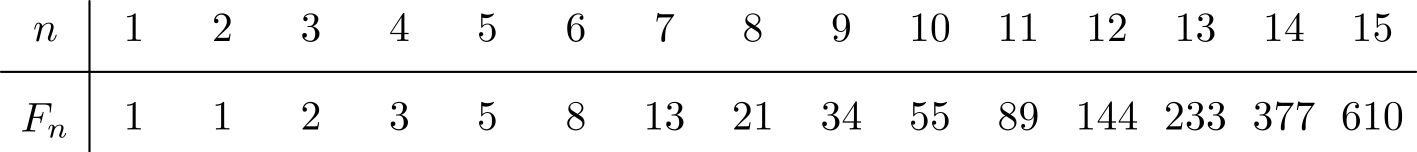
Tutkitaan aluksi jotakin helppoa tapausta, kuten \(n = 2m\). Tulee osoittaa, että \(F_m \mid F_{2m}\). Tapauksissa \(m = 6\) ja \(m = 7\) huomataan, että \[\frac{F_{12}}{F_6} = \frac{144}{8} = 18 = 5 + 13\] ja \[\frac{F_{14}}{F_7} = \frac{377}{13} = 29 = 8 + 21,\] mikä vihjaa siihen, että \[F_{2m} = F_m(F_{m-1} + F_{m+1}).\] (Tämä pätee myös pienemmillä \(m\):n arvoilla.)

Miten tällaisen identiteetin voisi todistaa? Yksi suoraviivainen tapa on kirjoittaa \[F_n = \frac{1}{\sqrt{5}}(a^n - b^n),\] missä \(a = (1 + \sqrt{5})/2\) ja \(b = (1 - \sqrt{5})/2\) ja sievennellä lausekkeita. Sieventämisessä käytetään apuna tietoja \(a^2 = a+1, b^2 = b+1\) ja Vietan kaavoista (Alaluku 12.3.2) (tai suoraan laskemalla) saatavia tietoja \(ab = -1, a+b = 1\).

Huomataan, että kahden neliön erotuksena \[\begin{align*} F_{2m} &= \frac{1}{\sqrt{5}}(a^{2m} - b^{2m}) \\ &= \frac{1}{\sqrt{5}}(a^m - b^m)(a^m + b^m) \\ &= F_m(a^m + b^m). \end{align*}\] Enää riittää perustella, miksi \(a^m + b^m = F_{m-1} + F_{m+1}\). Oikeastaan alkuperäistä tehtävää varten riittää perustella vain, että \(a^m + b^m\) on kokonaisluku. Tämä on hieman helpompaa, joten teemme vain tämän.

Idea on, että \(ab\) ja \(a+b\) ovat kokonaislukuja, ja näistä luvuista voidaan rakentaa muita lausekkeita luvuista \(a\) ja \(b\). Esimerkiksi yhtälössä \[(a+b)^2 = a^2 + 2ab + b^2\] termit \((a+b)^2\) ja \(2ab\) ovat kokonaislukuja, joten nyt myös \(a^2 + b^2\) on kokonaisluku. Yleisesti voimme todistaa induktiolla, että \(a^m + b^m\) on kokonaisluku. Riittää huomata, että summa \(a^m + b^m\) saadaan muodostettua lukujen \(a+b\) ja \(a^{m-1} + b^{m-1}\) tulon kautta: \[(a+b)(a^{m-1} + b^{m-1}) = a^m + b^m + (ab)(a^{m-2} + b^{m-2}).\] Nyt jos \(a^{m-1} + b^{m-1}\) ja \(a^{m-2} + b^{m-2}\) ovat kokonaislukuja, niin myös \(a^m + b^m\) on.

Olemme siis todistaneet, että \(F_m \mid F_{2m}\). Tehtävän todistamiseksi tarvitaan yleisemmin, että \(F_m \mid F_{km}\) kaikilla \(k \ge 1\). Tämän todistaminen onnistuu vastaavalla tavalla kuin yllä tapauksessa \(k = 2\): tekijöihinjaolla \(x^k - y^k = (x-y)(\cdots)\) saadaan

\[\begin{align*} F_{km} &= \frac{1}{\sqrt{5}}\left(a^{km} - b^{km}\right) \\ &=\frac{1}{\sqrt{5}}(a^m - b^m)\left((a^m)^{k-1} + (a^m)^{k-2}(b^m) + \ldots + (a^m)(b^m)^{k-2} + (b^m)^{k-1}\right) \\ &=F_m\left(a^{m(k-1)} + (ab)^ma^{m(k-3)} + \ldots + (ab)^mb^{m(k-3)} + b^{m(k-1)}\right). \end{align*}\]

Sulkulausekkeen termit voi ryhmitellä pareiksi, joiden summa on muotoa \[(ab)^{mi}(a^{mj} + b^{mj}).\] Tässä \(ab = -1\) on kokonaisluku ja edellä on todistettu, että \(a^n + b^n\) on aina kokonaisluku. Väite seuraa.

Kommentti. Tehtävän voi ratkaista myös lukuteoreettisesti. Fibonaccin luvut ovat jaksollisia modulo \(F_m\), ja jonon arvot modulo \(F_m\) ovat järjestyksessä (kun luvut kirjoitetaan sopivalla tavalla) \[\begin{multline*} F_1, F_2, \ldots , F_{m-2}, F_{m-1}, 0, \\ F_{m-1}, -F_{m-2}, F_{m-3}, -F_{m-4}, \ldots , \pm F_1, \mp F_1, 0, \\ \mp F_1, \mp F_1, \ldots, \end{multline*}\] eli arvot ovat melko säännöllisiä modulo \(F_m\). (Esimerkiksi modulo \(13 = F_7\) luvut ovat \(1, 1, 2, 3, 5, 8, 0, 8, -5, 3, -2, 1, -1, 0, -1, -1, \ldots\)) Tätä kautta nähdään, että jos \(n\) on jaollinen \(m\):llä, niin \(F_n \equiv 0 \pmod{F_m}\) eli \(F_m \mid F_n\).

Tätä kautta voidaan todistaa myös vahvempi väite \(\text{syt}(F_m, F_n) = F_{\text{syt}(m, n)}\).

31.4 Tehtäviä

Tehtävä 1. Olkoon \(a_n = n2^n\) kaikilla \(n \ge 1\). Etsi (lineaarinen) rekursioyhtälö, jonka lukujono \(a_1, a_2, \ldots\) toteuttaa.

Tehtävä 2. Lukujonolla \(a_1, a_2, \ldots\) pätee \(a_1 = 1, a_2 = 2\) ja \[a_{n+2} = 5a_{n+1} - 6a_n + n\] kaikilla \(n \ge 1\). Etsi suljettu muoto jonon termeille.

Tehtävä 3. Luvut \(x\) ja \(y\) ovat sellaisia, että luvut \(x+y, x^2+y^2, x^3+y^3\) ja \(x^4+y^4\) ovat kokonaislukuja. Osoita, että \(x^n + y^n\) on kokonaisluku kaikilla positiivisilla kokonaisluvuilla \(n\).

Tehtävä 4. Lukujonolla \(a_1, a_2, a_3, \ldots\) pätee \(a_1 = 4, a_2 = 9, a_3 = 25\) ja \[a_{n+3} = 7a_{n+2} - 14a_{n+1} + 8a_n\] kaikilla \(n \ge 1\). Osoita, että \(a_n\) on jonkin kokonaisluvun neliö kaikilla \(n = 1, 2, 3, \ldots\)

Tehtävä 5. Osoita, että on olemassa Fibonaccin luku, joka on jaollinen sadalla.