32 Inversio
32.1 Johdanto
Edellisessä geometrian tekstissä ja sen tehtävissä käsiteltiin muutamaa geometrista transformaatiota: peilauksia, skaalauksia, kiertoja ja siirtoja. Yksi tärkeä transformaatio kuitenkin puuttui: inversio. Tässä tekstissä esitellään inversio, käydään läpi sen perusominaisuudet ja annetaan pari esimerkkisovellusta kilpailutehtäviin.
Inversio on tähän mennessä käsitellyistä geometrian menetelmistä selvästi vaikein. Tästä syystä tämä teksti on tavallista pidempi. Etene rauhassa haukaten pieni pala kerrallaan.
32.2 Inversio
Peilauksessa valitaan suora tai piste, jonka yli peilataan. Skaalauksessa valitaan piste ja skaalauskerroin. Inversiossa puolestaan valitaan ympyrä.
Inversio \(O\)-keskisen, \(r\)-säteisen ympyrän suhteen määritellään seuraavasti: piste \(P\) kuvataan sellaiseksi pisteeksi \(P'\), joka on puolisuoralla \(OP\) ja jolla \(OP \cdot OP' = r^2\). Alla on muutama piste ja niiden kuvaukset, kun tehdään inversio kuvan ympyrän suhteen.
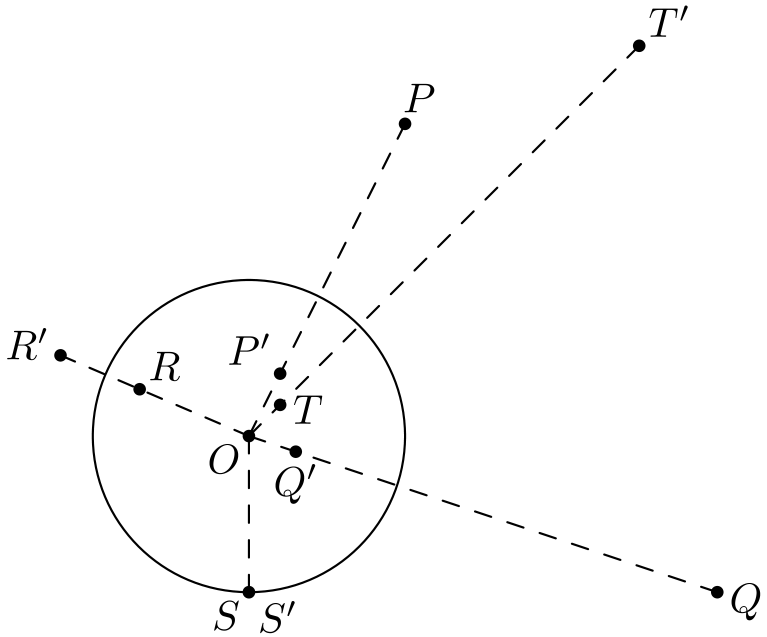
Erityisesti todetaan, että pistettä \(O\) lähellä olevat pisteet, kuten \(T\), kuvautuvat kauas. Vastaavasti kaukana olevat pisteet, kuten \(P\) ja \(Q\), kuvautuvat lähelle. Piste \(R\) on tältä väliltä ja sen kuvaus \(R'\) ei myöskään ole kovin kaukana tai lähellä pistettä \(O\). Ympyrällä oleva piste \(S\) on juuri sillä etäisyydellä, että sen kuvaus \(S'\) on yhtä kaukana pisteestä \(O\) kuin piste \(S\), eli \(S'\) ja \(S\) ovat sama piste.
32.3 Inversion ominaisuuksia
Alla listataan inversion tärkeimmät ominaisuudet. Näitä on paljon (seitsemän kappaletta). Listan sisältöä avataan todistuksessa kuvien avulla.
Tiivistäen: suorat ja ympyrät kuvautuvat joko suoriksi tai ympyröiksi riippuen siitä, kulkevatko ne pisteen \(O\) kautta vai eivät. Voi auttaa ajatella, että suora on vain ympyrä, jolla on äärettömän suuri säde, jolloin lauseen pääpointti (kohdat (iii), (v), (vi), (vii)) voidaan tiivistää muotoon ”ympyrät kuvautuvat ympyröiksi”.
Otetaan todistus askel kerrallaan.
Kohta (i). Valitaan jokin piste \(P\) ja tutkitaan, mitä tapahtuu, kun tehdään inversio kahdesti peräkkäin.
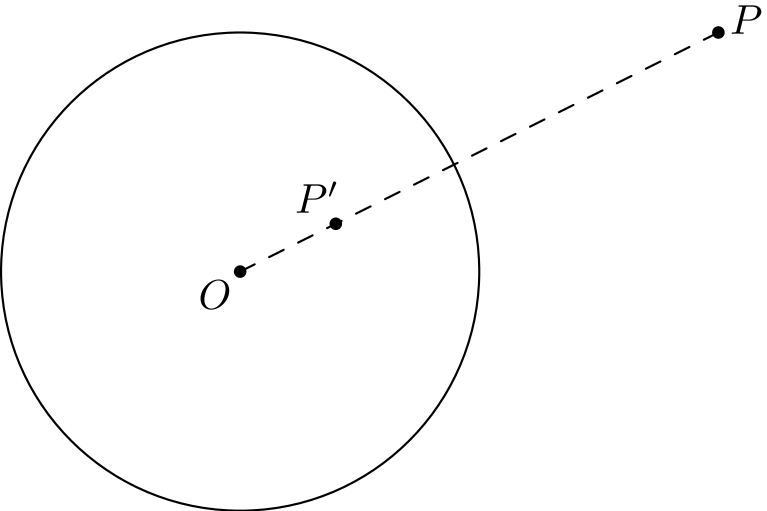
Pisteen \(P\) kuva inversion jälkeen on se piste \(P'\), jolla \(OP \cdot OP' = r^2\). Kun inversio tehdään uudestaan, kuvautuu piste \(P'\) sellaiseksi pisteeksi \(P''\), jolla \(OP' \cdot OP'' = r^2\). Näistä kahdesta yhtälöstä saadaan \(OP = OP''\), eli \(P\) ja \(P''\) ovat samalla etäisyydellä pisteestä \(O\). Toisaalta ne ovat molemmat puolisuoralla \(OP'\), joten ne ovat sama piste.
Kohta (ii). (Vertaa kuvan 32.1 pisteeseen \(S\).) Jos \(P\) on piste ympyrän kehällä ja \(P'\) on pisteen \(P\) kuvaus inversion jälkeen, niin pätee \(OP = r\) ja \(OP \cdot OP' = r^2\). Täten \(OP' = r\), mistä seuraa \(P = P'\).
Kohta (iii).
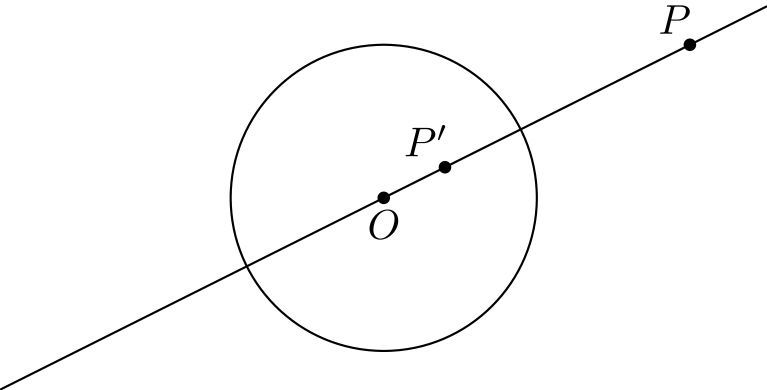
Inversion määritelmän perusteella jokainen suoran piste \(P\) kuvautuu suoralle johonkin pisteeseen \(P'\). Kohdan (i) nojalla piste \(P'\) kuvautuu inversiossa pisteeksi \(P\). Siis pisteet \(P\) ja \(P'\) vain vaihtavat paikkaa.
Kohta (iv). Tämä väite alkaa jo olla vaikeampi. Ideana on, että tilanne muistuttaa vahvasti pisteen potenssia. Käytämmekin pisteen potenssia toiseen suuntaan.
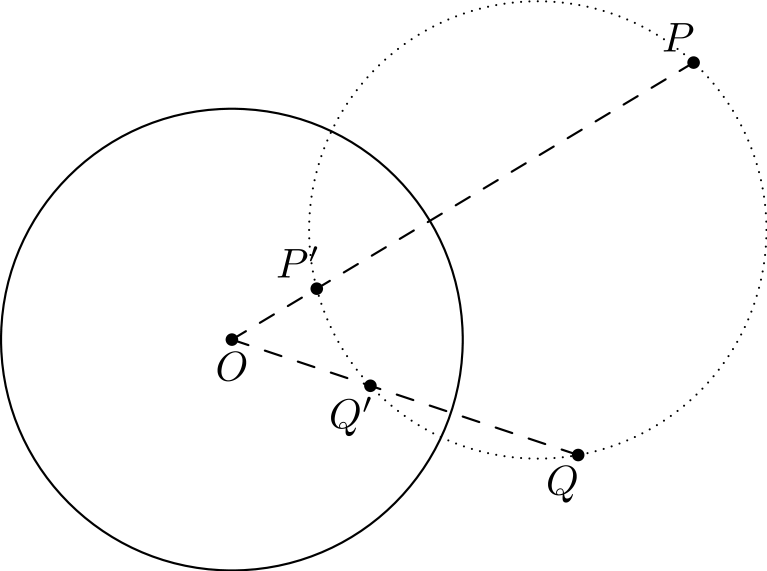
Kolmiot \(OPQ'\) ja \(OQP'\) ovat yhdenmuotoisia (sks), koska niillä on yhteinen kulma kärjessä \(O\) ja \[\frac{OP}{OQ'} = \frac{\frac{r^2}{OP'}}{\frac{r^2}{OQ}} = \frac{OQ}{OP'}.\] Täten \(\angle OPQ' = \angle P'QO\), eli pisteet ovat samalla ympyrällä.
Kohta (v). Tämäkään väite ei ole itsestäänselvä. Tilanne on esitetty seuraavassa kuvassa.
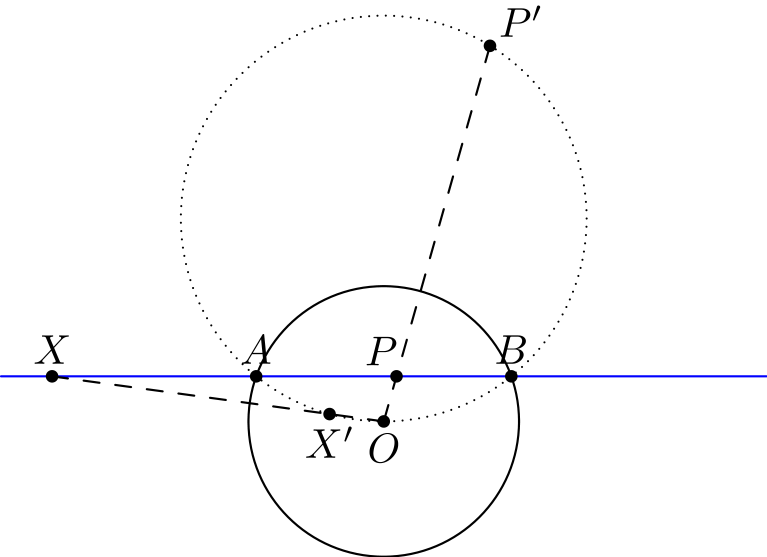
Tutkitaan hieman kuvaa ennen todistusta. Huomataan ensinnäkin, että kuvan tapauksessa sininen suora leikkaa \(O\)-keskisen ympyrän kahdessa pisteessä \(A\) ja \(B\). Nämä pysyvät inversion seurauksena paikoillaan (kohta (ii)). Siis jos inversion seurauksena suorasta todella tulee pisteen \(O\) kautta kulkeva ympyrä, niin kyseinen ympyrä on kolmion \(OAB\) ympärysympyrä.
On myös havainnollistavaa miettiä, mitä tapahtuu suoran niille pisteille, jotka ovat todella kaukana pisteestä \(O\). Kuvassa yksi tällainen piste on \(X\). Tämä piste kuvautuu hyvin lähelle pistettä \(O\) (kuvan piste \(X'\)). Siis sinisen suoran kaukana olevat pisteet kuvautuvat punaisen ympyrän pistettä \(O\) lähellä oleviksi pisteiksi. Vastaavasti sinisen suoran \(O\):ta lähellä olevat pisteet (kuten kuvan piste \(P\)) vastaavat punaisen ympyrän kaukana olevia pisteitä (piste \(P'\)).
Annetaan sitten väitteelle todistus. Todistus pyörii seuraavan kuvan ympärillä.
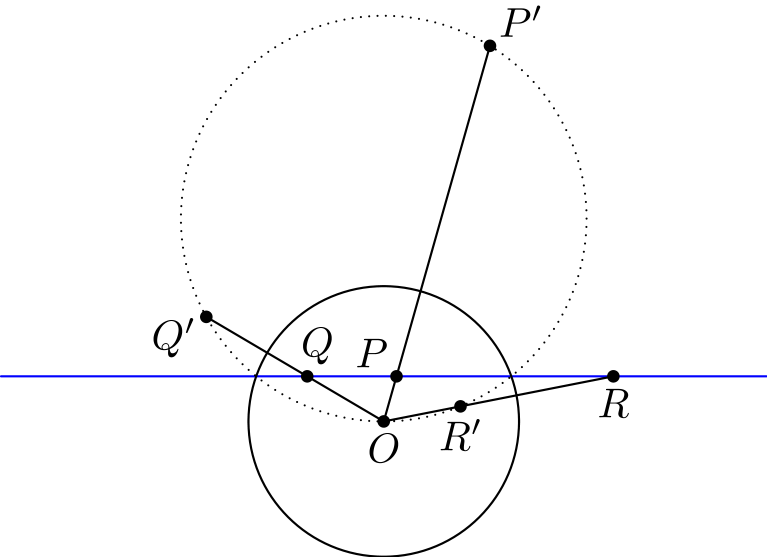
Olkoot \(P, Q\) ja \(R\) jotkin suoran pisteet, ja olkoot niiden kuvat inversion jälkeen \(P', Q'\) ja \(R'\). Todistetaan, että \(O, P', Q'\) ja \(R'\) ovat samalla ympyrällä. Ideana on jahdata kulmia käyttäen kohdan (iv) tulosta. Kulmanjahtaus on helppoa, koska jännenelikulmioita on niin monta.
Kohdan (iv) tulos sanoo nimittäin, että nelikulmiot
\[PP'Q'Q, \quad PP'RR' \quad \text{ja} \quad QQ'RR'\]
ovat jännenelikulmioita. Tämä tieto ja se, että pisteet \(P, Q\) ja \(R\) ovat samalla suoralla, antavat
\[\angle OQ'P' = 180^{\circ} - \angle P'PQ = \angle RPP' = \angle RR'P' = 180^{\circ} - \angle P'R'O,\]
mikä on haluttu väite.
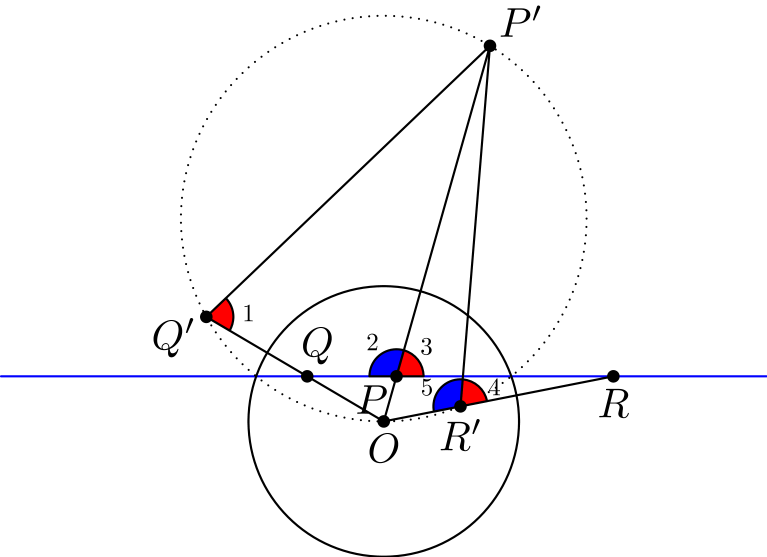
Kohta (vi). Samanlainen todistus kuin kohdassa (v) toimii. Tämä käy järkeen: jos tiedämme, että suora kuvautuu ympyräksi, niin kohdan (i) nojalla ympyrä kuvautuu suoraksi.
Kohta (vii). Viimeinen rutistus. Esimerkki kohdan tilanteesta on esitetty seuraavassa kuvassa.
Todistetaan väite. Todistusta varten valitaan sinisen ympyrän se halkaisija \(AB\), jolla \(O, A\) ja \(B\) ovat samalla suoralla, sekä jokin ympyrän piste \(C\). Tavoite on osoittaa, että \(C'\) on ympyrällä, jonka halkaisija on \(A'B'\).
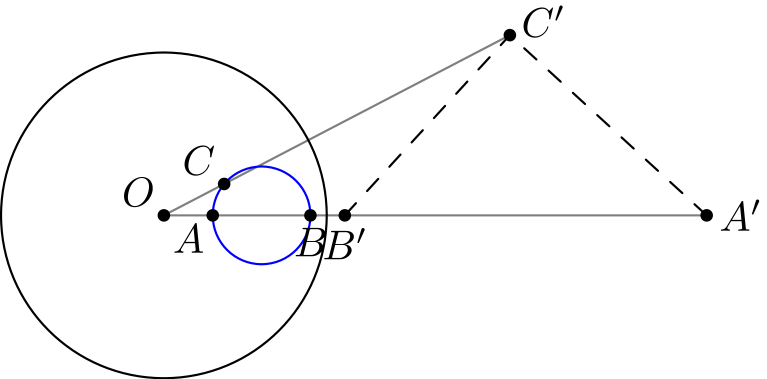
Käytämme taas kohdan (iv) tulosta jännenelikulmioiden saamiseksi. Tässä kuviossa \[AA'C'C \quad \text{ja} \quad BB'C'C\] ovat jännenelikulmioita. Loppu on kulmanjahtausta: käyttämällä jännenelikulmiota \(AA'C'C\) saadaan \[\angle C'A'B' = 180^{\circ} - \angle ACC' = \angle OCA\] ja jännenelikulmiosta \(BB'C'C\) saadaan \[\angle A'B'C' = 180^{\circ} - \angle C'B'B = \angle BCC'.\] Enää todetaan, että koska \(\angle ACB = 90^{\circ}\), niin kulmien \(\angle OCA\) ja \(\angle BCC'\) summa on \(90\) astetta. Yllä saatujen yhtälöiden nojalla nyt myös kulmien \(\angle C'A'B'\) ja \(\angle A'B'C'\) summa on \(90\) astetta, eli \(\angle B'C'A'\) on suora kulma.
Lauseen todistus on valmis!
32.4 Esimerkkitehtävä
Esitetään sitten esimerkkitehtävä, jossa inversiota käytetään tositilanteessa.
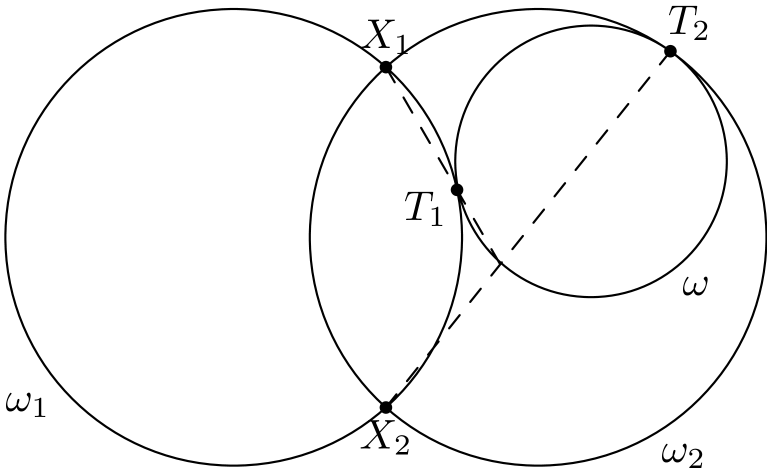
Ratkaisun rakenne on seuraava: suoritetaan inversio, jonka jälkeen saadaan toisenlainen ongelma, joka osataan ratkaista. (Ratkaisu on kuitenkin pitkä, koska inversion suorittaminen vaatii tekemistä. Lisäksi alussa pohditaan hieman, miksi inversio toimii ja miten inversio kannattaa tehdä.)
Mikä tekee tehtävästä niin otollisen inversiolle? Lyhyt vastaus: kuviossa on paljon ympyröitä.
Pidempi vastaus: Inversion avulla voimme muuttaa ympyröitä suoriksi (lauseen kohta (vi)). Kuviosta tekee erityisen vaikean se, että siinä on ympyröiden sivuamispisteitä. Tilanne on kuitenkin paljon helpompi, jos toinen ympyröistä saadaan inversion avulla muutettua suoraksi. Tällöin tutkittavaksi jää ympyrä ja sen tangentti, mikä on paljon tutumpi kuvio.
Suoritetaan siis inversio. Minkä ympyrän suhteen? Tämä on hieman huono kysymyksen asettelu. Yleensä oleellisinta on miettiä, mikä valitaan ympyrän keskipisteeksi. Ympyrän säteellä on harvemmin väliä.
Keskipisteeksi kannattaa valita sellainen piste, jonka kautta kulkee paljon ympyröitä (jotta lauseen kohdan (vi) avulla ne saadaan muutettua suoriksi, jolloin niitä on helpompi käsitellä). Jokaisen pisteistä \(X_1, X_2, T_1\) ja \(T_2\) kautta kulkee kaksi ympyrää, joten kannattaa valita jokin niistä. Vaihtoehdot on siis saatu rajattua neljään. Lisäksi pisteet \(X_1\) ja \(X_2\) ovat symmetrisiä toistensa suhteen (ja pisteet \(T_1\) ja \(T_2\) ovat myös melkein symmetrisiä toisiinsa nähden). Vaihtoehtoja on siis käytännössä vain pari: valitaan joko \(X_1\) tai \(T_1\). Tässä tutkitaan inversiota, jonka keskipiste on \(X_1\).1
1 Miksi \(X_1\) eikä \(T_1\)? Tämän voi löytää kokeilemalla (kaksi vaihtoehtoa ei ole niin paljon). Toinen tapa on ottaa huomioon, että ympyröillä \(\omega_1\) ja \(\omega_2\) on sama säde. Inversio \(X_1\) keskipisteenä säilyttää symmetrian näiden ympyröiden välillä, kun taas jos \(T_1\) olisi keskipiste, niin tätä tietoa olisi vaikea hyödyntää.
Suoritamme siis inversion, jonka inversioympyrän keskipiste on \(X_1\). Säteellä ei ole väliä – valitaan vaikka säde niin, että ympyrä kulkee pisteen \(X_2\) kautta. Mietitään sitten, mitä kuvan suorille ja ympyröille tapahtuu.
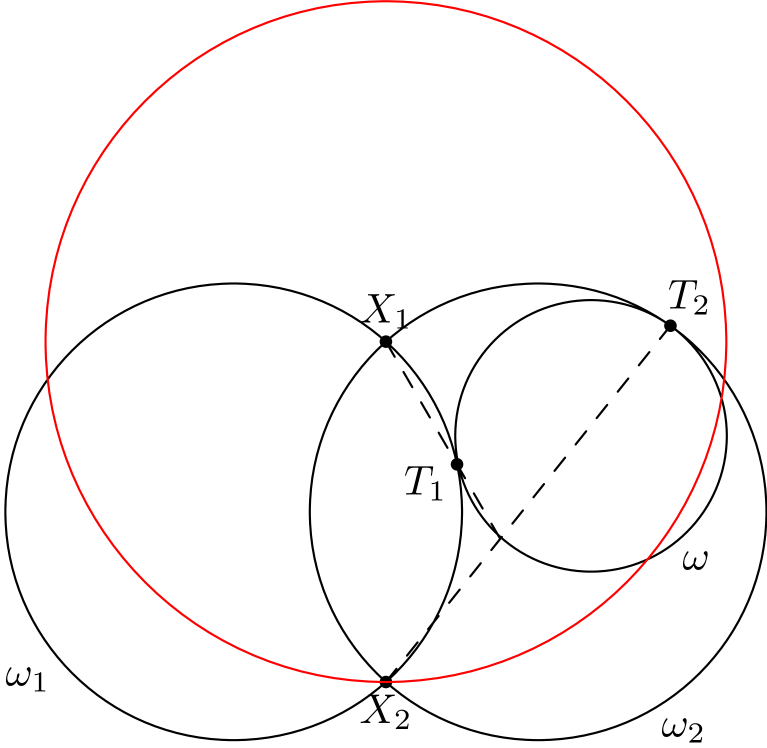
- \(X_2\):n kuva \(X_2'\) on sama kuin \(X_2\).
- \(T_1'\) on piste puolisuoralla \(X_1T_1\) (jossakin punaisen ympyrän ulkopuolella).
- \(T_2'\) on piste puolisuoralla \(X_1T_2\) (jossakin punaisen ympyrän ulkopuolella).
- Ympyrä \(\omega_1\) kuvautuu suoraksi (lauseen kohta (vi)). Tämä suora kulkee pisteiden \(X_2'\) ja \(T_1'\) kautta, koska pisteet \(X_2\) ja \(T_1\) ovat ympyrällä \(\omega_1\).
- Ympyrä \(\omega_2\) kuvautuu suoraksi (lauseen kohta (vi)). Tämä suora kulkee pisteiden \(X_2'\) ja \(T_2'\) kautta, koska pisteet \(X_2\) ja \(T_2\) ovat ympyrällä \(\omega_2\).
- Ympyrä \(\omega\) kuvautuu ympyräksi (lauseen kohta (vii)). Tämä ympyrä kulkee pisteiden \(T_1'\) ja \(T_2'\) kautta. Lisäksi se sivuaa niitä suoria, joiksi \(\omega_1\) ja \(\omega_2\) kuvautuvat, koska \(\omega\) sivuaa ympyröitä \(\omega_1\) ja \(\omega_2\).
Vielä yksi juttu: Tehtävänannossa on mainittu, että ympyröiden \(\omega_1\) ja \(\omega_2\) säteet ovat samat. Tämä tarkoittaa, että ne ovat symmetrisiä suoran \(X_1X_2\) suhteen. Tästä seuraa, että ympyröiden kuvaukset ovat myös symmetrisiä eli että \(X_1X_2'\) puolittaa suorien \(\omega_1'\) ja \(\omega_2'\) välisen kulman.
Yhdistämällä nämä tiedot saadaan seuraava kuva, joka kertoo tilanteen inversion jälkeen.
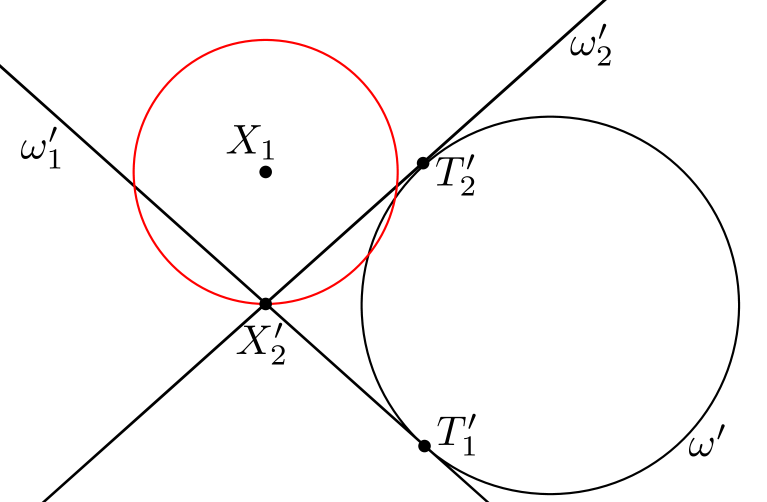
Nyt meillä on siis aivan uusi kuvio ja aivan uusi tehtävä. Ratkaistaan se!
Paitsi vielä pitää miettiä, mikä todistettava väite oikeastaan on. Alkuperäisessä tehtävässä halusimme todistaa, että suorat \(X_1T_1\) ja \(X_2T_2\) ja ympyrä \(\omega\) leikkaavat samassa pisteessä. Inversion jälkeen
- suora \(X_1T_1\) vastaa suoraa \(X_1T_1'\) (lauseen kohta (iii))
- suora \(X_2T_2\) vastaa kolmion \(X_1X_2'T_2'\) ympärysympyrää (lauseen kohta (v))
- ympyrä \(\omega\) vastaa inversion jälkeisen kuvion ympyrää \(\omega'\).
Todistettava väite voidaan siis kirjoittaa seuraavasti: Olkoon \(K\) on kuvion ympyrän ja kolmion \(X_1X_2'T_2'\) ympärysympyrän leikkauspiste. Osoita, että pisteet \(X_1, K\) ja \(T_1'\) ovat samalla suoralla.
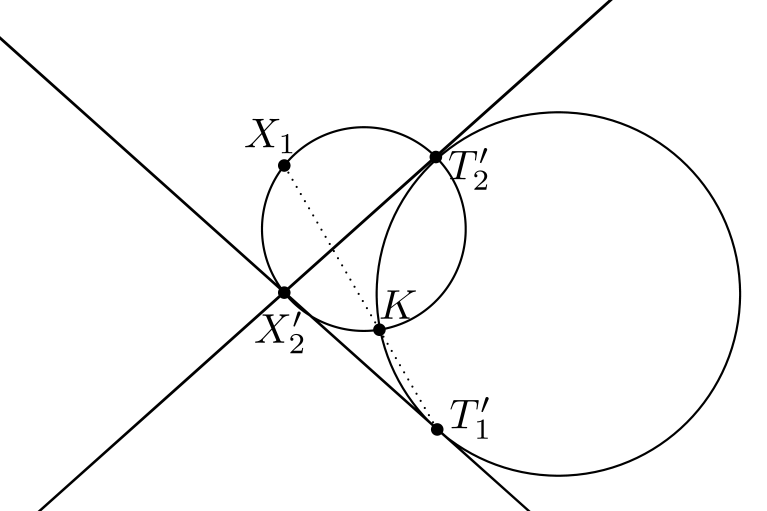
Tämä uusi tehtävä ei ole kovin vaikea: se oikeastaan ratkeaa suoraan kulmanjahtauksella. Alla on yksityiskohdat. (Lukija voi yrittää ratkoa tehtävän itse ennen ratkaisun lukemista.)
Ratkaisu. Merkitään \(\alpha = \angle T_2'X_2'X_1\), jolloin suorien väliset kulmat ovat \(2\alpha\) ja \(180^{\circ} - 2\alpha\).
Tavoitteena on osoittaa, että \[ \angle T_2'KX_1 = \alpha \qquad(32.1)\] ja \[ \angle T_1'KT_2' = 180^{\circ} - \alpha. \qquad(32.2)\] Näistä seuraa, että \(T_1'KX_1 = 180^{\circ}\), mikä on todistettava väite.
Väite 32.1 seuraa suoraan jännenelikulmiosta \(X_1X_2'KT_2'\) kehäkulmalauseella: \(\angle T_2'KX_1 = \angle T_2'X_2'X_1 = \alpha\).
Väite 32.2 vaatii enemmän työtä. Koska \(X_2'T_1'\) ja \(X_2'T_2'\) ovat tangentteja ympyrälle, ne ovat yhtä pitkiä ja \(X_2'T_1'T_2'\) on tasakylkinen kolmio. Täten \[\angle T_2'T_1'X_2' = \angle X_2'T_2'T_1' = \alpha.\] Nyt käyttämällä kehäkulmalauseen tangenttiversiota saadaan, että kolmion \(KT_1'T_2'\) lyhyempää kaarta \(T_1'T_2'\) vastaavan kehäkulman suuruus on \(\alpha\). Täten pidempää kaarta vastaava kehäkulma on \[\angle T_1'KT_2' = 180^{\circ} - \alpha,\] mikä on haluttu väite.
Ratkaisu on vihdoin valmis!
32.5 Tehtäviä
Loppupään tehtävissä on saatavilla vihje, joka kertoo, minkä ympyrän suhteen inversio kannattaa tehdä.
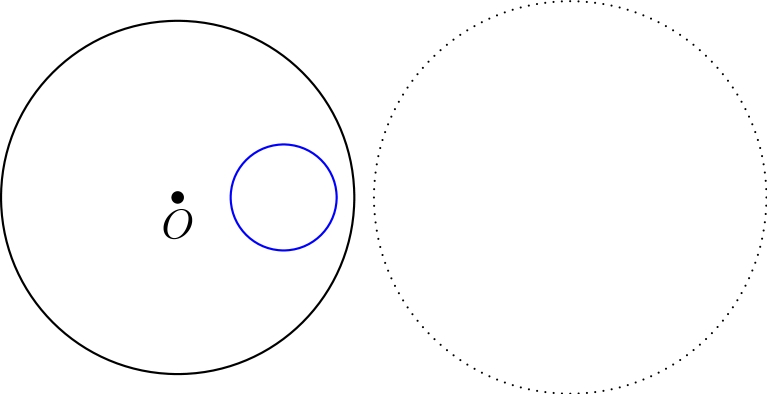
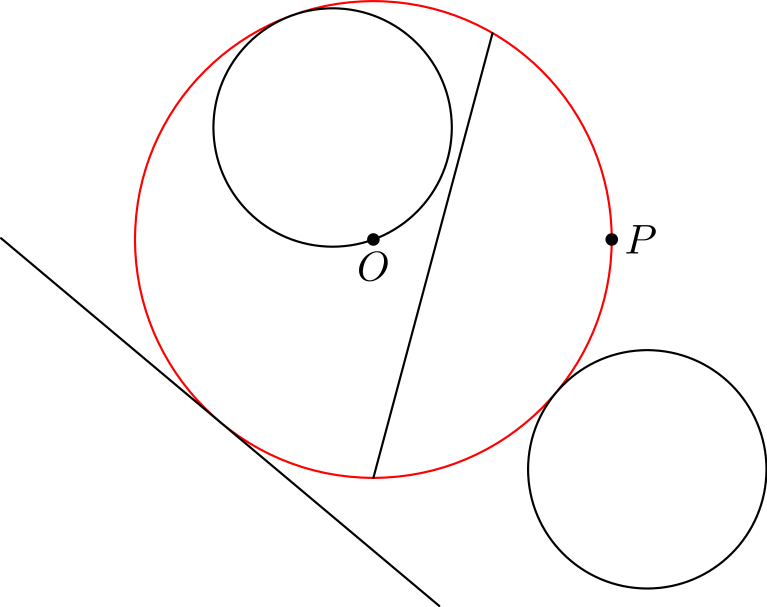
Tehtävä 1. Alla olevassa kuvassa on annettu \(O\)-keskinen ympyrä (punaisella) sekä muita muotoja. Hahmottele mielessäsi, miltä muotojen inversiot näyttävät ja mihin ne sijoittuvat, kun suoritetaan inversio punaisen ympyrän suhteen.
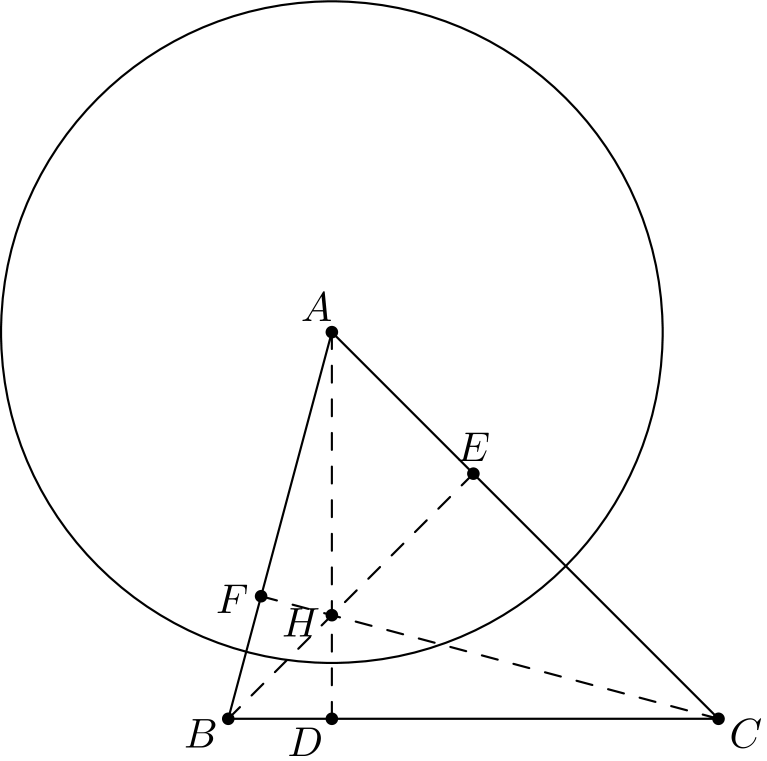
Tehtävä 2. Janat \(AD, BE\) ja \(CF\) ovat (teräväkulmaisen) kolmion \(ABC\) korkeusjanat. Tehdään inversio, jonka keskipiste on \(A\) ja säde \(\sqrt{AD \cdot AH}\). Mihin pisteet \(B, C, D, E, F\) ja \(H\) kuvautuvat?
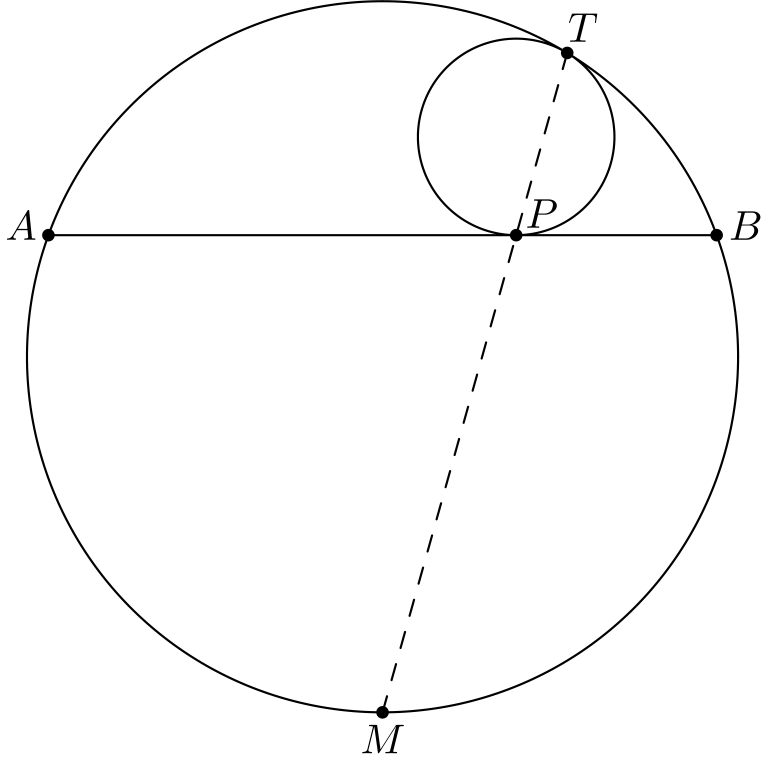
Tehtävä 3. Ympyrällä on jänne \(AB\). Piirretään pienempi ympyrä, joka on tangentti jänteelle \(AB\) pisteessä \(P\) ja ympyrälle pisteessä \(T\). Olkoon \(M\) sen kaaren \(AB\), joka ei sisällä pistettä \(T\), keskipiste. Osoita, että \(M, P\) ja \(T\) ovat samalla suoralla.
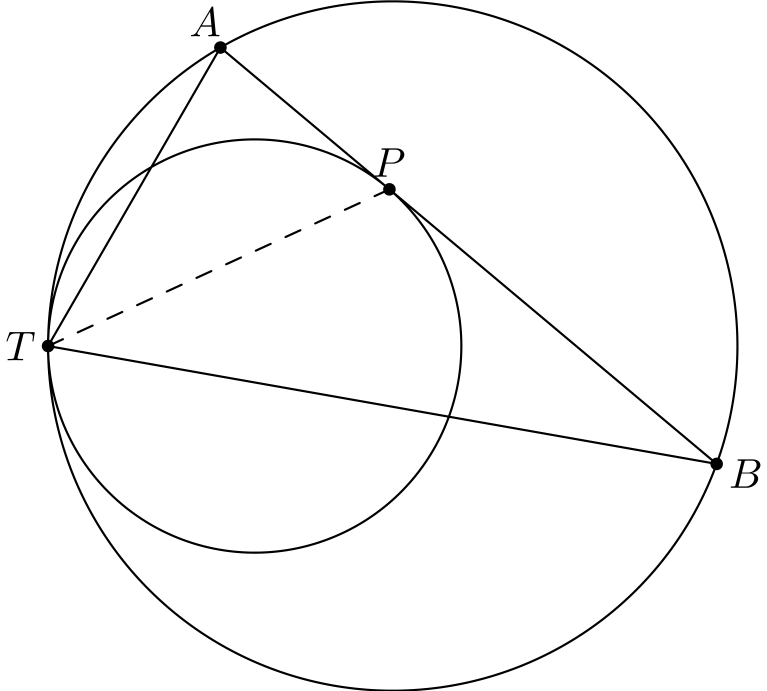
Tehtävä 4. Kaksi ympyrää sivuaa toisiaan sisäpuolisesti pisteessä \(T\). Ulomman ympyrän jänne \(AB\) sivuaa sisempää ympyrää pisteessä \(P\). Osoita, että suora \(TP\) puolittaa kulman \(\angle BTA\).
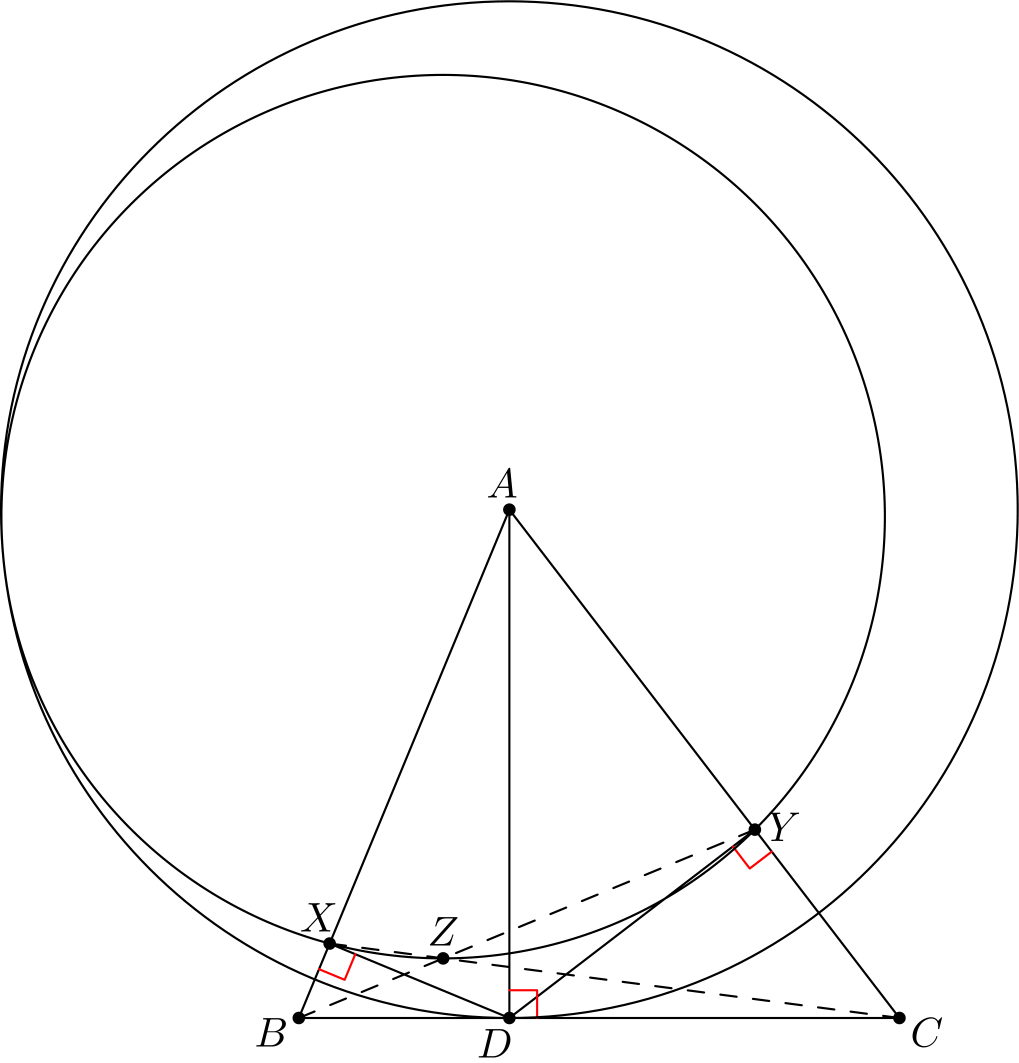
Tehtävä 5. Olkoon \(ABC\) kolmio. Olkoon \(D\) kärjestä \(A\) piirretyn korkeusjanan kanta ja olkoot \(X\) ja \(Y\) pisteestä \(D\) janoille \(AB\) ja \(AC\) piirrettyjen korkeusjanojen kantapisteet. Olkoon \(Z\) janojen \(BY\) ja \(CX\) leikkauspiste. Olkoon \(\omega_1\) ympyrä, jonka keskipiste on \(A\) ja säde \(AD\), ja olkoon \(\omega_2\) kolmion \(XYZ\) ympärysympyrä. Osoita, että \(\omega_1\) ja \(\omega_2\) sivuavat toisiaan.