5 Laatikkoperiaate

Tekijä

Olli Järviniemi

5.1 Johdanto

Laatikkoperiaate on konseptina hyvin yksinkertainen: jos laitamme kolmeen laatikkoon yhteensä neljä palloa, tulee johonkin laatikkoon laitettua vähintään kaksi palloa. Tästä huolimatta periaatetta voi hyödyntää vaikeissa tehtävissä valitsemalla laatikot ja pallot sopivasti. Alla esitetään pari ovelaa sovellusta. Lopussa on tietysti tehtäviä, joista lukija löytää lisää käyttökohteita.

5.2 Laatikkoperiaate

Laatikkoperiaate sanoo seuraavaa:

Lause 5.1 (Laatikkoperiaate, muotoilu 1) Jos \(n\) laatikkoon laitetaan yhteensä \(n+1\) palloa, niin on olemassa vähintään yksi laatikko, jossa on vähintään kaksi palloa.

(Koska jos ei olisi, niin kussakin laatikossa olisi enintään yksi pallo, eli palloja olisikin yhteensä enintään \(n\).)

Lause 5.2 (Laatikkoperiaate, muotoilu 2) Jos \(n\) laatikkoon laitetaan yhteensä \(m\) palloa, niin on olemassa vähintään yksi laatikko, jossa on vähintään \(\frac{m}{n}\) (pyöristettynä ylöspäin) palloa.

(Koska jos ei olisi, niin kussakin laatikossa olisi alle \(\frac{m}{n}\) palloa, eli palloja olisi yhteensä alle \(m\). Voimme pyöristää ylöspäin seuraavaan kokonaislukuun, koska pallojen määrä on kokonaisluku.)

Siis jos esimerkiksi neljään laatikkoon laitetaan yhdeksän palloa, niin johonkin laatikkoon tulee vähintään \(\frac{9}{4} = 2{,}25\) palloa pyöristettynä ylöspäin, eli vähintään kolme palloa. Kuten jo mainittiin, ei kuulosta kovin ihmeelliseltä, mutta esimerkit ovat silti mielenkiintoisia.

5.3 Esimerkki 1: Pisteet neliössä

Tehtävä 5.1 Neliön sivun pituus on yksi. Neliön sisällä on \(51\) pistettä. Osoita, että riippumatta pisteiden sijainneista löytyy jotkin kolme pistettä, jotka voidaan peittää ympyrällä, jonka säde on \(\frac{1}{7}\).

Toisin sanoen joidenkin kolmen pisteen pitäisi olla kohtuullisen lähellä toisiaan.

Idea on seuraava: Yritetään peittää neliö mahdollisimman pienellä määrällä sellaisia ympyröitä, joiden säde on \(\frac{1}{7}\). Tällöin laatikkoperiaate sanoo, että jossain ympyrässä on varmasti melko paljon pisteitä.

Yritetään toteuttaa tämä idea. Kuinka monta ympyrää meillä on käytettävissä? Kuvitellaan, että saamme tehtyä peittämisen \(n\) kappaleella ympyröitä. Tällöin jossakin ympyrässä on vähintään \(\frac{51}{n}\) pistettä (pyöristettynä ylöspäin). Kunhan \(\frac{51}{n} > 2\), niin pyöristys ylöspäin on (vähintään) kolme. Tämä epäyhtälö toteutuu, kun \(n = 25\), muttei enää kun \(n = 26\). Käytössämme on siis \(25\) ympyrää.

Ympyrät kannattaisi varmankin sijoittaa tasaisesti yksikköneliön sisälle. Yksi luonnollinen idea tämän saavuttamiseksi on jakaa yksikköneliö \(25\) neliöön, joiden jokaisen sivun pituus on \(\frac{1}{5}\), ja asettaa ympyröiden keskipisteet näiden pikkuneliöiden keskipisteisiin.

Nyt kysymys kuuluu: saako kunkin pikkuneliön peitettyä yhdellä ympyrällä?

Vastaus kysymykseen on myönteinen. Tilanne on esitettynä seuraavassa kuvassa.

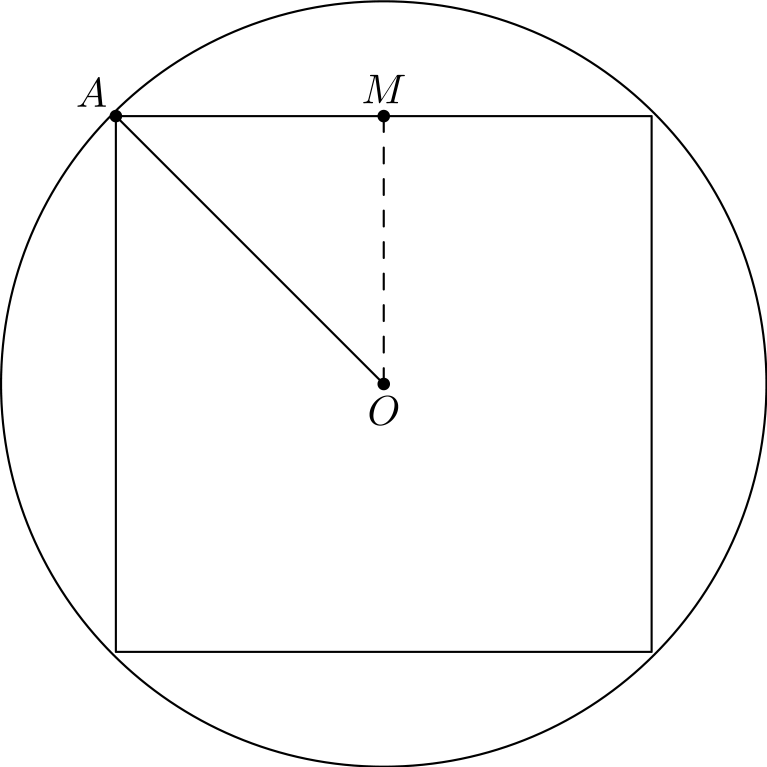
Kuvaan on merkitty neliön ja ympyrän keskipiste \(O\), neliön kärkipiste \(A\) ja yhden neliön sivun keskipiste \(M\). Riittää tietysti todistaa, että jokainen neliön kärkipisteistä on ympyrän sisäpuolella. Haluamme siis osoittaa, että \(AO \le \frac{1}{7}\).

Pituus \(AO\) osataan laskea kolmiosta \(AMO\) käyttämällä Pythagoraan lausetta. Janat \(AM\) ja \(MO\) ovat pituudeltaan puolet neliön sivun pituudesta \(\frac{1}{5}\), eli \(AM = MO = \frac{1}{10}\). Pythagoraan lause antaa \[AO^2 = AM^2 + MO^2 = \frac{1}{100} + \frac{1}{100} = \frac{1}{50}.\] Täten \(AO = \frac{1}{\sqrt{50}}\). Tämä on pienempi kuin \(\frac{1}{7}\), koska \(\sqrt{50} > 7\). (Ero on kuitenkin hyvin pieni, kuten kuvastakin nähdään.) Tehtävä on täten ratkaistu.

5.4 Esimerkki 2: Lukuja ja jaollisuutta

Seuraava esimerkki on aika vaikea.

Tehtävä 5.2 Luvuista \(1, 2, \ldots , 100\) valitaan jotkin niin, ettei mitkään kaksi eri lukua jaa toisiaan. Kuinka monta lukua voidaan enimmillään valita?

On hyvä idea yrittää ensin keksia vastaus. Yksi luonteva veikkaus voisi olla valita kaikki alkuluvut väliltä yhdestä sataan. On kuitenkin myös parempia ratkaisuja, joilla saa useamman luvun valittua. Kokeilemalla eri ideoita voi löytää näitä parempia ratkaisuja, mutta on myös melko varma tapa löytää parhaat ratkaisut: tutkitaan pieniä tapauksia.

Tutkitaan siis tapausta, jossa lukujen \(1, 2, \ldots , 100\) sijasta valitaan lukuja \(1, 2, \ldots , n\). Tässä on listattu parhaita ratkaisuja pienillä luvun \(n\) arvoilla. (Parhaita ratkaisuja voi olla useampia.)

\(n = 1\): valitaan \(1\)
\(n = 2\): valitaan \(1\)
\(n = 3\): valitaan \(2, 3\)
\(n = 4\): valitaan \(3, 4\)
\(n = 5\): valitaan \(3, 4, 5\)
\(n = 6\): valitaan \(4, 5, 6\)

Säännönmukaisuus alkaa ehkä hahmottua: voidaan aina valita noin puolet luvuista valitsemalla kaikkein isoimmat luvut. Alkuperäisessä tehtävässä voidaan siis valita luvut \(51, 52, 53, \ldots , 100\).

Yritetään osoittaa, että useampaa kuin viittäkymmentä lukua ei saa valittua. Yritetään käyttää tähän laatikkoperiaatetta valitsemalla ”laatikot” sopivasti. Ei ole kuitenkaan selvää, miten laatikot tulee valita.

Niin, miten oikeastaan haluamme valita laatikot? Tai mitä laatikot oikeastaan edes ovat?

Suunnitelma on jakaa luvut \(1, 2, \ldots , 100\) laatikkoihin niin, että pääsemme käyttämään laatikkoperiaatetta. Kuinka monta laatikkoa on käytettävissä? \(50\) laatikkoa vaikuttaa hyvältä, koska tällöin \(51\) luvusta jotkin kaksi kuuluvat samaan laatikkoon. Jotta laatikkoperiaatteen soveltaminen antaa varmasti kaksi toisensa jakavaa lukua, pitää jokaisessa laatikossa mistä tahansa kahdesta luvusta toisen jakaa toinen.

Ryhdytään toimeen ja yritetään jakaa luvut \(1, 2, \ldots ,100\) viiteenkymmeneen laatikkoon niin, että saman laatikon luvuista toinen aina jakaa toisen. On hyvä idea yrittää aina laittaa yhteen laatikkoon niin paljon lukuja kuin pystyy, jotta laatikoita tulee käytettyä tehokkaasti siten, etteivät ne lopu kesken. Laitetaan siis aina laatikkoon pienin luku, joka sinne voidaan laittaa niin, että haluttu ehto toteutuu. Tämä tarkoittaa seuraavaa:

Luvun \(1\) sisältävään laatikkoon laitetaan luku \(2\), sitten luku \(4\), sitten \(8\), \(16\), \(32\) ja \(64\).

Seuraava luku, joka ei ole vielä laatikossa, on \(3\). Tämän kanssa laitetaan luku \(6\), sitten \(12, 24, 48\) ja \(96\).

Seuraava puuttuva luku on \(5\), ja samaan laatikkoon laitetaan luvut \(10, 20, 40\) ja \(80\).

Seuraava laatikko sisältää luvut \(7, 14, 28, 56\).

Seuraava laatikko sisältää luvut \(9, 18, 36, 72\).

Ja niin edelleen. Huomataan, että laatikot alkavat aina parittomasta luvusta ja laatikossa seuraava luku on aina kaksi kertaa edellinen. Laatikoita on siis yhtä monta kuin parittomia lukuja välillä yhdestä sataan, eli \(50\). Tämä on juuri haluttu määrä. Olemme valmiit.

5.5 Tehtäviä

Monessa tehtävässä avainkysymyksenä on miten valita laatikot. Pidemmälle mentäessä tehtävissä vaaditaan enemmän luovuutta.

Tehtävä 1. Luvuista \(1, 2, \ldots , 100\) valitaan jokin määrä lukuja. Käy niin, ettei minkään kahden valitun luvun summa ole \(101\). Kuinka monta lukua voidaan enimmillään valita?

Tehtävä 2. Taloja numeroidaan. Jokaiselle talolle annetaan talonumeroksi jokin kokonaisluku yhden ja viidenkymmenen väliltä. Millekään kahdelle talolle ei anneta samaa numeroa (joten taloja on korkeintaan \(50\)). Tiedetään, että on jotkin viisi taloa, joiden talonumerot ovat peräkkäiset. Kuinka monta taloja vähintään on?

Tehtävä 3. Luvuista \(1, 2, \ldots , 20\) valitaan jokin määrä lukuja. Käy niin, että minkä tahansa kahden (eri) valitun luvun suurin yhteinen tekijä on \(1\). Kuinka monta lukua voidaan enimmillään valita?

Tehtävä 4. Neliön sivun pituus on kaksi. Neliön sisältä (tai sen reunoilta) valitaan viisi pistettä. Osoita, että jotkin kaksi näistä pisteistä ovat enintään etäisyyden \(\sqrt{2}\) päässä toisistaan.

Tehtävä 5. Neliönmuotoisella \(10 \times 10\) -kokoisella niityllä kasvaa kukkia. Minkä tahansa kahden kukan välinen etäisyys on vähintään \(1\). Osoita, että niityllä on enintään \(250\) kukkaa.

Bonustehtävä: Saatko parannettua ylärajaa? Kuinka paljon?

Tehtävä 6. Juhlissa on kymmenen ihmistä. Jotkin heistä ovat ystäviä keskenään. (Ystävyys on molemminpuolista: jos \(A\) on \(B\):n ystävä, niin myös \(B\) on \(A\):n ystävä. Kukaan ei ole ystävä itsensä kanssa.) Osoita, että juhlista voidaan valita kaksi henkilöä, joilla on yhtä monta ystävää.

Tehtävä 7. \(8 \times 8\) -shakkilaudalle asetetaan shakkikuninkaita niin, etteivät mitkään kaksi niistä uhkaa toisiaan. (Kaksi kuningasta uhkaavat toisiaan, jos ne ovat ruuduissa, jotka ovat pysty-, vaaka- tai vinosuunnassa vierekkäisiä.) Kuinka monta kuningasta laudalle voidaan enimmillään laittaa?

Tehtävä 8. Lukusuoralle on merkitty eri lukuja. Minkä tahansa kahden (eri) merkityn luvun \(a\) ja \(b\) etäisyys on yli kaksi ja alle seitsemän (eli \(2 < |a - b| < 7\)). Osoita, että merkittyjä lukuja on enintään neljä.