26  Prosessit ja algoritmit

26.2 Invariantit

Invariantti: suure, joka ei muutu prosessin aikana.

Laatoitukset ovat klassisia esimerkkejä invarianteista: värittämällä ruudukko sopivasti huomataan, ettei sen laatoittaminen tietyillä palikoilla onnistu. Otetaan tästä esimerkki.

On helppo keksiä laatoitus tapauksessa, jossa keskimmäinen ruutu poistetaan. Mutta miksei laatoitus onnistu muissa tapauksissa? Tutkitaan esimerkki­tapausta.

Ideana on värittää laudan ruudut siten, että osaamme sanoa jotakin siitä, montako kunkin värin ruutua jokainen laatta peittää. Luonteva idea on värittää lauta kolmella värillä niin, että kukin laatta peittää yhden ruudun kutakin väriä. Tämä onnistuu seuraavasti:

Jokainen $1 \times 3$ -laatta peittää yhden ruudun kutakin väriä. Punaisia ruutuja on kuitenkin $9$ ja sinisiä $7$, joten toisaalta peittämiseen tulisi käyttää $9$ laattaa ja toisaalta $7$. Tämä ei tietysti käy.

Koko tehtävän saa ratkaistua tällä idealla. Tutkitaan alla olevia värityksiä.

Kummassakin värityksessä on $9$ punaista ruutua ja $8$ sinistä ja $8$ vihreää ruutua. Jotta laatoitus onnistuu, tulee laudalta poistaa sellainen ruutu, joka on punainen sekä vasemmassa että oikeassa värityksessä. Ainoa tällainen ruutu on laudan keskimmäinen ruutu, eli laatoitus onnistuu vain jos keskimmäinen ruutu poistetaan.

Tässä on toinen esimerkki­tehtävä, joka on enemmän prosessimainen.

Tehtävässä on kätkettynä jokin invariantti: riippumatta siitä, mitä Anna tekee, jokin suure pysyy samana. Mikä tämä suure on?

Pyöritellään ideoita mielessä. Mitä suureita ylipäätään pystymme muodostamaan luvuista? Voimme tutkia lukujen summaa. Tämä ei tietenkään pysy samana: $AB + A + B \neq A + B$. Huomataankin, että luvut kasvavat hyvin nopeasti, minkä takia summa ei todellakaan toimi.

Kasvu­nopeudesta johtuen lukujen tulo tuntuu paremmalta idealta, mutta tämäkään ei toimi, koska $AB + A + B \neq A \cdot B$. Tämä on kuitenkin jo lähempänä: $AB + A + B$ ja $AB$ ovat kohtalaisen lähellä toisiaan.

Suure todennäköisesti liittyy jotenkin lukujen tuloihin, muttei ole selvää miten. Voi auttaa tutkia pieniä tapauksia, joissa taululla on aluksi vähemmän kuin sata lukua. Lopussa olevan luvun selvittämiseksi riittää käydä vain yksi skenaario läpi, koska vastaus ei tehtävän­annon mukaan riipu järjestyksestä (vaikkemme tätä vielä osaakaan todistaa).

• Taululla on aluksi luvut $1$ ja $2$. Lukujen tulo on $2$. Lopuksi taululla on luku $5$.
• Taululla on aluksi luvut $1, 2$ ja $3$. Lukujen tulo on $6$. Lopuksi taululla on luku $23$.
• Taululla on aluksi luvut $1, 2, 3$ ja $4$. Lukujen tulo on $24$. Lopuksi taululla on luku $119$.
• Taululla on aluksi luvut $1, 2, 3, 4$ ja $5$. Lukujen tulo on $120$. Lopuksi taululla on luku $719$.

Säännön­mukaisuus alkaa erottumaan: lukujen ollessa $1, 2, \ldots , n$ on vastaus $$(n+1)! - 1 = 1 \cdot 2 \cdot 3 \cdot \ldots \cdot (n+1) - 1.$$ Lukuja tulee siis jotenkin kasvattaa yhdellä.

Tästä keksitään ratkaisu: haluttu suure on tulo luvuista, jotka vastaavat taulun lukuja mutta joihin on jokaiseen lisätty yksi. Pätee nimittäin $AB + A + B + 1 = (A+1)(B+1)$. Tämä suure ei muutu ja aluksi se on $(n+1)!$. Täten lopussa olevan luvun tulee olla $(n+1)! - 1$.

Esitetään vielä yksi opettavainen esimerkki samasta teemasta.

Voitto­strategia Annalle tapauksessa $k = 2^n$ (ja siten tapauksessa $k \ge 2^n$) on helppo keksiä: jaetaan nykyinen joukko aina kahtia, jolloin toinen puolisko pääsee yhden askeleen eteenpäin. Tällöin aina ruutuun $i$ siirretään $2^{n - i}$ kolikkoa, joten ruutuun $n$ siirretään $2^0 = 1$ kolikko.

Tapauksessa $k < 2^n$ pitää keksiä Bellalle voitto­strategia. Parikin strategiaa tulee mieleen:

• Bella poistaa aina sen joukon, jossa on etummaisin kolikko (ja tasa­tilanteet käsitellään jotenkin).
• Bella poistaa aina sen joukon, jossa on enemmän kolikoita (ja tasa­tilanteet käsitellään jotenkin).

Ikävä kyllä kumpikaan näistä ei toimi: Anna voi antaa Bellalle ”syöttejä” ja näin hyödyntää Bellan strategian heikkouksia.

Ongelma on siinä, etteivät strategiat ota kunnolla huomioon kokonais­kuvaa. Ensimmäinen strategia ottaa huomioon vain etummaiset kolikot. Toinen strategia sentään katsoo kolikoiden määriä, muttei ota niiden sijainteja kunnolla huomioon. Seuraava ratkaisu korjaa nämä ongelmat ottaen jokaisen kolikon sijainnin huomioon.

Määritellään kolikon tärkeys olemaan $2^m$, missä $m$ on kolikon nykyinen ruutu. Bellan strategia on aina poistaa se kolikko­joukko, jonka kolikoiden tärkeyksien summa on suurempi (tasa­tilanteessa poistetaan kumpi tahansa).

Väite. Kun Bella pelaa näin, laudalla olevien kolikoiden tärkeyksien summa ei koskaan kasva.

Väitteen perustelu. Oletetaan, että Anna valitsee kolikko­joukot $A$ ja $B$, joiden kolikoiden tärkeyksien summat ovat $a$ ja $b$. Jos $a \ge b$, Bella poistaa joukon $A$ kolikot, ja $B$:n kolikot siirtyvät yhden askeleen eteenpäin. Joukon $B$ jokaisen kolikon tärkeys kaksin­kertaistuu, joten tärkeyksien summakin kaksin­kertaistuu, eli lisääntyy $b$:llä. Täten tärkeyksien summan muutos on $-a + b \le 0$. Tapaus $b \ge a$ on symmetrinen.

Ratkaisun viimeistely. Alussa tärkeyksien summa on $k < 2^n$. Jos Anna saisi jossakin vaiheessa kolikon ruutuun $n$, olisi tämän kolikon tärkeys $2^n$. Tämä on risti­riidassa sen kanssa, ettei tärkeyksien summa kasva.

26.3 Muita esimerkkejä

Ennen väitteen todistamista pohditaan hetki, mitä prosessissa oikein tapahtuu. Lähteekö prosessi edes liikkeelle? Lähtee: Jos jossakin ruudussa on vähintään $8$ sammakkoa, ruudusta hyppää sammakoita muualle. Koska alussa sammakoita on tuhat ja ruutuja sata, on jossakin ruudussa aluksi vähintään kahdeksan (ja jopa vähintään kymmenen) sammakkoa.

Samaan tapaan huomataan, että prosessi ei pääty missään vaiheessa.

Väitteen todistamiseksi voisi miettiä, missä ruuduissa käy vähintään yksi sammakko. Tämä ei kuitenkaan kerro juuri mitään.

Sen sijaan parempi kysymys on miettiä, mihin ruutuihin tulee prosessin aikana sammakko äärettömän monta kertaa. Tiedämme, että vähintään yksi tällainen ruutu on olemassa, koska prosessi jatkuu loputtomiin. Ei ole myöskään vaikea nähdä, että jos ruudulla on tämä ominaisuus, niin myös ruudun naapureilla on tämä ominaisuus, koska ruudusta hyppii sen naapureihin äärettömän monta sammakkoa prosessin aikana.

Tästä seuraa, että jokaiseen ruutuun hyppää prosessin aikana äärettömän monesti sammakko.

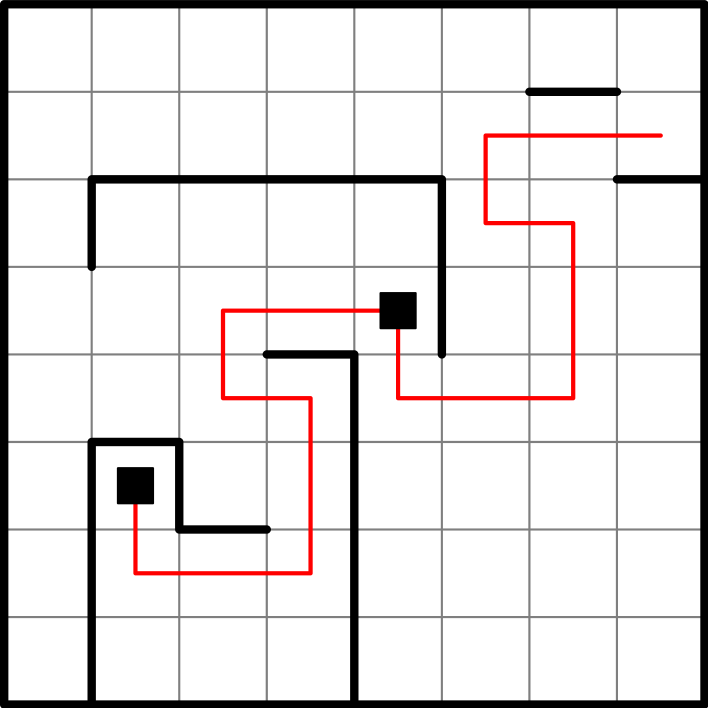
Yllä oleva kuva esittää yhden esimerkki­tapauksen. Esimerkki ei ole kovin vaikea: voimme vaikkapa aluksi tehdä kolme askelta vasemmalle ja kolme askelta alas, jolloin kaksi robottia saadaan samaan ruutuun vasempaan ala­nurkkaan. Tämän jälkeen tekemällä kolme askelta ylös ja kolme vasemmalle saadaan kolmaskin robotti samaan ruutuun.

Yleisesti huomataan, että riittää ratkaista tehtävä kahden robotin tapauksessa. Jos nimittäin robotit jossain kohtaa päätyvät samaan ruutuun, ne ovat aina samassa ruudussa.

Kahden robotin tapaus ei ole aivan helppo. Esimerkiksi yksin­kertainen suunnitelma ”kuljetetaan ensiksi toinen roboteista vasempaan ala­nurkkaan, ja viedään sitten toinenkin roboteista sinne” ei välttämättä toimi: ensimmäinen robotti saattaa (ainakin periaatteessa) ”karata” sillä välin kun keskitytään toiseen robottiin.

Mietitään asiaa toisesta näkö­kulmasta: yritetään saada robotit koko ajan lähemmäksi toisiaan.

Tarkemmin sanoen määritellään kahden ruudun etäisyydeksi pienin määrä askelia, joka tarvitaan ensimmäisestä ruudusta toiseen ruutuun pääsemiseksi. Tavoitteena on saada liikutettua robotteja niin, että niiden ruutujen väliset etäisyydet pienenevät.

Jos robottien etäisyys on aluksi yksi, eli esimerkiksi toinen roboteista on toisen oikealla puolella ja ruutujen välillä ei ole seinää, voidaan vain toistuvasti liikkua oikealle. Jossakin kohtaa etummaiselle robotille tulee seinä vastaan, jolloin robotit päätyvät samaan ruutuun.

Tutkitaan sitten yleisesti tilannetta, jossa robottien etäisyys on $n$, eli ensimmäisen robotin ruudusta pääsee toisen robotin ruutuun jollakin $n$ siirron sarjalla (muttei nopeampaa). Suoritetaan tämä $n$ siirron sarja. Mitä tapahtuu? Robottien etäisyys on siirto­sarjan jälkeen selvästikin enintään $n$. Jos se on alle $n$, olemme saaneet robotit lähemmäksi toisiaan.

Entä jos etäisyys on edelleen $n$? Tämä tarkoittaa, että toinen robotti ei törmännyt seinään kertaakaan siirto­sarjan aikana. Tämä puolestaan tarkoittaa, että (yksi) nopein tapa päästä ensimmäisen robotin ruudusta toiseen on käyttää samaa $n$ siirron sarjaa kuin aiemminkin. Suoritetaan siirto­sarja siis uudestaan ja tarvittaessa vielä useamman kerran uudestaan.

Voiko olla niin, että vaikka tämän siirto­sarjan tekisi kuinka monta kertaa tahansa, niin robottien etäisyys olisi edelleen $n$? Ei: siirto­sarjan seurauksena robotit kulkevat johonkin suuntaan aloitusruudusta. Toistamalla siirto­sarjaa robotit kulkevat pidemmälle ja pidemmälle tähän suuntaan. Jossakin vaiheessa ruudukon reuna tulee vastaan.

Siis toistamalla siirto­sarjaa riittävän monta kertaa saadaan robotit lähemmäksi toisiaan. Toistamalla samaa ideaa saadaan robotit yhä lähemmäs ja lähemmäs toisiaan, kunnes ne ovat samassa ruudussa.