30 Globaalit argumentit

Tekijä

Olli Järviniemi

30.1 Johdanto

Joissakin kombinatoriikan tehtävissä idea on katsoa kokonaiskuvaa. Saatetaan esimerkiksi ”summata kaikki”. Tällaisia menetelmiä kutsutaan globaaleiksi ideoiksi. Globaalin menetelmän vastakohta on lokaali menetelmä, jossa tutkitaan vain pientä osaa ongelmasta kerrallaan.

Globaalius ja lokaalius ovat pikemminkin ajatustyökaluja, joista on hyötyä joissain tilanteissa, kuin tarkkoja luokitteluja. Kyseessä on siis veteen piirretty viiva, mikä tekee konseptin oppimisesta¹ vaikeaa.

¹ Ja opettamisesta :-)

Alla esitetään esimerkkejä, jotka demonstroivat näitä ajatuksia.

30.2 Esimerkkitehtäviä

Tehtävä 30.1 Matematiikkakilpailussa on seitsemän tehtävää. Tiedetään, että kilpailijoista jokainen ratkaisi vähintään kolme tehtävää ja jokaista tehtävää kohden on olemassa enintään kolme henkilöä, jotka ratkaisivat tehtävän. Osoita, että kilpailuun osallistui enintään seitsemän kilpailijaa.

Tehtävää voi visualisoida ruudukkona, jossa on seitsemän saraketta ja yhtä monta riviä kuin kilpailijoita. Raksi kertoo, että kisaaja on ratkaissut tehtävän.

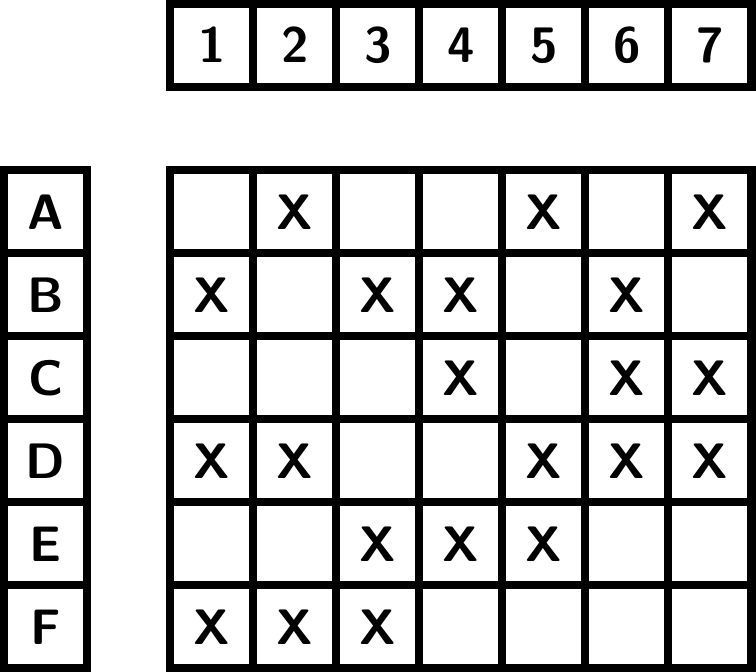
Tehtävän ratkeaa seuraavasti: Olkoot \(x_1, x_2, \ldots , x_7\) niiden kisaajien määrät, jotka ratkovat tehtävät \(1, 2, \ldots , 7\) (eli kussakin sarakkeessa olevien raksien määrät). Olkoot \(y_1, y_2, \ldots , y_n\) kunkin kisaajan ratkaisemien tehtävien määrät (eli kullakin vaakarivillä olevien raksien määrät). Tiedetään, että \(y_i \ge 3\) ja \(x_j \le 3\) kaikilla \(i\) ja \(j\). Lisäksi tiedetään, että \[x_1 + x_2 + \ldots + x_7 = y_1 + y_2 + \ldots + y_n.\] Tästä saadaan, ettei \(n\) voi olla liian suuri: vasen puoli on enintään \(21\) ja oikea puoli on vähintään \(3n\), joten \(n \le 7\).

Kommentti. Avainidea on siis tutkia kaikkia rivejä ja sarakkeita samanaikaisesti summaamalla vaaka- ja pystyrivien raksien määrät. Tämä on esimerkki globaalista argumentista.

Mitä muita lähestymistapoja tehtävään on? Yksi suorempi lähestymistapa on tutkia paria kisaajaa ja mitä tehtäviä he ovat ratkaisseet, ja yrittää saada tästä informaatiota koskien sitä, mitä muut kisaajat ovat ratkaisseet. Tämä on edelliseen ratkaisuun verrattuna lokaalimpi lähestymistapa: ei tutkita kaikkea samanaikaisesti vaan pienempää osaa tuloslistasta.

Voi ajatella, että lokaali lähestymistapa on ”hienovarainen”: esimerkiksi tässä tehtävässä tapauskäsittely ottaisi huomioon kunkin kisaajan erikseen. Sen sijaan globaali lähestymistapa on ”kovakourainen” ja se ei välitä yksittäisistä kisaajista: tehtävässä oleellista ei ollut se, että kukin kisaaja ratkaisi vähintään kolme tehtävää vaan ainoastaan se, että he ratkaisivat yhteensä vähintään \(21\) tehtävää.

Tässä tehtävässä on selvää (ainakin ratkaisun lukemisen jälkeen), että globaali menetelmä on ”oikea” tai ainakin riittävän hyvä lähestymistapa. Aina ei kuitenkaan ole selvää, millainen globaali idea tehtävään toimii (tai edes että tehtävää kuuluu ajatella globaalisti). Alla esitetään hieman vaikeampia esimerkkejä.

Tehtävä 30.2 \(100 \times 100\) -ruudukon kussakin ruudussa on jokin kokonaisluku. Missään kahdessa ruudussa ei ole samaa lukua. Ruudun naapureita ovat ne ruudut, joilla on yhteinen sivu tai kärkipiste ruudun kanssa. Osoita, että on olemassa jokin ruutu, jonka naapuriruutujen luvuista vähintään neljä ovat suurempia kuin ruudun oma luku.

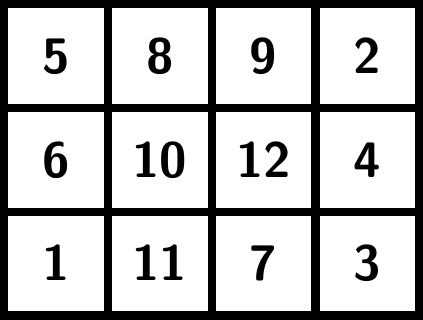
Lokaali lähestymistapa olisi tutkia jonkin pienen alueen lukuja ja tapauskäsittelyllä todistaa, että sieltä löytyy halutunlainen ruutu. Tämä vaatii paljon tapauskäsittelyä: esimerkiksi seuraavassa \(3 \times 4\) -ruudukossa yhdelläkään luvulla ei ole haluttua ominaisuutta, eli tutkittavan alueen pitää olla suurempi (ja tapauksia olisi siten hyvin monta).

Väite ei päde \(3 \times 4\) -ruudukossa.

Globaali lähestymistapa on ovelampi. Oletetaan, että väite ei päde. Täten jokaisella ruudulla on enintään kolme naapuria, joissa on sitä suurempia lukuja.

Toisaalta ruuduilla on (ruudukon reunoja lukuun ottamatta) kahdeksan naapuria, joten voisi kuvitella, että ruuduilla on keskimäärin neljä naapuria, joissa on suurempi luku.

Nämä ehdot eivät tunnu yhteensopivilta. Tämän saa formalisoitua laskemalla asioita. Piirretään ruudusta \(A\) nuoli sen naapuriruutuun \(B\), jos ruudun \(A\) luku on pienempi kuin ruudun \(B\). Tiedämme oletuksen nojalla, että jokaisesta ruudusta lähtee enintään kolme nuolta, eli nuolia on enintään \(3 \cdot 100 \cdot 100\).

Toisaalta nuolia on paljon, koska jokaisen kahden naapuriruudun välillä on nuoli. Pystysuunnassa olevia nuolia on \(99\) per pystyrivi eli yhteensä \(99 \cdot 100\). Vaakasuunnassa nuolia on sama määrä. Molempiin kahdesta eri vinosuunnasta osoittaa \[\begin{eqnarray} & & 1 + 2 + 3 + \ldots + 98 + 99 + 98 + \ldots + 3 + 2 + 1 \\ &=& \frac{99 \cdot 100}{2} + \frac{98 \cdot 99}{2} = 99 \cdot 99 \end{eqnarray}\] nuolta. Nuolia on siis \[2 \cdot 99 \cdot 100 + 2 \cdot 99 \cdot 99 = 2 \cdot 199 \cdot 99 > 3 \cdot 100 \cdot 100,\] mikä on ristiriita.

Kommentti. Lokaalia lähestymistapaa voisi parannella tutkimalla ruudukon pienimmän luvun läheisiä ruutuja. Pienimmän luvun omaava ruutu kelpaa, jos se ei ole ruudukon nurkassa. Nurkkatapauksen ratkaiseminen tapauskäsittelyllä olisi kuitenkin edelleen työlästä.

Tehtävän menetelmä on esimerkki kahdella tavalla laskemisesta: arvioimme ruudukossa olevien nuolien määrää kahdella tavalla (”yksittäisten ruutujen näkökulmasta” ja ”pysty-, vaaka- ja vinorivien näkökulmasta”) ristiriidan saamiseksi. Kahdella tavalla laskeminen on selkeä esimerkki globaalista menetelmästä. Myös seuraavan tehtävän ratkaisussa lasketaan jokin suure luovalla tavalla.

Tehtävä 30.3 Verkossa on \(100\) solmua. Tiedetään, ettei verkosta löydy kolmea solmua, joista minkä tahansa kahden välillä on kaari. Kuinka monta kaarta verkossa voi enintään olla?

Tehtävä on vaikea, joten paljastetaan aluksi vastaus: maksimimäärä kaaria on \(50 \cdot 50 = 2500\) ja tämän saavuttaa verkko, jossa on \(50\) solmua toisella puolella ja \(50\) solmua toisella ja eri puolien solmut on yhdistetty toisiinsa kaarella. (Tämän voi keksiä tutkimalla pieniä tapauksia.)

Paras ratkaisu on jakaa solmut kahteen osaan ja yhdistää eri osien solmut toisiinsa.

Tehtävässä on annettu verkolle lokaali ominaisuus (minkä tahansa kolmen solmun välillä on enintään kaksi kaarta) ja tästä halutaan globaali ominaisuus (kaarien määrä on enintään \(2500\)). Lokaalit lähestymistavat, kuten ”yritetään osoittaa, että mistä tahansa solmusta lähtee enintään näin monta kaarta” eivät anna riittävän hyviä rajoja. Yritetään globaaleja ideoita.

Ensimmäisenä mieleen voisi tulla seuraava idea: Tutkitaan kaikkia \({100 \choose 3}\) kolmen solmun joukkoa. Jokaisessa niistä on enintään kaksi kaarta, eli yhteensä kaaria tulee enintään \(2{100 \choose 3}\). Jokainen kaari esiintyy \(98\) eri kolmiossa, eli sama kaari tulee laskettua \(98\) kertaa. Täten kaarien määrä on enintään \[\frac{2{100 \choose 3}}{98} = \frac{100 \cdot 99}{3} = 3300.\]

Tämä on liian huono raja. Mistä huonous johtuu? Ongelma on siinä, että kaikissa kolmen solmun joukoissa ei ole kahta kaarta. Esimerkiksi optimaalisesta ratkaisusta voidaan valita kolme solmua samalta puolelta. Näiden solmujen välillä ei ole yhtäkään kaarta.

Tästä syystä on järkevää käydä solmukolmikoiden sijasta läpi kaaria ja summata asioita niiden kautta.

Valitaan jokin kaari, joka yhdistää kaksi solmua \(A\) ja \(B\). Solmuilla \(A\) ja \(B\) ei ole yhteisiä naapureita annetusta ehdosta johtuen. Täten solmujen \(A\) ja \(B\) asteiden summa on enintään \(100\): muihin \(98\) solmuun lähtee solmuista \(A\) ja \(B\) enintään yksi kaari, ja lisäksi \(A\):n ja \(B\):n välillä oleva kaari kasvattaa asteiden summaa kahdella.

Täten \[\sum_{\text{v\"alill\"a } A-B \text{ on kaari}} \deg(A) + \deg(B) \le 100E,\] missä \(E\) on verkon kaarien määrä. Huomataan, että kullakin solmulla \(V\) termi \(\deg(V)\) esiintyy vasemman puolen summassa yhteensä \(\deg(V)\) kertaa, joten epäyhtälön voi kirjoittaa muotoon \[\sum_{V \text{ on solmu}} \deg(V)^2 \le 100E.\] Tätä summaa saadaan arvioitua käyttämällä Epäyhtälöitä-tekstissä esitettyä QM-AM-epäyhtälöä: \[\sum_{V \text{ on solmu}} \deg(V)^2 \ge \frac{1}{100}\left(\sum_{\text{solmut } V} \deg(V)\right)^2 = \frac{1}{100}(2E)^2,\] missä käytettiin tietoa siitä, että asteiden summa on kaksi kertaa kaarien määrä. Täten \[\frac{1}{25}E^2 \le 100E,\] eli \(E \le 2500\).

Kommentti. On melko tyypillistä, että globaaleja argumentteja sovellettaessa tarvitaan arviointia ja epäyhtälöitä. Yllä oleva ratkaisu tarvitsi QM-AM-epäyhtälön, joka on klassinen epäyhtälö. Seuraavassa tehtävässä puolestaan tarvitaan karkeita arvioita.

Tehtävä 30.4 Turnauksessa jokainen pelaaja pelaa kaikkia muita pelaajia vastaan. Jokainen peli päättyy jommankumman pelaajan voittoon. Osoita, että on olemassa positiivinen kokonaisluku \(n\), jolla \(n\) pelaajan turnauksessa voi käydä seuraavasti:

Jos valitaan mitkä tahansa viisi turnauksen pelaajaa, on turnauksessa joku, joka on voittanut kunkin näistä viidestä pelaajasta.

Idea: Valitaan suuri \(n\) ja valitaan satunnainen turnaus. Tämä toimii.

Ratkaisu: Valitaan sellainen turnaus, jossa jokaisen pelin voittaja ratkaistaan heittämällä kolikkoa. Osoitetaan sitten, että haluttu ehto toteutuu suurella todennäköisyydellä (kun \(n\) on suuri). Tämä riittää: jos ei olisi yhtäkään halutunlaista turnausta, niin todennäköisyys onnistumiselle olisi nolla.

Valitaan jotkin viisi turnauksen pelaajaa. Millä todennäköisyydellä jokin tietty kuudes pelaaja voittaa heidät kaikki? Todennäköisyys tälle on \[\left(\frac{1}{2}\right)^5 = \frac{1}{32}.\] Todennäköisyys sille, ettei tämä kuudes pelaaja voita heitä kaikkia on siis \(31/32\). Täten todennäköisyys sille, ettei kukaan muu \(n-5\) pelaajasta voita kaikkia näistä viidestä pelaajasta on \[\left(\frac{31}{32}\right)^{n-5}.\] Oleellista on, että tämä todennäköisyys on hyvin lähellä nollaa (kyseessähän on eksponenttifunktio, jonka kantaluku on alle yksi).

Nyt todennäköisyys sille, että on olemassa vähintään yksi viiden pelaajan joukko, jolle halutunlaista kuudetta henkilöä ei löydy, on enintään \[{n \choose 5}\left(\frac{31}{32}\right)^{n-5},\] koska näitä viiden hengen joukkoja on \({n \choose 5}\).

Yllä oleva todennäköisyys on edelleen hyvin pieni (kun \(n\) on suuri): se on polynomi kertaa eksponenttifunktio, jonka kantaluku on alle yksi. Siis jos \(n\) on riittävän suuri, on kyseinen luku esimerkiksi alle \(50\%\). Tämä tarkoittaa, että \(n\) pelaajan satunnaisella turnauksella on yli \(50\) prosentin todennäköisyydellä haluttu ominaisuus, joten erityisesti näitä turnauksia on vähintään yksi.

Kommentti. Ratkaisun voi muotoilla myös ilman todennäköisyyksiä laskemalla (samanlaisilla ideoilla kuin yllä) yläraja kelpaamattomien turnausten määrälle ja toteamalla, että tämä on pienempi kuin kaikkien turnausten määrä. Ratkaisun idea on kuitenkin selkeämpi selittää todennäköisyyksien kautta.

Ratkaisun idealla on oma nimensäkin, ”probabilistinen metodi”. Menetelmällä voidaan ratkoa hyvin vaikeitakin ongelmia käyttämällä todennäköisyyslaskennan työkaluja.

Menetelmä on hyvin globaali. Mielenkiintoista on se, että menetelmällä voidaan todistaa jonkin asian (tässä tapauksessa tietynlaisen turnauksen) olemassaolo ilman, että oikeasti osataan konstruoida tällaista asiaa. Lokaalimpi lähestymistapa olisi konstruoida turnaus valikoimalla eri pelien lopputuloksia yksitellen. Tämä ei kuitenkaan käytännössä onnistu, koska pienillä \(n\) halutunlaista turnausta ei ole olemassa.

30.3 Tehtäviä

Tehtävien on tarkoitus demonstroida globaaleja menetelmiä. Voi olla lisäksi hyödyllistä miettiä, miltä lokaalit lähestymistavat näyttäisivät.

Tehtävä 1. Olkoon \(n\) positiivinen kokonaisluku, ja olkoon \(\sigma(n)\) luvun \(n\) tekijöiden summaa. (Esimerkiksi \(\sigma(6) = 1 + 2 + 3 + 6 = 11\).) Osoita, että \[\sigma(1) + \sigma(2) + \ldots + \sigma(n) \le n^2.\]

Tehtävä 2. Matematiikkakilpailussa on kuusi tehtävää ja \(200\) kilpailijaa. Kunkin kilpailutehtävän on ratkaissut vähintään \(120\) kilpailijaa. Osoita, että on olemassa sellaiset kaksi kilpailijaa, että kunkin tehtävän on ratkaissut vähintään toinen heistä.

Tehtävä 3. Olkoot \(a_1, \ldots , a_n\) reaalilukuja, missä \(n \ge 2\). Oletetaan, että \(a_1 + a_2 + \ldots + a_n = 0\) ja että kaikki luvuista eivät ole nollia. Osoita, että nämä luvut voidaan järjestää sellaiseksi lukujonoksi \(b_1, b_2, \ldots , b_n\), että \[b_1b_2 + b_2b_3 + \ldots + b_{n-1}b_n + b_nb_1 < 0.\]

Tehtävä 4. Osoita, että luvut \(1, 2, \ldots , 2000\) voidaan värittää kahdella värillä niin, ettei minkään \(18\) luvun pituisen aritmeettisen lukujonon kaikki luvut ole samanvärisiä.

Tehtävä 5. Osoita, että seuraava tilanne ei ole mahdollinen.

Juhlissa on henkilöitä, joista jotkut ovat ystäviä keskenään. (Ystävyys on molemminpuolista, eli jos \(A\) on \(B\):n ystävä, niin myös \(B\) on \(A\):n ystävä. Kukaan ei ole itsensä ystävä.) Kullakin henkilöllä on viisi ystävää ja kenellä tahansa kahdella henkilöllä on tasan kaksi yhteistä ystävää.