9 Laskennallinen kombinatoriikka
9.1 Johdanto
Laskennallisessa kombinatoriikassa nimensä mukaisesti lasketaan erilaisia kombinaatioiden eli yhdistelmien määriä. Tässä tekstissä esitetään muutama usein tarvittava perusidea sekä pari soveltavaa tehtävää.
9.2 Perusperiaatteet
Seuraavat ideat ovat hyvin yksinkertaisia, mutta koska niitä käytetään toistuvasti tästä eteenpäin, mainitaan ne selkeyden vuoksi. Käydään ideat läpi esimerkkien kautta.
Tuloperiaate. Jos ravintolassa on tarjolla kolmea eri alkuruokaa, viittä eri pääruokaa ja neljää eri jälkiruokaa, niin tilaamalla yhden alkuruoan, yhden pääruoan ja yhden jälkiruoan aterioita voidaan muodostaa \(3 \cdot 5 \cdot 4 = 60\) erilaista ateriaa.
Summaperiaate. Jos ravintolassa on kolme pöytää, joissa ensimmäisessä on \(6\) tuolia, toisessa \(4\) ja kolmannessa \(5\), on tuoleja yhteensä \(6+4+5 = 15\).
Tulo- ja summaperiaatteet yksinkertaisesti kertovat, että tiettyjen asioiden määrä saadaan tilanteesta riippuen kertomalla tai summaamalla yksittäisten vaihtoehtojen määrät.
9.3 Tärkeitä esimerkkejä
9.3.1 Esimerkki 1: Kertoma
Ajatellaan, että aluksi kortit otetaan käteen, ja kädestä kortteja laitetaan yksitellen pöydälle, ensimmäinen kortti rivin vasempaan päähän, toinen kortti sen oikealle puolelle, kolmas kortti sitä seuraavaksi ja niin edelleen. Ensimmäinen kortti voidaan valita \(8\) tavalla, koska kädessä on tällöin \(8\) korttia. Toisen kortin kohdalla kortteja on \(7\), joten vaihtoehtoja on \(7\). Seuraavilla korteilla vaihtoehtoja on \(6, 5, 4, 3, 2\) ja \(1\).
Tuloperiaatteen nojalla vastaus on \(8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1\), joka on \(40320\). Vaihtoehtoja on siis aika monta!
Yleisesti \(n\) kortilla vastaus on samaan tapaan \(n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot 3 \cdot 2 \cdot 1\). Tätä lukua merkitään \(n!\) ja kutsutaan luvun \(n\) kertomaksi (ei ”\(n\) huutomerkki”). Esimerkiksi \(8! = 40320\). Lukujen \(1, 2, 3, 4, 5, 6, 7, 8, 9, 10\) kertomat ovat1 \[1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800.\]
1 Lisäksi määritellään \(0! = 1\). Tämä voi aluksi tuntua omituiselta, mutta tälle on järkevät perustelut. Yksi perustelu: Jos summataan nolla lukua, on summa järkevä määritellä nollaksi. Jos nimittäin tutkimme esimerkiksi summaa \(1+2+3\) ja summaamme siihen vielä nolla lukua lisää, ei summan arvo muutu, joten nollan luvun summan tulee olla nolla. Vastaavasti jos kerromme nolla lukua keskenään, on tulo järkevä määritellä ykköseksi. Jos nimittäin tutkimme esimerkiksi tuloa \(1 \cdot 2 \cdot 3\) ja kerromme sitä vielä nollalla luvulla lisää, ei tulon arvo muutu, joten nollan luvun tulon tulee olla yksi.
Joidenkin asioiden (tämän tehtävän tapauksessa korttien) järjestystä kutsutaan permutaatioksi (voidaan siis sanoa, että \(8\) kortilla on \(40320\) eri permutaatiota).
9.3.2 Esimerkki 2: Binomikertoimet
Ensimmäinen täyte voidaan valita kahdeksalla eri tavalla. Toinen täyte puolestaan voidaan valita seitsemällä eri tavalla. Tuloperiaate antaisi siis, että vaihtoehtoja on \(8 \cdot 7 = 56\), mutta tämä ei ole aivan oikein. Täytteiden valitsemisen järjestyksellä ei tietenkään pitsaa tehdessä ole väliä, mutta tulemme yllä laskeneeksi jokaisen täyteparin kahteen kertaan. Nimittäin yksi tapa saada pitsaan täytteet A ja B on valita ensin täyte A ja sitten täyte B, ja toinen tapa on valita ensin täyte B ja sitten täyte A.
Tämän vuoksi vastaus tulee jakaa kahdella, eli oikea vastaus on \[\frac{8 \cdot 7}{2} = 28.\]
Samaan tapaan kuin yllä ensimmäinen veikkaus voisi olla \(8 \cdot 7 \cdot 6 \cdot 5 = 1680\), mutta tämä ei taaskaan ole aivan oikein. Tällä kertaa sama täyteyhdistelmä A, B, C, D voidaan valita \(4! = 24\) eri järjestyksessä (vertaa tehtävään 9.1). Tämän vuoksi veikkaus pitää jakaa luvulla \(4!\), eli oikea vastaus on \[\frac{8 \cdot 7 \cdot 6 \cdot 5}{24} = 70.\]
Yleisesti jos on \(n\) täytettä, joista voidaan valita jotkin \(k\), on vastaus tehtävään \[\frac{n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot (n - (k-1))}{k!}.\] Tätä lukua kutsutaan binomikertoimeksi, ja sitä merkitään \[{n \choose k}.\] (Tämä luetaan ”\(n\) yli \(k\)”.) Binomikertoimien kaavaa voi vielä hieman sieventää: huomataan, että \[\frac{n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot (n-(k-1))}{k!} = \frac{\frac{n!}{(n-k)!}}{k!} = \frac{n!}{k!(n-k)!},\] joten usein määritelmä kirjoitetaan muodossa \[{n \choose k} = \frac{n!}{k!(n-k)!}.\]
Huomaa, että \({n \choose 0} = 1\) ja \({n \choose n} = 1\): on tasan yksi pitsa, jossa ei ole täytteitä ja tasan yksi pitsa, jossa on kaikki \(n\) täytettä. Tässä on esimerkkejä binomikertomista:
\[{5 \choose 0} = 1, {5 \choose 1} = 5, {5 \choose 2} = 10, {5 \choose 3} = 10, {5 \choose 4} = 5, {5 \choose 5} = 1.\]
9.4 Lisää binomikertoimista
Binomikertoimilla on paljon käteviä ominaisuuksia. Käsitellään tässä joitain niistä.
Seuraavassa kolmiossa on binomikertoimia. Ylimmällä rivillä on binomikerroin \({0 \choose 0} = 1\), seuraavalla rivillä \({1 \choose 0}\) ja \({1 \choose 1}\), seuraavalla rivillä \({2 \choose 0}, {2 \choose 1}\) ja \({2 \choose 2}\) ja niin edelleen sopivasti aseteltuna.
| 1 | ||||||||||||
| 1 | 1 | |||||||||||
| 1 | 2 | 1 | ||||||||||
| 1 | 3 | 3 | 1 | |||||||||
| 1 | 4 | 6 | 4 | 1 | ||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 |
Kolmiota kutsutaan Pascalin kolmioksi. Kolmiosta huomataan seuraava asia: alempana oleva luku on sen kahden yläpuolella oleva luvun summa.
Todistus. Lauseen voi todistaa algebrallisesti käyttämällä määritelmää \({n \choose k} = n!/(k!(n-k)!)\) ja tekemällä laskuja. Tässä kuitenkin esitetään kombinatorinen todistus.
Mietitään, monellako tavalla \(n+1\) täytevaihtoehdosta voidaan valita \(k+1\) pitsatäytettä. Täyteyhdistelmien määrä on edellisen osion perusteella binomikerroin \({n+1 \choose k+1}\). Toisaalta yhdistelmät voi jakaa kahteen kategoriaan.
Kategoria 1. Täyte numero \(1\) tulee valituksi. Tällöin lopuista \(n\) täytteestä tulee valita vielä \(k\) täytettä. Tämä voidaan tehdä \({n \choose k}\) tavalla.
Kategoria 2. Täyte numero \(1\) ei tule valituksi. Tällöin lopuista \(n\) täytteestä tulee valita vielä \(k+1\) täytettä. Tämä voidaan tehdä \({n \choose k+1}\) tavalla.
Lauseen tulos seuraa summaperiaatteella.
9.5 Esimerkkitehtävä
Jos merkitsemme Annan saamien karkkien määrää \(a\):lla, Bellan \(b\):llä ja Caroliinan \(c\):llä, niin haluamme löytää yhtälön \[a + b + c = n\] ratkaisujen määrän, missä \(a, b\) ja \(c\) ovat kokonaislukuja ja vähintään \(0\).
On parikin tapaa, miten tehtävää voi lähestyä. Ensinnäkin voisi miettiä, miten ongelma toimii kahdella henkilöllä. Jos kahden henkilön, Danielin ja Emilin, tulee jakaa \(n\) karkkia keskenään, on vaihtoehtoja \(n+1\): Danielille voidaan antaa \(0, 1, 2, \ldots , n-1\) tai \(n\) karkkia ja loput annetaan Emilille.
Toiseksi voi tutkia, paljonko tapoja on pienillä \(n\):n arvoilla.
- Jos \(n = 0\), tapoja on vain \(1\) (kukaan ei saa mitään).
- Jos \(n = 1\), tapoja on \(3\) (valitaan, kenelle karkki annetaan).
- Jos \(n = 2\), tapoja on \(6\): on kolme tapaa, joissa joku saa molemmat karkit ja kolme tapaa, joissa jotkut kaksi saavat yhden karkin ja kolmas jää ilman.
- Jos \(n = 3\), tapoja on \(10\): joku voi saada kaikki kolme karkkia (\(3\) tapaa), joku saa kaksi karkkia ja joku toinen yhden (\(3 \cdot 2 = 6\) tapaa), kaikki saavat yhden karkin (\(1\) tapa).
Jotkut lukijat saattavat huomata, että tapojen määrät ovat \(1\), \(1+2\), \(1+2+3\), \(1+2+3+4\) ja niin edelleen. Tämä lukujono on tuttu Induktiivinen päättely -tekstistä, mikä vihjaa siihen, että vastaus tehtävään on \((n+1)(n+2)/2\). Tämän keksiminen voi auttaa tehtävän ratkaisussa.
Ensimmäistä lähestymistapaa voi soveltaa myös kolmelle henkilölle. Tutkitaan tapauksia sen mukaan, kuinka monta karkkia Annalle annetaan.
- Jos Annalle annetaan \(0\) karkkia, niin Bella ja Caroliina voivat jakaa \(n\) karkkia keskenään \(n+1\) tavalla.
- Jos Annalle annetaan \(1\) karkki, niin Bella ja Caroliina voivat jakaa \(n-1\) karkkia keskenään \(n\) tavalla.
- \(\vdots\)
- Jos Annalle annetaan \(n-1\) karkkia, niin Bella ja Caroliina voivat jakaa \(1\) karkin keskenään \(2\) tavalla
- Jos Annalle annetaan \(n\) karkkia, niin Bella ja Caroliina voivat jakaa \(0\) karkkia keskenään \(1\) tavalla.
Siis vastaus tehtävään on \(1 + 2 + 3 + \ldots + n + (n+1)\). Ja kuten Induktiivinen päättely -tekstissä laskettiin, tämä summa sievenee muotoon \((n+1)(n+2)/2\).)
Kommentti. Vastauksen \((n+1)(n+2)/2\) voi kirjoittaa binomikertoimena \({n+2 \choose 2}\). Alla esitetään myös ratkaisu, joka selittää luontevasti, miksi vastaus on tämä binomikerroin. (Ratkaisu on sen verran luova, että sitä olisi vaikea keksiä itse, minkä vuoksi yllä esitettiin lähestyttävämpi ratkaisu.)
Laitetaan Annan, Bellan ja Cellan \(n\) karkkia pöydälle riviin. Sijoitetaan riviin myöskaksi kapulaa, jotka jakavat karkit kolmeen ryhmään. Anna saa ensimmäisen kapulan vasemmalle puolelle jäävät karkit, Bella kapuloiden väliin jäävät karkit ja Cella kapuloiden oikealle puolelle jäävät karkit.
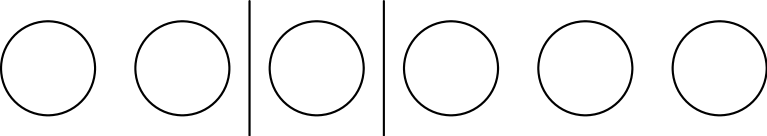
Monellako tavalla kapuloiden paikat voi valita? Voi ajatella, että joka tapauksessa rivissä tulee lopuksi olemaan \(n+2\) asiaa: \(n\) karkkia ja \(2\) kapulaa. Meidän tulee vain valita, mitkä näistä kahdesta paikasta ovat juuri kapuloiden paikat. Täten tapoja on \({n+2 \choose 2}\).
(Parasta menetelmässä on, että se toimii samaan tapaan myös useammalla kuin kolmella henkilöllä.)
9.6 Tehtäviä
Tehtävä 1. Pöydällä on palloja, jotka ovat joko punaisia, sinisiä tai punasinisiä. Tiedetään, että \(10\) pallossa on punaista, \(15\) pallossa on sinistä ja \(7\) pallossa on sekä punaista että sinistä. Montako palloja on yhteensä?
Tehtävä 2. Säännöllisen yhdeksänkulmion kärkipisteistä valitaan jotkin kolme. Kuinka monta eri tasakylkistä kolmiota näin voidaan muodostaa?
Tehtävä 3. \(6 \times 6\) -ruudukkoon laitetaan \(6\) pelimerkkiä niin, etteivät mitkään kaksi pelimerkkiä ole samalla pysty- tai vaakarivillä. Kuinka monella tavalla pelimerkit voidaan laittaa ruudukkoon?
Tehtävä 4. Pöydällä on rivissä neljä korttia, joissa on luvut yhdestä neljään. Kuinka monella tavalla kortit voi sekoittaa ja laittaa uudestaan riviin niin, ettei mikään kortti ole alkuperäisellä paikallaan?
Tehtävä 5. Pitsaan voidaan valita täytteitä \(n\) eri vaihtoehdosta. Pitsaan saa valita niin monta täytettä kuin haluaa (mukaan lukien \(0\) tai \(n\) täytettä), mutta samaa täytettä ei saa valita montaa kertaa. Osoita, että täyteyhdistelmien määrä on \(2^n\).
Tehtävä 6. Opettaja laittaa luokkansa \(9\) oppilasta istumaan kolmen eri pöydän ääreen. Ensimmäisen pöydän ääreen mahtuu \(4\) oppilasta, toisen ääreen \(3\) ja kolmannen ääreen \(2\). Kuinka monella eri tavalla opettaja voi jakaa oppilaat?
Tehtävä 7. Osoita, että Pascalin kolmion \(n\):nnen rivin lukujen summa on \(2^n\), kun laskeminen tehdään niin, että ylin rivi on nollas rivi. Toisin sanoen osoita, että \[{n \choose 0} + {n \choose 1} + \ldots + {n \choose n} = 2^n.\]
Tehtävä 8. Olkoot \(n\) ja \(0 \le k \le n\) kokonaislukuja. Tutkitaan lauseketta, joka saadaan kertomalla \((x+y)^n\) auki. Osoita, että termin \(x^ky^{n-k}\) kerroin lausekkeessa on \({n \choose k}\).
(Tätä tulosta kutsutaan binomilauseeksi ja se selittää, miksi lukuja \({n \choose k}\) kutsutaan binomikertoimiksi: ne vastaavat kertoimia polynomissa, joka saadaan kun binomi \((x+y)^n\) kerrotaan auki.)