21  Kiinalainen jäännöslause

Tekijä

Olli Järviniemi

21.1 Johdanto

Kiinalainen jäännöslause liittyy seuraavanlaiseen ideaan: ”luvun parillisuus ei kerro mitään sen jakojäännöksestä kolmella jaettaessa”. Tässä tekstissä esitetään lause, annetaan todistus ja demonstroidaan lauseen hyödyllisyyttä esimerkkien kautta.

21.2 Kiinalainen jäännöslause

Tehtävä 21.1 Oletetaan, että kokonaisluku \(x\) toteuttaa yhtälön \(x \equiv 1 \pmod{3}\). Mitä arvoja \(x\) voi saada modulo \(5\)?

Tutkitaan pieniä \(x\):n arvoja, joilla \(x \equiv 1 \pmod{3}\).

  • \(x = 1\): Tällöin \(x \equiv 1 \pmod{5}\)
  • \(x = 4\): Tällöin \(x \equiv 4 \pmod{5}\)
  • \(x = 7\): Tällöin \(x \equiv 2 \pmod{5}\)
  • \(x = 10\): Tällöin \(x \equiv 0 \pmod{5}\)
  • \(x = 13\): Tällöin \(x \equiv 3 \pmod{5}\)
  • \(x = 16\): Tällöin \(x \equiv 1 \pmod{5}\)
  • \(x = 19\): Tällöin \(x \equiv 4 \pmod{5}\)

Teemme kaksi huomiota:

  • Luku \(x\) saa kaikki mahdolliset arvot modulo \(5\). Siis tieto siitä, mitä \(x\) on modulo \(3\) ei kerro mitään siitä, mitä \(x\) on modulo \(5\).
  • Samat arvot toistuvat \(15\):n välein: \(x = 1\) ja \(x = 16\) antavat samat jakojäännökset kolmella ja viidellä jaettaessa, kuten myös \(x = 4\) ja \(x = 19\).

Kiinalainen jäännöslause kertoo juuri tästä ilmiöstä.

Lause 21.1 (Kiinalainen jäännöslause) Olkoot \(m_1, \ldots , m_k\) positiivisia kokonaislukuja. Oletetaan, että luvut \(m_i\) ovat pareittain yhteistekijättömiä, eli että \(\text{syt}(m_i, m_j) = 1\) kaikilla \(i \neq j\). Olkoot \(a_1, \ldots , a_k\) mielivaltaisia kokonaislukuja. Tällöin on olemassa sellainen kokonaisluku \(x\), että \[ \begin{cases} x \equiv a_1 \pmod{m_1} \\ x \equiv a_2 \pmod{m_2} \\ \vdots \\ x \equiv a_k \pmod{m_k}. \end{cases} \] Lisäksi tämä \(x\) on yksikäsitteinen modulo \(m_1m_2 \cdots m_k\).

Toisin sanoen tiedot siitä, mitä \(x\) on modulo \(m_1, m_2, \ldots\) ja \(m_k\), voidaan yhdistää tiedoksi siitä, mitä \(x\) on modulo \(m_1 \cdots m_k\).

Lauseessa tehdään oletus siitä, ettei luvuilla \(m_i\) ole yhteisiä tekijöitä. Tämä oletus on tietysti tarpeen: esimerkiksi luvun arvo modulo \(4\) kertoo jotakin luvun arvosta modulo \(6\), koska arvo modulo \(4\) kertoo luvun parillisuuden, mikä puolestaan näkyy arvossa modulo \(6\).

21.3 Kiinalaisen jäännöslauseen todistus

Kiinalaista jäännöslausetta voi visualisoida lukupyörien kautta, joista ensimmäisessä on \(m_1\) lukua, toisessa \(m_2\) ja niin edelleen. Alla on esitetty lukupyörät tapauksessa \(m_1 = 3, m_2 = 5, m_3 = 7\).

Kuva 21.1: Lukupyörät tapauksessa \(m_1 = 3, m_2 = 5, m_3 = 7\).

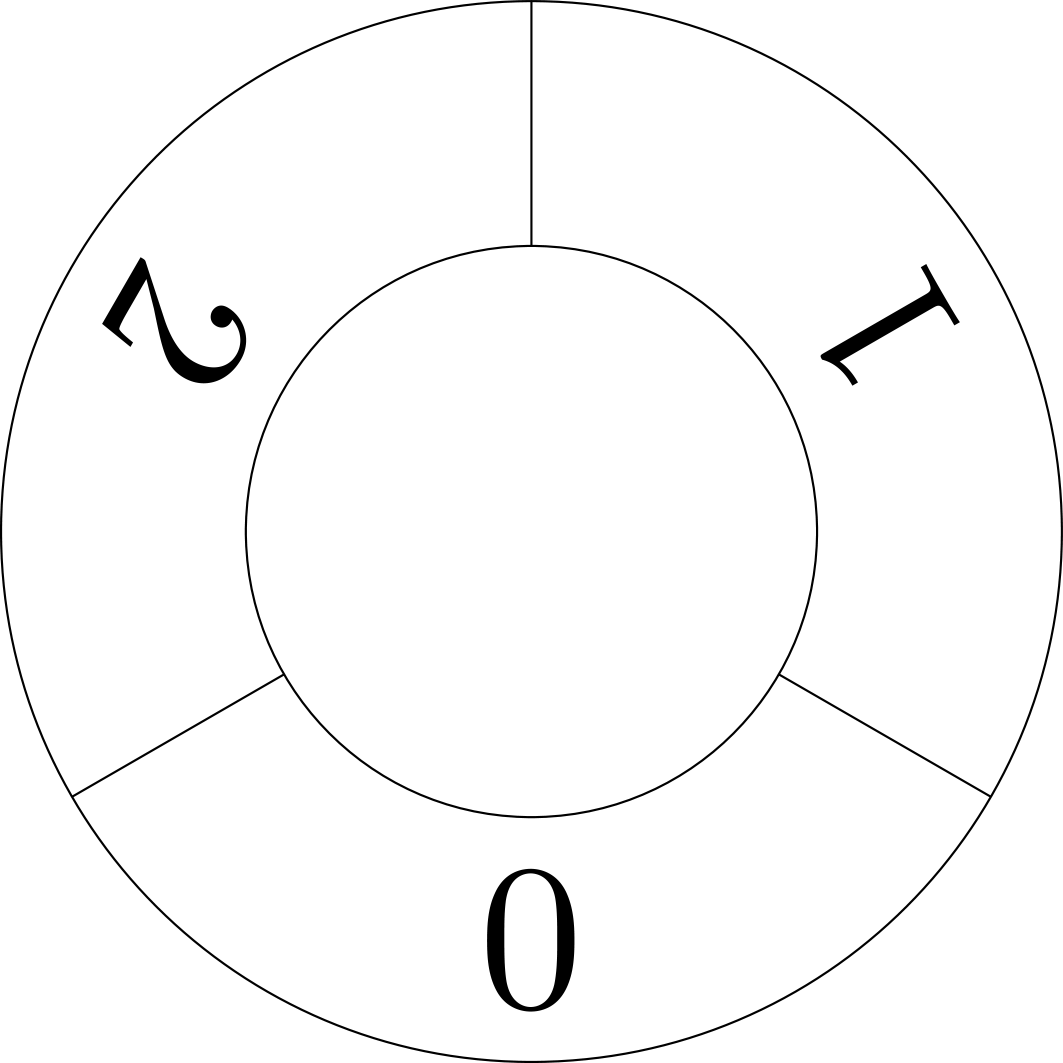
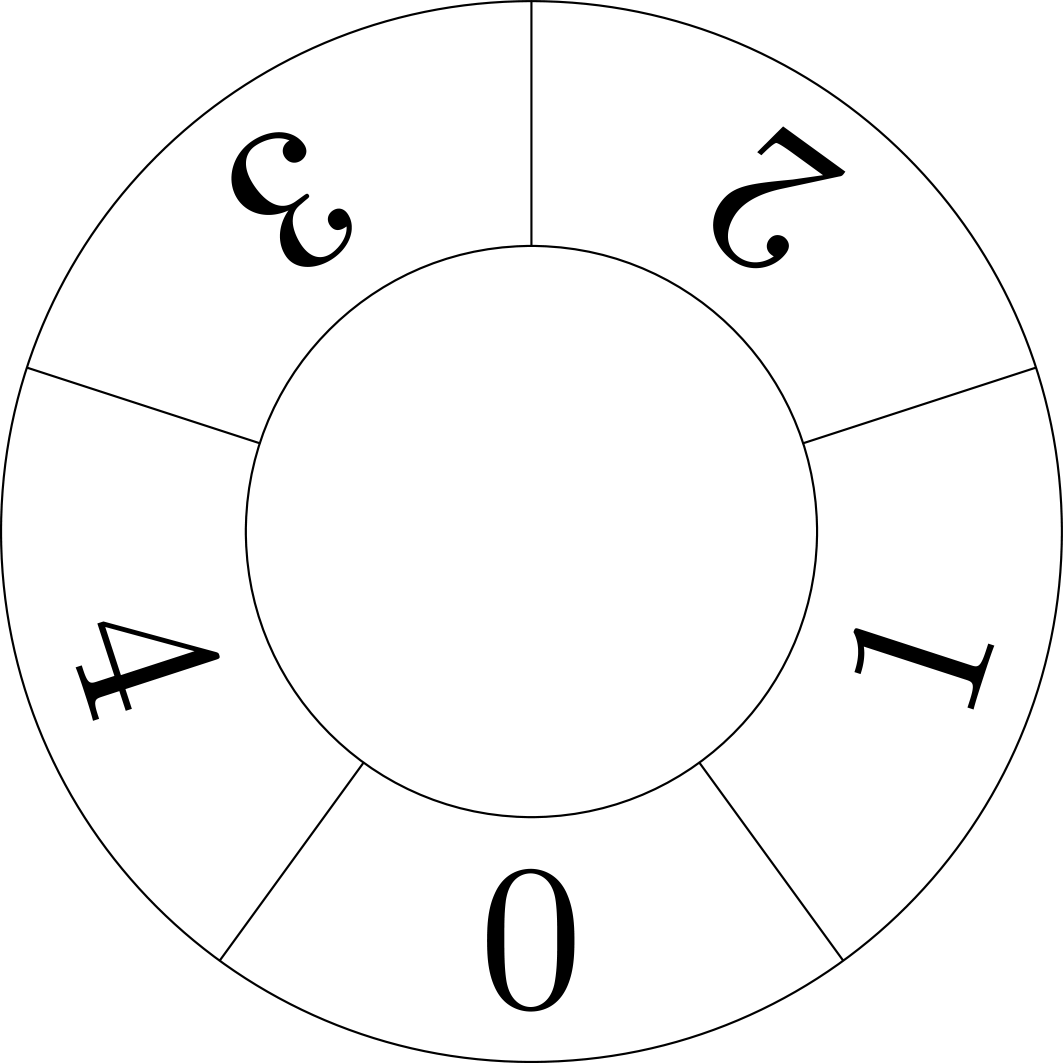
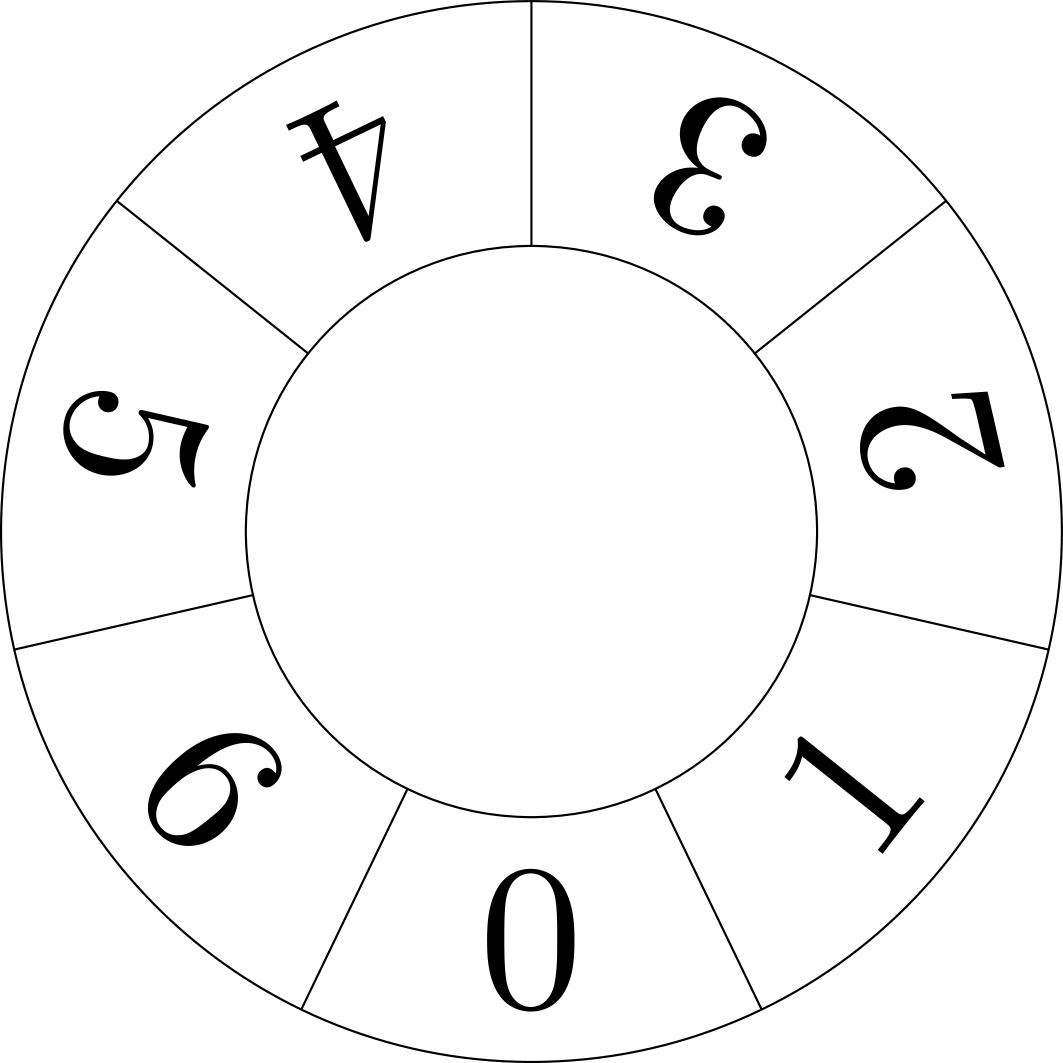
Kullekin kokonaisluvulle \(x\) pyörät voidaan asettaa sellaiseen asentoon, joka kertoo luvun \(x\) jakojäännökset luvuilla \(m_1, \ldots , m_k\) jaettaessa. Kuva 1 näyttää asennon, joka vastaa lukua \(x = 0\).

Kun lukua \(x\) kasvattaa yhdellä, kutakin pyörää pyöritetään yksi askel eteenpäin. Lukua \(x\) kasvatettaessa pyörien asennot muodostavat erilaisia yhdistelmiä. Esimerkiksi \(37\) askeleen jälkeen pyörät asettuvat seuraavaan asemaan, kertoen luvun \(x = 37\) jakojäännökset luvuilla \(m_i\) jaettaessa.

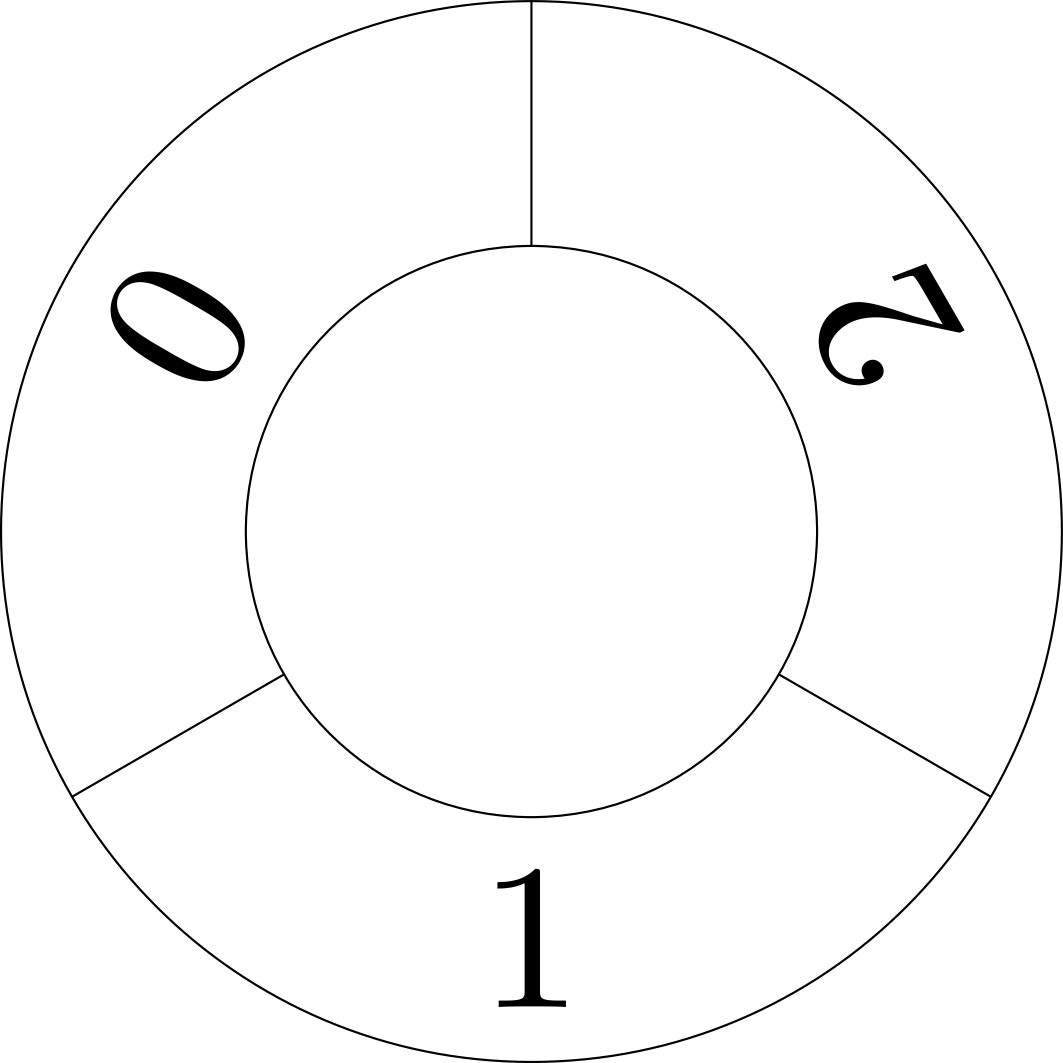
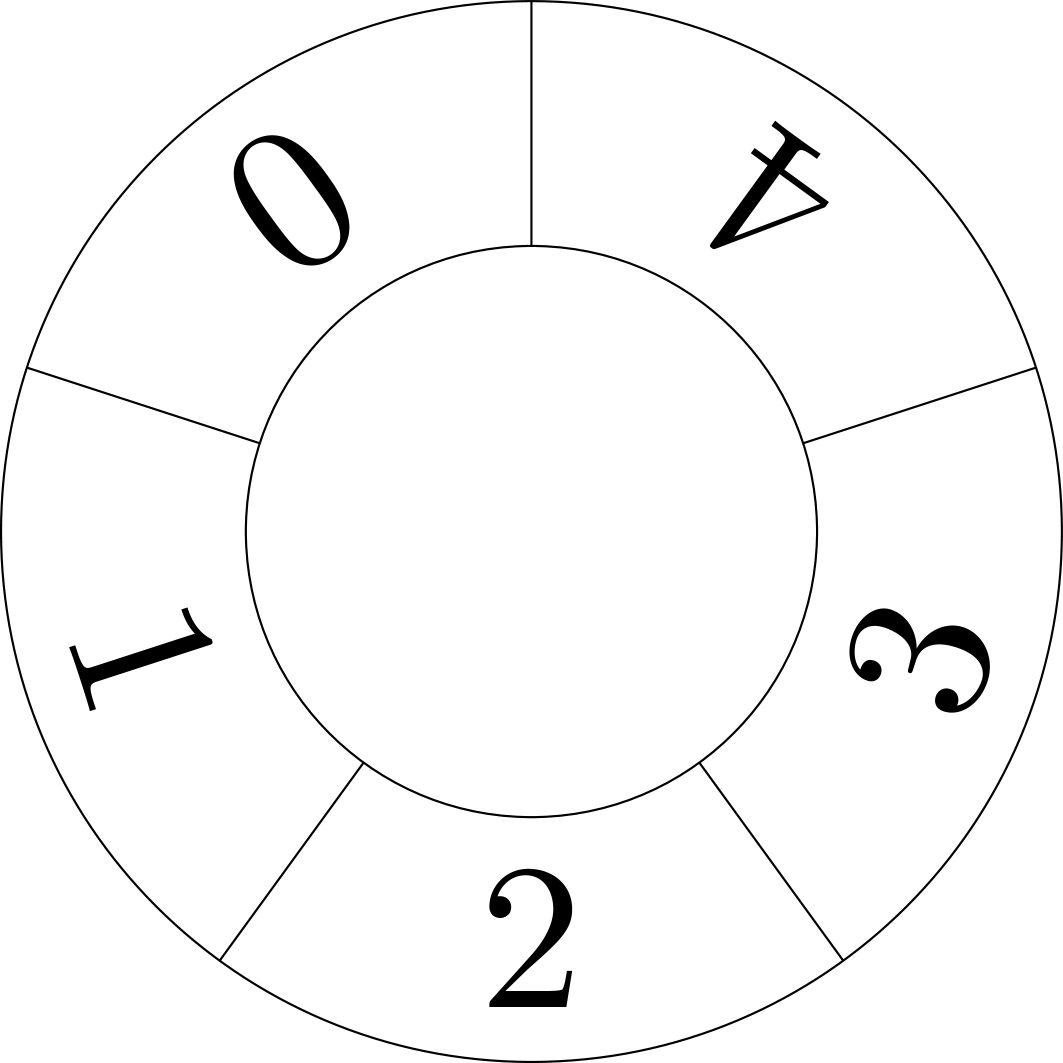
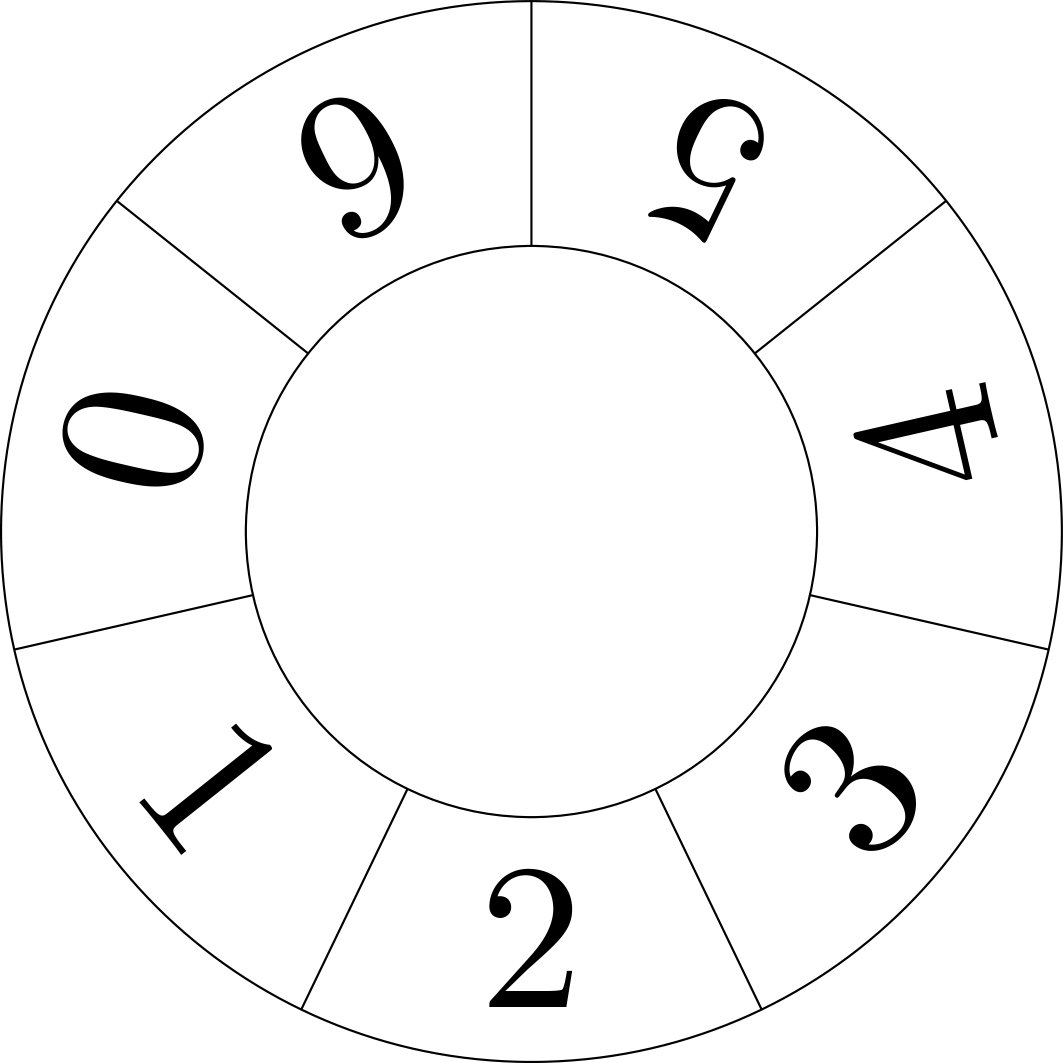
Kuva 21.2: Lukupyörät, kun kutakin on pyöräytetty \(37\) kertaa eteenpäin kuvan 21.1 tilanteesta.

Pyörien asennot kertovat, että \(37 \equiv 1 \pmod{3}\), \(37 \equiv 2 \pmod{5}\) ja \(37 \equiv 2 \pmod{7}\).

Kiinalainen jäännöslause väittää, että kaikki pyörien asentojen yhdistelmät ovat mahdollisia ja että samat yhdistelmät toistuvat tasan \(m_1 \cdots m_k\) askeleen välein.

Todistetaan lause. Teemme tämän kahdessa osassa. Ensin mietimme, kuinka usein sama asento voi esiintyä, minkä jälkeen osoitamme, että jokainen asento todella esiintyy.

Asentojen toistuminen. Kuinka usein sama pyörien asentojen yhdistelmä voi esiintyä? Mietitään vaikkapa kuvan 2 tilannetta. Kuinka monta askelta pitää mennä eteenpäin, jotta päädymme taas tilanteeseen, jossa ensimmäisessä pyörässä on luku \(1\), toisessa \(2\) ja kolmannessa \(2\)? Vastaus: \(3 \cdot 5 \cdot 7 = 105\) askelta. Alla perustelu (yleisessä tapauksessa).

Kuvitellaan, että lähdemme lukua \(x\) vastaavasta yhdistelmästä ja suorittamalla \(T\) askelta päädymme samaan tilanteeseen. Tämä tarkoittaa, että \[ \begin{aligned} x + T & \equiv x \pmod{m_1} \\ x + T & \equiv x \pmod{m_2} \\ & \vdots \\ x + T & \equiv x \pmod{m_k}. \end{aligned} \] Tästä seuraa, että \(T \equiv 0 \pmod{m_1}, T \equiv 0 \pmod{m_2}, \ldots , T \equiv 0 \pmod{m_k}\). Siis \(T\) on jaollinen kullakin luvuista \(m_1, m_2, \ldots , m_k\). Koska oletimme lukujen \(m_i\) olevan pareittain yhteistekijättömiä, saadaan tästä \[m_1m_2 \cdots m_k \mid T.\]

Toisaalta on selvää, että sama asentojen yhdistelmä toistuu \(m_1 \cdots m_k\) askeleen välein. Siis sama tilanne toistuu vain ja ainoastaan \(m_1 \cdots m_k\) askeleen välein.

Kaikkien asentojen esiintyminen. Mietitään lukuja \(x = 0, 1, \ldots , m_1m_2 \cdots m_k - 1\). Kutakin näistä luvuista vastaa jokin pyörien asentojen yhdistelmä.

Todistuksen ensimmäisen osan nojalla millään kahdella näistä luvuista ei ole samaa yhdistelmää. Koska tutkittavia lukuja on \(m_1m_2 \cdots m_k\) kappaletta ja pyörien mahdollisia asentoja on \(m_1m_2 \cdots m_k\) kappaletta, vastaa jokaista asentoa täsmälleen yksi luku. Siis jokainen yhdistelmä todella esiintyy, ja todistus on valmis.

21.4 Sovelluksia

Alla esitetään kolme erilaista sovelluskohdetta kiinalaiselle jäännöslauseelle. Ensimmäisen teema on konstruktio: haluamme löytää tietynlaisen kokonaisluvun, ja kiinalainen jäännöslause todistaa sellaisen olemassaolon. Toisen teema on yhdistäminen: eri moduloilla saatavia tietoja voi yhdistellä. Kolmannen teema on hajottaminen: isompi ongelma voidaan kiinalaisen jäännöslauseen avulla hajottaa pienempiin ongelmiin, jotka osataan ratkaista.

Tehtävä 21.2 Osoita, että on olemassa jotkin \(100\) peräkkäistä positiivista kokonaislukua, joista kullakin on vähintään \(100\) tekijää.

Haluamme siis löytää positiivisen kokonaisluvun \(x\), jolla kullakin luvuista \(x, x+1, \ldots , x+99\) on vähintään \(100\) tekijää. Meillä on melko paljon valinnanvaraa: muuta ei vaadita kuin että kullakin luvuista \(x+i\) on paljon tekijöitä, mutta saamme itse päättää, mitä nämä tekijät ovat.

Valitaan jotkin positiiviset kokonaisluvut \(m_1, \ldots , m_{100}\) ja yritetään valita \(x\) niin, että \(x\) on jaollinen luvulla \(m_1\), \(x+1\) luvulla \(m_2\) ja niin edelleen. Tämä voidaan muotoilla kongruenssien kautta muodossa \[ \begin{cases} x & \equiv 0 \pmod{m_1} \\ x + 1 & \equiv 0 \pmod{m_2} \\ \vdots \\ x + 99 & \equiv 0 \pmod{m_{100}}. \end{cases} \] Mitä ehtoja haluamme lukujen \(m_i\) toteuttavan? Ensinnäkin haluamme, että kullakin niistä on vähintään \(100\) tekijää, jotta tehtävä ratkeaa. Toiseksi luvut \(m_i\) kannata valita olemaan pareittain yhteistekijättömiä, jotta pääsemme käyttämään kiinalaista jäännöslausetta. Molemmat näistä valinnoista voidaan toteuttaa. Voidaan valita vaikka \(m_1\) olemaan ensimmäisen sadan alkuluvun tulo, \(m_2\) olemaan seuraavan sadan alkuluvun tulo ja niin edelleen. Nyt yllä olevalla yhtälöryhmällä on kiinalaisen jäännöslauseen nojalla ratkaisu: yhtälöryhmähän voidaan kirjoittaa muodossa \[ \begin{cases} x \equiv 0 \pmod{m_1} \\ x \equiv -1 \pmod{m_2} \\ \vdots \\ x \equiv -99 \pmod{m_{100}} \end{cases} \] Tämä ratkaisu \(x\) toteuttaa tehtävänannon ehdon (kunhan vain valitaan \(x\) olemaan positiivinen, mikä voidaan tehdä).

Tehtävä 21.3 Polynomin \(P\) kertoimet ovat kokonaislukuja. Tiedetään, että on olemassa kokonaisluku \(a\), jolla \(P(a)\) on jaollinen kymmenellä. Tiedetään myös, että on olemassa kokonaisluku \(b\), jolla \(P(b)\) on jaollinen seitsemällä. Osoita, että on olemassa kokonaisluku \(c\), jolla \(P(c)\) on jaollinen luvulla \(70\).

Haluamme yhdistää lukujen \(a\) ja \(b\) ne ominaisuudet, joiden ansiosta \(P(a)\) ja \(P(b)\) ovat jaollisia kymmenellä ja seitsemällä. Tämä onnistuu kohtalaisen helposti: kiinalaisen jäännöslauseen nojalla on olemassa kokonaisluku \(c\), jolla \[ \begin{cases} c \equiv a \pmod{10} \\ c \equiv b \pmod{7}. \end{cases} \] Ensimmäisen yhtälön ja kongruenssien perusominaisuuksien nojalla nyt pätee \(P(c) \equiv P(a) \pmod{10}\). Oletuksen nojalla \(P(a) \equiv 0 \pmod{10}\), joten \(P(c)\) on jaollinen kymmenellä. Vastaavasti \(P(c) \equiv P(b) \equiv 0 \pmod{7}\), joten \(P(c)\) on jaollinen seitsemällä. Täten \(P(c)\) on jaollinen myös luvulla \(10 \cdot 7 = 70\).

Tehtävä 21.4 Onko olemassa kokonaislukua \(x\), jolla \(x^2 + 1\) on jaollinen luvulla \(650\)?

Voisimme periaatteessa käydä kaikki luvut modulo \(650\) läpi ja katsoa, saadaanko ratkaisua. On kuitenkin paljon tehokkaampi tapa.

Huomataan, että luvun \(650\) alkutekijähajotelma on \[650 = 2 \cdot 5^2 \cdot 13.\] On luontevaa tutkia, voiko \(x^2 + 1\) olla jaollinen luvuilla \(2, 5^2\) ja \(13\) erikseen. Jos on, niin nämä jaollisuusehdot voidaan yhdistää samaan tapaan kuin edellisessä tehtävässä. Olemme siis saaneet hajotettua tehtävän pienempiin tapauksiin.

Käsitellään nämä pienemmät tapaukset. Yhtälöllä \(x^2 + 1 \equiv 0 \pmod{2}\) on ratkaisu \[x \equiv 1 \pmod{2}.\] Yhtälön \(x^2 + 1 \equiv 0 \pmod{5^2}\) tapauksessa voitaisiin käydä kaikki \(25\) vaihtoehtoa läpi. Hakua saa hieman nopeutettua huomaamalla, että yhtälöllä \(x^2 + 1 \equiv 0 \pmod{5}\) on ratkaisut \(x \equiv 2 \pmod{5}\) ja \(x \equiv 3 \pmod{5}\), joten myös modulo \(5^2\) ratkaisun tulee olla \(2\) tai \(3\) modulo \(5\). Jäljelle jää vain \(10\) vaihtoehtoa, ja löydetään ratkaisu \[x \equiv 7 \pmod{25}.\] (Myös \(x \equiv 18 \pmod{25}\) kävisi.) Modulo \(13\) löydetään \[x \equiv 5 \pmod{13}.\] (Myös \(x \equiv 8 \pmod{13}\) kävisi.)

Eli jokaiselle yksittäiselle alkuluvun potenssille löytyi ratkaisu. Kiinalaisen jäännöslauseen nojalla yhtälöryhmällä \[ \begin{cases} x \equiv 1 \pmod{2} \\ x \equiv 7 \pmod{25} \\ x \equiv 5 \pmod{13} \end{cases} \] on ratkaisu. Tällä ratkaisulla pätee \(x^2 + 1 \equiv 0 \pmod{650}\), eli vastaus tehtävään on kyllä.

21.5 Tehtäviä

Tehtävä 1. Ratkaise yhtälöpari \(x \equiv 3 \pmod{5}\), \(x \equiv 2 \pmod{7}\).

Tehtävä 2. Ratkaise yhtälöryhmä \[ \begin{cases} x \equiv 1 \pmod{2} \\ x \equiv 2 \pmod{3} \\ x \equiv 3 \pmod{5} \\ x \equiv 4 \pmod{7}. \end{cases} \]

Tehtävä 3. Osoita, että on olemassa miljoona peräkkäistä positiivista kokonaislukua, joista mikään ei ole alkuluku.

Tehtävä 4. Olkoot \(x\) ja \(y\) kokonaislukuja. Sanotaan, että koordinaatiston piste \((x, y)\) näkyy origosta, jos pisteiden \((0, 0)\) ja \((x, y)\) välisellä janalla ei ole muita pisteitä, joiden molemmat koordinaatit ovat kokonaislukuja. Osoita, että on olemassa \(100 \times 100\) -neliö, jonka mikään kokonaislukupiste ei näy origosta.

Tehtävä 5. Olkoot \(n\) ja \(m\) positiivisia kokonaislukuja, ja olkoon \(d = \text{syt}(n, m)\). Osoita, että yhtälöparilla \[ \begin{cases} x \equiv a \pmod{n} \\ x \equiv b \pmod{m} \end{cases} \] on kokonaislukuratkaisuja \(x\) jos ja vain jos \(a \equiv b \pmod{d}\), ja osoita, että ratkaisut ovat yksikäsitteisiä modulo \(\text{pyj}(n, m)\).