19  Summia

Tekijä

Olli Järviniemi

19.1 Johdanto

Tässä tekstissä käsitellään erilaisten summien laskemista, kuten \[1 + 2 + 3 + \ldots + n,\] \[1 + 2 + 4 + \ldots + 2^n\] ja \[1^2 + 2^2 + 3^2 + \ldots + n^2.\]

19.2 Summanotaatio

Aluksi esitetään tiivis tapa esittää summia. Merkintä näyttää tältä: \[\sum_{i = 1}^{100} 3i - 1.\] Tässä vasemmalla puolella oleva \(\Sigma\)-merkki (kreikan kielen kirjain sigma) kuvastaa summaamista. Alhaalla oleva merkintä \(i = 1\) kertoo, että aloitamme summaamisen ykkösestä ja ylhäällä oleva \(100\) kertoo, että lopetamme summaamisen sadan kohdalla. Lauseke \(3i - 1\) kertoo, mitä oikeastaan summataan. Lausekkeen arvot ovat \(2, 5, 8, 11, \ldots , 299\), kun \(i\) käy läpi luvut \(i = 1, 2, 3, \ldots , 100\). Yllä oleva summa tarkoittaa siis samaa kuin \[2 + 5 + 8 + 11 + \ldots + 299.\]

Tässä on muita esimerkkejä: \[\sum_{i = 1}^{100} i = 1 + 2 + 3 + \ldots + 100,\] \[\sum_{i = 1}^{100} 2^{i-1} = 2^0 + 2^1 + 2^2 + \ldots + 2^{99}.\] Summan alku- ja loppupisteet voivat myös olla muuttujia ja summattavan muuttujan ei tarvitse olla \(i\). Esimerkiksi \[\sum_{k = 1}^n k = 1 + 2 + 3 + \ldots + n.\]

19.3 Tärkeä perussumma

Ehkäpä tärkein tämän tekstin summista on summa \[1 + 2 + 3 + \ldots + n.\] Tätä käsitellään tässä osiossa. (Summaa on käsitelty tärkeytensä vuoksi myös Induktiivinen päättely -tekstissä.)

Tehtävä 19.1 Laske \(1 + 2 + 3 + \ldots + 100\).

Ratkaisu 1. Summassa on \(100\) termiä. Keskimäärin ne ovat noin \(50\), eli summan arvo on noin \(5000\). Tarkemmin huomataan, että keskimäärin luvut ovat \(50{,}5\), koska luvut voidaan jakaa pareihin \[(1, 100), (2, 99), (3, 98), \ldots , (50, 51),\] joissa kunkin parin lukujen keskiarvo on \(50\text{,}5\). Täten haluttu summa on \[100 \cdot 50{,}5 = 5050.\]

Ratkaisu 2. Summan voi ajatella visuaalisesti erään portaikon ruutujen määränä. Alla on esitetty summa \(1 + 2 + 3 + \ldots + 7\) portaikkona.

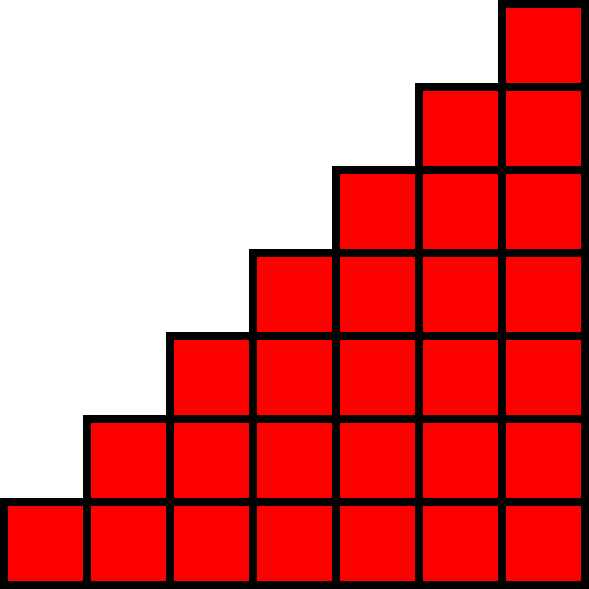
Summaa voi ajatella portaikon ruutujen määrän kautta.

Voimme tehdä portaikosta kopion ja asettaa kopion niin, että saamme suorakulmion:

Summa \(1 + 2 + \ldots + 7\) on puolet \(7 \times 8\) -suorakulmion pinta-alasta.

Tästä nähdään, että \[1 + 2 + 3 + \ldots + 7 = \frac{1}{2} \cdot 7 \cdot 8 = 28.\] Vastaavasti \[1 + 2 + 3 + \ldots + 100 = \frac{1}{2} \cdot 100 \cdot 101 = 5050.\] Tietysti samaan tapaan saadaan yleisesti \[1 + 2 + 3 + \ldots + n = \frac{n(n+1)}{2}.\]

19.4 Klassikkoesimerkki

Tehtävä 19.2 Laske \[\sum_{i = 1}^{100} \frac{1}{i(i+1)} = \frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \ldots + \frac{1}{100 \cdot 101}.\]

Ratkaisu 1 (induktiivinen ratkaisu). Tutkimalla pieniä tapauksia huomataan, että \[\frac{1}{1 \cdot 2} = \frac{1}{2},\] \[\frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} = \frac{1}{2} + \frac{1}{6} = \frac{2}{3},\] \[\frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \frac{1}{3 \cdot 4} = \frac{2}{3} + \frac{1}{12} = \frac{3}{4}\] ja \[\frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \frac{1}{3 \cdot 4} + \frac{1}{4 \cdot 5} = \frac{3}{4} + \frac{1}{20} = \frac{4}{5}.\] Kuvio on selvä, ja sen voi todistaa käyttämällä induktiivista päättelyä. Yksityiskohtia ei käydä läpi tässä.

Ratkaisu 2 (teleskooppisummaratkaisu). Huomataan1, että \[\frac{1}{i(i+1)} = \frac{1}{i} - \frac{1}{i+1}.\] (Tämän pätevyyden voi tarkistaa esimerkiksi kertomalla puolittain luvulla \(i(i+1)\) ja sieventämällä. Sitä, mistä tämän voi keksiä, käsitellään seuraavassa osiossa.) Täten \[\begin{eqnarray} & & \frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \frac{1}{3 \cdot 4} + \ldots + \frac{1}{100 \cdot 101} \\ &=& \left(\frac{1}{1} - \frac{1}{2}\right) + \left(\frac{1}{2} - \frac{1}{3}\right) + \left(\frac{1}{3} - \frac{1}{4}\right) + \ldots + \left(\frac{1}{100} - \frac{1}{101}\right) \\ &=& \frac{1}{1} - \frac{1}{101} = \frac{100}{101}, \end{eqnarray}\] koska summassa melkein kaikki supistuu pois.

  • 1 Lukiomatematiikkaa pitkälle opiskelleet saattavat huomata, että kyse on osamurtokehitelmästä.

    • Ratkaisun 2 ideaa kutsutaan teleskooppisummaksi. Ideana on siis kirjoittaa summan termit sellaiseen muotoon, että summattaessa termejä supistuu pois. Nimitys ”teleskooppisumma” tulee siitä, että summa kutistuu kasaan kuten teleskooppi.

    19.5 Teleskooppisummat

    Teleskooppisumma voi aluksi tuntua melko satunnaiselta tempulta, mutta sitä voi käyttää yllättävän monen summan laskemiseen. Alla on tästä esimerkkejä.

    Tehtävä 19.3 Laske \[\sum_{k = 0}^{n-1} 2^{k} = 1 + 2 + 4 + 8 + \ldots + 2^{n-1}.\]

    Idea: Yritetään kirjoittaa \(2^{k}\) muotoon \(f(k+1) - f(k)\). Jos tämä onnistuu, voimme laskea summan teleskooppisummana.

    Koska \(2^{k}\) on eksponenttifunktio, voisi veikata että \(f(k)\) kannattaa myös valita joksikin eksponenttilausekkeeksi. Veikataan \(f(k) = 2^k\). Tämä toimii: \[f(k+1) - f(k) = 2^{k+1} - 2^k = 2^k.\] Täten summan voi kirjoittaa muodossa

    \[\begin{eqnarray} & & 1 + 2 + 4 + 8 + \ldots + 2^{n-1} \\ &=& \left(2 - 1\right) + \left(4 - 2\right) + \left(8 - 4\right) + \ldots + \left(2^n - 2^{n-1}\right) \\ &=& 2^n - 1. \end{eqnarray}\] Haluttu summa on siis \(2^n - 1\).

    Tehtävä 19.4 Laske \[\sum_{k = 1}^n k^2 = 1^2 + 2^2 + 3^2 + \ldots + n^2.\]

    Idea: Yritetään kirjoittaa \(k^2\) muotoon \(f(k+1) - f(k)\), jolloin saamme jälleen teleskooppisumman.

    Mistä keksimme sellaisen lausekkeen \(f\), jolla \(f(k+1) - f(k) = k^2\)? Luonnollinen arvaus on, että \(f\) on polynomi, koska \(k^2\) on. Aluksi voisi veikata, että \(f\) on jokin toisen asteen polynomi \[f(i) = ak^2 + bk + c.\] Huomataan kuitenkin, että toisen asteen termit supistuvat pois, koska erotuksessa \[ f(k+1) - f(k) = \left(a(k+1)^2 + b(k+1) + c\right) - \left(ak^2 + bk + c\right) \] molemmissa erotuksen polynomeissa termin \(k^2\) kerroin on \(a\).

    Veikataan sitten, että \(f\) on jokin kolmannen asteen polynomi \[f(k) = ak^3 + bk^2 + ck + d.\] Lasketaan erotus. Tämä on hieman työlästä, mutta ei voi mitään.

    \[\begin{eqnarray} & & f(k+1) - f(k) \\ &=& \left(a(k+1)^3 + b(k+1)^2 + c(k+1) + d\right) - \left(ak^3 + bk^2 + ck + d\right) \\ &=& \left(a(k^3 + 3k^2 + 3k + 1) + b(k^2 + 2k + 1) + c(k+1) +d\right) - \left(ak^3 + bk^2 + ck + d\right) \\ &=& \left(ak^3 + (3a+b)k^2 + (3a + 2b + c)k + (a+b+c+d)\right) - \left(ak^3 + bk^2 + ck + d\right) \\ &=& 3ak^2 + (3a + 2b)k + (a+b+c). \end{eqnarray}\]

    Haluamme, että tämä on sama kuin \(k^2\). Täten tulee olla \[ \begin{cases} 3a = 1 \\ 3a + 2b = 0 \\ a + b + c = 0. \end{cases} \] Tämä on helppo yhtälöryhmä: ensimmäisestä yhtälöstä saadaan \(a = 1/3\) ja sen jälkeen toisesta \(b = -1/2\) ja kolmannesta \(c = 1/6\). Luku \(d\) voi olla mitä vain. Valitaan yksinkertaisuuden vuoksi \(d = 0\).

    Täten \[f(k) = \frac{1}{3}k^3 - \frac{1}{2}k^2 + \frac{1}{6}k.\] Nyt pääsemme käyttämään teleskooppisummaa: \[\begin{eqnarray} & & 1^2 + 2^2 + 3^2 + \ldots + n^2 \\ &=& \left(f(2) - f(1)\right) + \left(f(3) - f(2)\right) + \ldots + \left(f(n+1) - f(n)\right) \\ &=& f(n+1) - f(1). \end{eqnarray}\] Enää pitää laskea vastaus, mikä on jälleen hieman työlästä.

    \[\begin{eqnarray} & & f(n+1) - f(1) \\ &=& \left(\frac{1}{3}(n+1)^3 - \frac{1}{2}(n+1)^2 + \frac{1}{6}(n+1)\right) - \left(\frac{1}{3} - \frac{1}{2} + \frac{1}{6}\right) \\ &=& \frac{n^3 + 3n^2 + 3n + 1}{3} - \frac{n^2 + 2n + 1}{2} + \frac{n+1}{6} \\ &=& \frac{2(n^3 + 3n^2 + 3n + 1) - 3(n^2 + 2n + 1) + (n+1)}{6} \\ &=& \frac{2n^3 + 3n^2 + n}{6}. \end{eqnarray}\]

    Vastauksen voi kirjoittaa vielä hieman sievemmin tulomuotoon \[\frac{n(n+1)(2n+1)}{6}.\]

    Kommentti. Yleisesti käy niin, että jos erotuksen \(f(k+1) - f(k)\) halutaan olevan vaikkapa tietty viidennen asteen polynomi, niin oikea \(f\):n valinta on jokin kuudennen asteen polynomi.

    Jos taas halutaan, että \(f(k+1) - f(k)\) on jokin eksponenttifunktio \(a^k\) (missä \(a \neq 1\)), niin voidaan valita \(f(k)\) olemaan \(a^k\) kerrottuna sopivalla vakiolla: \[f(k) = \frac{a^k}{a-1}.\]

    (Lukiomatematiikkaa pitkälle opiskellut saattaa huomata menetelmissä joitakin yhteyksiä derivointiin ja integrointiin. Tästä voisi kirjoittaa kokonaan oman tekstinsä, mutta lyhyesti: Derivaatta määritellään raja-arvona lausekkeesta \((f(x+h) - f(x))/h\). Entä jos määrittelemme ”diskreetin derivaatan” kaavalla \(f^{\ast}(x) = f(x+1) - f(x)\), mikä vastaa arvoa \(h = 1\)? Funktion \(f\) ”diskreetti integraali” on sitten sellainen funktio \(F\), jolla \(F^{\ast}(x) = f(x)\) eli \(F(x+1) - F(x) = f(x)\). Siis teleskooppisumman metsästys vastaa ”diskreettiä integrointia”. Tässä valossa ei ole yllättävää, että polynomien ja eksponenttifunktioiden diskreetit integraalit ovat myös polynomeja ja eksponenttifunktioita – sama juttu nimittäin pätee myös tavallisilla, ”jatkuvilla” integraaleilla.)

    19.6 Tehtäviä

    Tehtävä 1. Kirjoita summa \[\sum_{k = 1}^n k = 1 + 2 + 3 + \ldots + n\] teleskooppisummana ja laske summa.

    Tehtävä 2. Laske \[\sum_{k = 1}^n 2k+1 = 1 + 3 + 5 + 7 + \ldots + (2n+1)\] teleskooppisummalla tai induktiivisella päättelyllä.

    Tehtävä 3. Laske \[\sum_{k = 0}^{n-1} 3^k = 1 + 3 + 9 + 27 + \ldots + 3^{n-1}.\]

    Tehtävä 4. Määritellään binomikerroinpolynomit2 \(P_0, P_1, P_2, P_3, \ldots\) kaavoilla

  • 2 Binomikertoimia on käsitelty Laskennallinen kombinatoriikka -tekstissä.

    • \[\begin{gather*} P_0(x) = 1, \quad P_1(x) = x, \\[1ex] P_2(x) = \frac{x(x-1)}{2!}, \quad P_3(x) = \frac{x(x-1)(x-2)}{3!} \end{gather*}\]

    ja yleisesti \[P_n(x) = \frac{x(x-1)(x-2) \cdots (x-(n-1))}{n!}.\]

    1. Osoita, että \[P_{n+1}(x+1) - P_{n+1}(x) = P_n(x),\] kun \(n \ge 0\).
    2. Etsi sellaiset luvut \(a\) ja \(b\), joilla \[x^2 = aP_2(x) + bP_1(x).\]
    3. Laske tätä kautta summa \[\sum_{x = 1}^n x^2 = 1^2 + 2^2 + \ldots + n^2.\]

    Tehtävä 5. Etsi sellainen lauseke \(f\), jolla \(f(k+1) - f(k) = k2^k\), ja laske summa \[\sum_{k = 1}^n k2^k.\]