25 Kertolasku kongruensseissa
25.1 Johdanto
Yhteenlasku kongruensseissa on hyvinkin selvä. Aloittamalla nollasta ja lisäämällä koko ajan ykköstä saadaan käytyä läpi kaikki luvut. Luvut muodostavat selkeän ringin tai syklin.
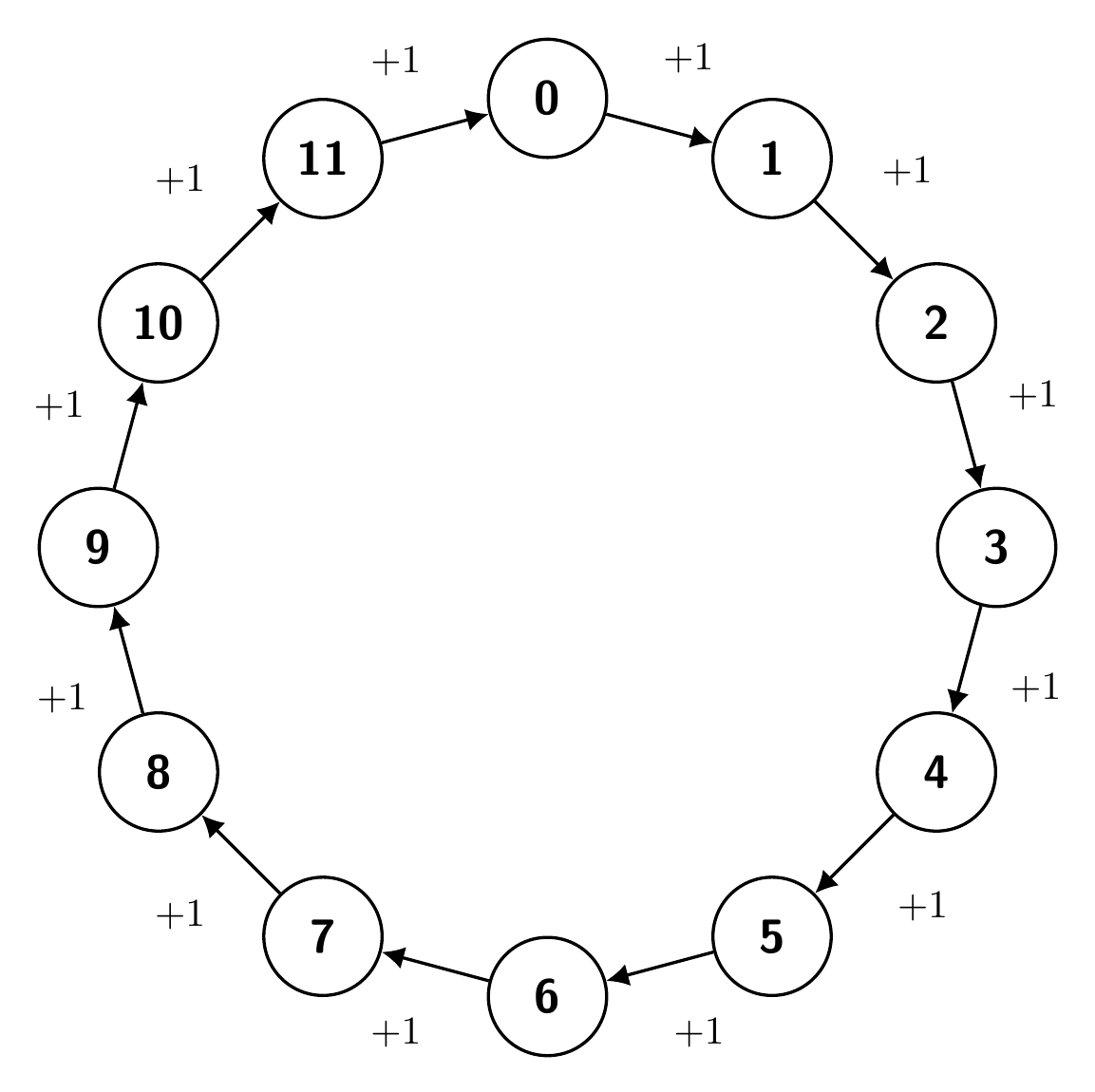
Kertolaskusta sen sijaan nähtiin aiemmassa tekstissä seuraava kuva.

Kertolasku tuntuu siis äkkiseltään paljon monimutkaisemmalta. Tämän tekstin on tarkoitus näyttää, että tilanne on kuitenkin yksinkertaisempi kuin miltä aluksi näyttää.
25.2 Jakolasku kongruensseissa
Aloitetaan huomautuksella jakolaskusta kongruensseissa. Oletetaan, että \(p\) on alkuluku. Tutkitaan ehtoa muotoa \[ax \equiv ay \pmod{p},\] missä \(a\) on kokonaisluku, joka ei ole \(0 \pmod{p}\). Nyt siis \(ax - ay \equiv 0 \pmod{p}\), eli \[p \mid ax - ay = a(x-y).\] Koska luvun \(a\) alkutekijähajotelmassa ei ole lukua \(p\), tulee olla \(p \mid x-y\). Täten \[x \equiv y \pmod{p}.\] Voimme siis jakaa kongruenssiyhtälöstä modulo \(p\) puolittain luvun, joka ei ole nolla.
Jakolasku kongruensseissa voi tuntua hieman pelottavalta sen takia, ettei kahden kokonaisluvun jakolasku välttämättä anna kokonaislukua. Huolellisuus on toki tarpeen (koska nollalla ei edelleenkään saa jakaa ja jakolasku modulo epäalkuluvut vaatii vielä enemmän varovaisuutta), mutta silti: jakolasku kongruensseissa onnistuu.
25.3 Fermat’n pieni lause
Ensimmäinen ja yksi tärkeimmistä tuloksista, jotka esitämme, kertoo kertolaskun syklien pituuksista modulo alkuluku.
On selvää, että kertomalla lukua \(a\) itsellään päästään jossain kohtaa sykliin. On myös melko selvää, että tähän sykliin päästään \(p-1\) askeleen sisällä (koska nollasta eroavia lukuja modulo \(p\) on \(p-1\)). On kuitenkin vähemmän selvää, miksi päädymme jossakin kohtaa ykköseen, ja vielä vähemmän selvää, miksi olemme ykkösessä tasan \(p-1\) askeleen jälkeen. Esimerkiksi kuvassa 25.2 ykkösen sisältävässä syklissä on \(3\) lukua tutkittaessa moduloa \(p = 7\). Fermat’n pieni lause kertoo, ettei pituus voisi olla \(4\) tai \(5\), koska muuten \(p-1 = 6\) askeleen jälkeen ei oltaisi ykkösessä.
Todistus.
Tutkitaan kuvan 25.2 tilannetta. Oleellinen huomio on: jokaiseen lukuun tulee täsmälleen yksi nuoli. Ei siis käy niin, että jotkin luvut saisivat enemmän nuolia kuin toiset ja jotkut jäisivät ilman.
Yleisesti käy sama juttu: jos otetaan luvut \(1, 2, \ldots , p-1\) modulo \(p\), ja kerrotaan ne luvulla \(a\), niin saadaan uudestaan luvut \(1, 2, \ldots , p-1\) modulo \(p\) (mahdollisesti eri järjestyksessä kuin aiemmin), kunhan \(a\) ei ole \(0 \pmod{p}\). Tässä on vielä toisella tavalla havainnollistettu esimerkkitapaus, jossa \(a = 3\) ja \(p = 11\).
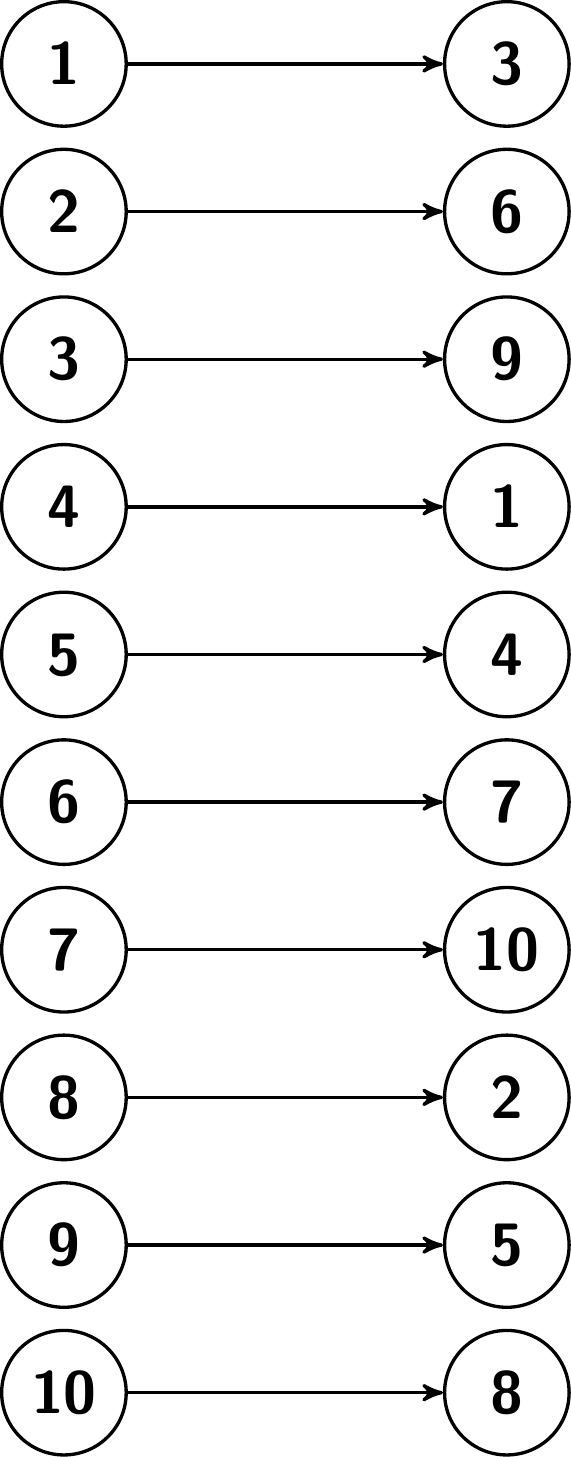
Tässä on todistus väitteelle. Todetaan ensin, että jos \(x\) ei ole \(0\) modulo \(p\), niin myöskään \(ax\) ei ole: jos kahden luvun \(a\) ja \(x\) alkutekijähajotelmassa ei ole lukua \(p\), niin myöskään niiden tulossa ei ole. Kuvan 25.3 tapauksessa tämä sanoo, ettei mikään syntyvistä oikean puolen luvuista ole \(0\).
Lisäksi mitkään kaksi syntyvistä luvuista eivät ole samoja. Jos nimittäin \(ax \equiv ay \pmod{p}\), niin jakamalla puolittain luvulla \(a\) saadaan \(x \equiv y \pmod{p}\).
Väite seuraa näistä: luvut \(a, 2a, 3a, \ldots , (p-1)a\) ovat erisuuria ja nollasta eroavia modulo \(p\), joten ne ovat \(1, 2, \ldots , p-1\) jossain järjestyksessä.
Todistetaan sitten itse Fermat’n pieni lause. Idea: Koska luvut \(a, 2a, \ldots , (p-1)a\) ovat samat kuin luvut \(1, 2, \ldots , p-1\), on näiden lukujen tulot myös samat (modulo \(p\)). Siis \[ a \cdot (2a) \cdot (3a) \cdot \ldots \cdot ((p-1)a) \equiv 1 \cdot 2 \cdot 3 \cdot \ldots \cdot (p-1) \pmod{p}. \] Vasemman puolen voi järjestellä uudestaan, jolloin saadaan yhtälö \[a^{p-1} \cdot 1 \cdot 2 \cdot 3 \cdot \ldots \cdot (p-1) \equiv 1 \cdot 2 \cdot 3 \cdot \ldots \cdot (p-1) \pmod{p}.\] Nyt jakamalla yhtälö puolittain luvulla \(1 \cdot 2 \cdot 3 \cdot \ldots \cdot (p-1)\) saadaan \[a^{p-1} \equiv 1 \pmod{p}.\]
25.4 Primitiivijuuret
Pääsemme tekstin pääaiheeseen. Johdannossa käsiteltiin sitä, kuinka yhteenlasku on yksinkertaista (kuva 25.1) ja kertolasku kaoottista (kuva 25.2). Seuraava kuva on kuitenkin selkeämpi.
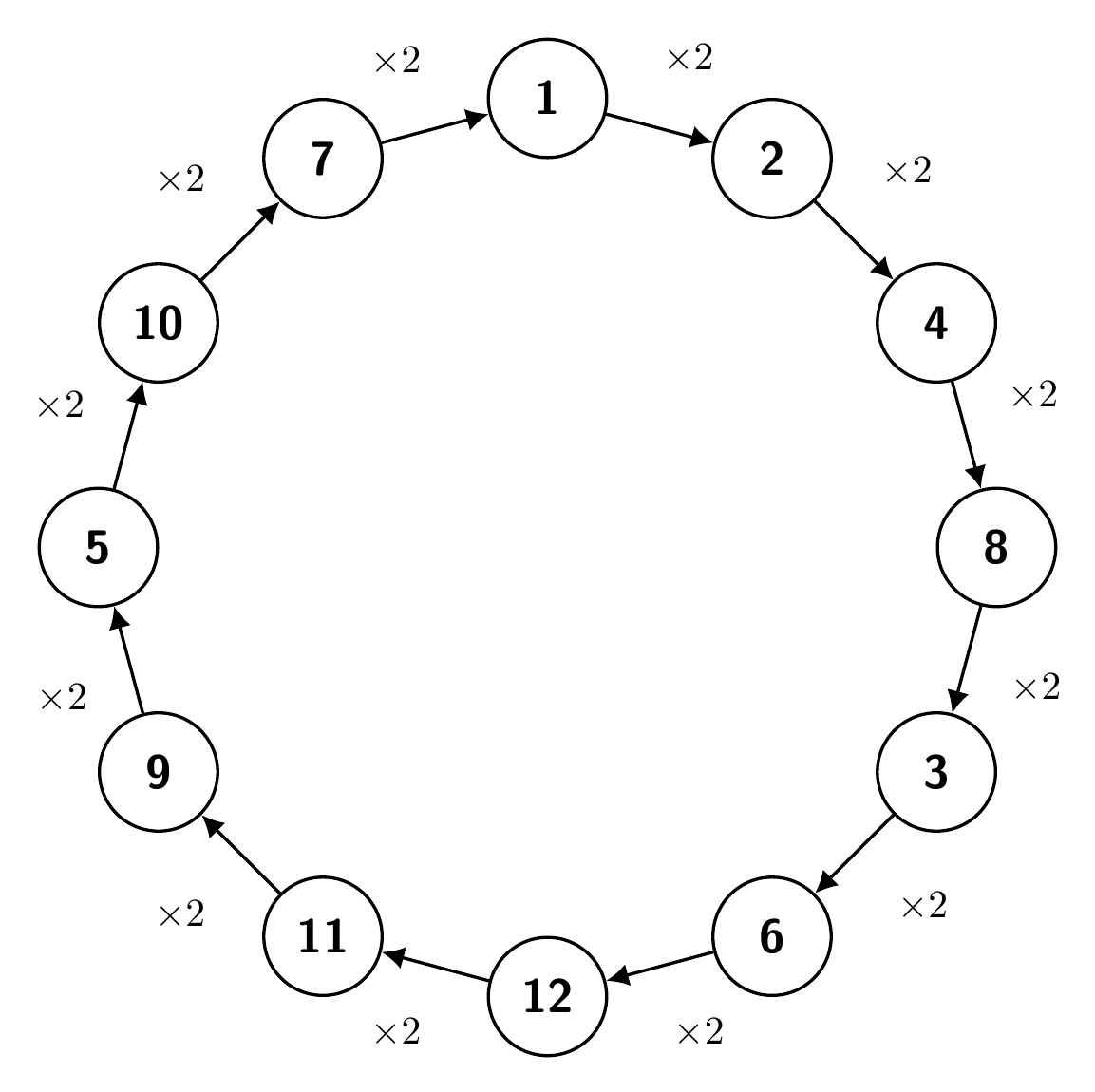
Aloittamalla luvusta \(1\) ja toistuvasti kertomalla nykyisen luvun kahdella saadaan käsiteltyä kaikki luvut modulo \(13\) (nollaa lukuun ottamatta)!
Mitä tapahtuu? Kuvassa 25.2 tutkimme samaa tilannetta, mutta saimme paljon kaoottisemman kuvan. Ongelma oli, että valitsimme väärän kertoimen: modulo \(7\) kakkonen ei toimi, mutta kolmonen toimii, sillä kolmosen potenssit modulo \(7\) antavat kaikki (nollasta eroavat) luvut.
Sattuu käymään niin, että millä tahansa alkuluvulla \(p\) on olemassa jokin luku, jolla on vastaava ominaisuus. Tällaista lukua kutsutaan primitiivijuureksi modulo \(p\). (Väitteen todistus on vaikea, minkä vuoksi se esitetään erillisessä tekstissä.)
Tämä tulos tekee kertolaskusta paljon vähemmän kaoottisen.
25.5 Esimerkkejä
Primitiivijuurien olemassaolo merkittävä tulos, joka mullistaa kongruenssien kertolaskua koskevan ajatusmaailman. Tässä on muutama esimerkki, jotka demonstroivat uutta ajattelumallia.
25.5.1 Lukuesimerkkejä
Mitä on \(8 + 7 \pmod{12}\)? Tietysti \(3 \pmod{12}\). Tämän voi havainnollistaa visuaalisesti kuvan 25.1 avulla seuraavasti: aloitetaan luvusta \(8\) ja otetaan \(7\) askelta eteenpäin. Päädymme lukuun \(3\).
Mitä on \(9 \cdot 11 \pmod{13}\)? Helppo lasku antaa vastauksen \(8 \pmod{13}\). Tämän voi havainnollistaa kuvan 25.4 avulla seuraavasti: Jos ajatellaan, että \(2\) on ringin ensimmäinen luku, \(4\) toinen, \(8\) kolmas, \(3\) neljäs ja niin edelleen, niin \(11\) on ringin seitsemäs luku. Kertolasku saadaan laskettua aloittamalla luvusta \(9\) ja ottamalla seitsemän askelta eteenpäin (missä seitsemän vastaa luvun \(11\) järjestysnumeroa ringissä). Päädymme lukuun \(8\).
Tämä voi tuntua hieman hölmöltä, koska on nopeampaa vain laskea kertolasku kuin laskea askelia jostakin kuvasta. Ajatus on kuitenkin tärkein: kertolaskun rakenne on samanlainen kuin yhteenlaskun.
25.5.2 Fermat’n pieni lause
Tutkitaan kuvan 25.1 tilannetta ja otetaan sieltä jokin luku, vaikka \(5\). Mitä saadaan, kun luku \(5\) summataan itseensä \(12\) kertaa? Tämä tietysti vastaa viittä täyttä kierrosta. Päädymme siis lukuun \(0\).
Tutkitaan kuvan 25.4 tilannetta ja otetaan sieltä jokin luku, vaikka luku \(6\). Se on ringin viides luku (kun taas ajatellaan, että \(2\) on ringin ensimmäinen luku). Mitä saadaan, kun luku \(6\) kerrotaan itsellään \(12\) kertaa? Tämä vastaa taas viittä täyttä kierrosta. Päädymme siis lukuun \(1\). Toisin sanoen \(6^{12} \equiv 1 \pmod{13}\).
Tämä on erikoistapaus Fermat’n pienestä lauseesta. Näimme osiossa 2 kovasti vaivaa lauseen todistamiseksi, mutta primitiivijuurien kautta tulkittuna väite vain sanoo, että jos kierrämme ringin ympäri jonkin määrän täysiä kierroksia, niin päädymme aloituspisteeseen.
25.5.3 Neliönjäännökset
Olemme aiemmin Diofantoksen yhtälöiden yhteydessä tehneet modulotarkasteluja ja olemme välivaiheena laskeneet, mitä arvoja \(x^2\) saa modulo \(4\). (Vastaus: \(0\) ja \(1\).) Saman kysymyksen voi kysyä muillakin moduloilla. Modulo \(13\) voidaan laskea, että \(x^2\) saa arvot \[0, 1, 3, 4, 9, 10, 12\] modulo \(13\). Näitä lukuja kutsutaan neliönjäännöksiksi modulo \(13\).1 Nollasta eroavia lukuja, jotka eivät ole neliönjäännöksiä, kutsutaan neliönepäjäännöksiksi.
1 Tarkalleen ottaen lukua \(0\) ei kutsuta neliönjäännökseksi.
Neliönjäännöksillä on paljon mielenkiintoisia ominaisuuksia. Tutkitaan tässä muutamia.
Ratkaisu: Koska \(a\) on neliö, voidaan kirjoittaa \(a \equiv x^2 \pmod{p}\). Vastaavasti voidaan kirjoittaa \(b \equiv y^2 \pmod{p}\). Nyt \((xy)^2 \equiv x^2y^2 \equiv ab \pmod{p}\).
Tämä tuntuu vaikeammalta. Tehtävä ei ratkeakaan suoraan algebrallisella manipulaatiolla kuten edellinen tehtävä.
Apuun tulee primitiivijuuri. Jos katsotaan tarkkaan, niin edellä listatut neliöt \(1, 3, 4, 9, 10\) ja \(12\) modulo \(13\) ovat täsmälleen ne luvut, jotka kuvan 25.4 ringissä esiintyvät parillisissa kohdissa \(0, 2, 4, 6, 8, 10\).
Tämä toimii yleisestikin. Jos \(g\) on primitiivijuuri modulo \(p\), niin (määritelmällisesti) luvut modulo \(p\) ovat \[g, g^2, g^3, \ldots , g^{p-1}\] jossain järjestyksessä. Näiden lukujen neliöt ovat \[g^2, g^4, g^6, \ldots , g^{2(p-1)}.\] Nämä luvut siis kiertävät kuvan 25.4 kaltaista rinkiä ympäri kahden askeleen hypyin (samaan tapaan kuin luvut \(2x, x = 0, 1, \ldots , p-1\) kiertävät kuvan 25.1 kaltaista rinkiä ympäri kahden askeleen hypyin).
Eli tehtävän väite on käytännössä sama kuin ”kahden parittoman luvun summa on parillinen”. Tämä on selvä. (Edellisen tehtävän väite puolestaan vastaa sitä, että kahden parillisen luvun summa on parillinen.)
Esitetään vielä yksi tärkeä esimerkki.
Tehtävän ratkaisemiseksi käytetään taas primitiivijuuria. Ensiksi mietitään, missä päin rinkiä luku \(-1\) on. Luku \(-1\) on sellainen, joka kerrottuna itsellään antaa luvun \(1\). Siis jos otetaan tietty määrä askelia ja päästään lukuun \(-1\), ja otetaan uudestaan sama määrä askelia, päästään lukuun \(1\). Tämä tarkoittaa, että luku \(-1\) on ringissä vastapäätä lukua \(1\). (Näin nähdään olevan kuvassa 25.4, jossa käytetään merkintää \(p-1\) merkinnän \(-1\) sijasta.) Se on siis \((p-1)/2\) askeleen päässä alusta.
Milloin on olemassa luku, jonka neliö on \(-1\)? Nähdään, että tällaisen luvun tulee olla ”kello kolmessa” tai ”kello yhdeksässä”: esimerkiksi kuvassa 25.4 luvut \(8\) ja \(5\) ovat ne, joiden neliö on \(12\).
Tässä perustelu: Jos tämä luku on \(x\) askeleen päässä aloituspisteestä, niin joko tulee olla \(2x = (p-1)/2\) tai \(2x = (p-1)/2 + (p-1)\) (jolloin \(2x\) vastaa puoltatoista kierrosta). Näistä yhtälöistä saadaan ratkaistua, että \(x = (p-1)/4\) tai \(x = 3(p-1)/4\) (eli \(x\) on joko kello kolmessa tai kello yhdeksässä). Nämä luvun \(x\) arvot ovat kokonaislukuja täsmälleen silloin, kun \(p \equiv 1 \pmod{4}\).
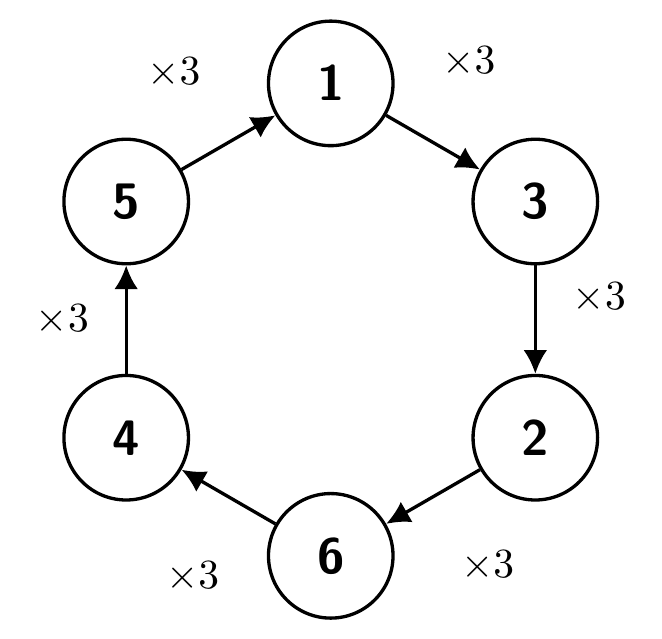
Huomataankin, että esimerkiksi kuvan 25.5 tilanteessa yksikään luku ei ole kello kolmessa tai kello yhdeksässä. Tämä johtuu siitä, että puolikkaan kierroksen pituus \((p-1)/2\) on pariton, eli siitä että \(p \equiv 3 \pmod{4}\).
25.6 Tehtäviä
Tehtävä 1.
- Etsi kullekin alkuluvuista \(2, 3, 5, 7, 11, 13\) ja \(17\) vähintään yksi primitiivijuuri.
- Etsi näitä alkulukuja vastaavat neliönjäännökset.
Tehtävä 2. Etsi kaikki primitiivijuuret modulo \(13\). Miten ne asettuvat kuvaan 25.4?
Tehtävä 3. Olkoon \(p\) alkuluku. Oletetaan, että \(a\) on neliönjäännös modulo \(p\) ja \(b\) on neliönepäjäännös. Osoita, että \(ab\) on neliönepäjäännös modulo \(p\).
Tehtävä 4. Olkoon \(p\) alkuluku. Tutkitaan lukuja \(x^2 \pmod{p}\), missä \(x\) käy läpi luvut \(1, 2, 3, \ldots , p-1\). Osoita, että tällä tavalla saatavia erisuuria lukuja on tasan \((p-1)/2\) kappaletta.
Tehtävä 5. Olkoon \(p\) alkuluku. Tutkitaan lukuja \(x^3 \pmod{p}\), missä \(x\) käy läpi luvut \(1, 2, 3, \ldots , p-1\). Osoita, että
- jos \(p \equiv 2 \pmod{3}\), niin tällä tavalla saatavia erisuuria lukuja on tasan \(p-1\) kappaletta
- jos \(p \equiv 1 \pmod{3}\), niin tällä tavalla saatavia erisuuria lukuja on tasan \((p-1)/3\) kappaletta.
Tehtävä 6. Luvun \(a\) aste modulo \(p\) on pienin positiivinen kokonaisluku \(n\), jolla \(a^n \equiv 1 \pmod{p}\). Esimerkiksi luvun \(2\) aste modulo \(7\) on kolme, koska \(2^1\) ja \(2^2\) eivät ole \(1 \pmod{7}\), mutta \(2^3\) on. Laske lukujen \(1, 2, 3, \ldots , 12\) asteet modulo \(13\).
Tehtävä 7. Olkoon \(p\) alkuluku ja \(x\) luku, joka ei ole \(0 \pmod{p}\).
- Olkoon \(m\) luvun \(x\) aste modulo \(p\). Osoita, että jos \(a\) on positiivinen kokonaisluku, niin \(x^a \equiv 1 \pmod{p}\) pätee täsmälleen silloin, kun \(a\) on jaollinen luvulla \(m\).
- Oletetaan, että \(a\) ja \(b\) ovat positiivisia kokonaislukuja, joilla \(x^a \equiv 1 \pmod{p}\) ja \(x^b \equiv 1 \pmod{p}\). Olkoon \(d\) lukujen \(a\) ja \(b\) suurin yhteinen tekijä. Osoita, että \(x^d \equiv 1 \pmod{p}\).
- Todista, että minkä tahansa luvun aste modulo \(p\) jakaa luvun \(p-1\).