2 Kehäkulmalause

Tekijä

Olli Järviniemi

2.1 Johdanto

Tärkeimpiä asioita geometriassa on kulmien suuruudet ja niiden laskeminen. Perustyökaluja ovat jo peruskoulusta tutut faktat ”kolmion kulmien summa on \(180\) astetta”, ”ristikulmat ovat yhtä suuret”, ”tasakylkisen kolmion kantakulmat ovat yhtä suuret” ja niin edelleen. Tässä tekstissä esitellään kehäkulmalause, joka on vahva työkalu kulmien laskemiseen.

2.2 Kehäkulmalause

Tutkitaan seuraavaa kuvaa.

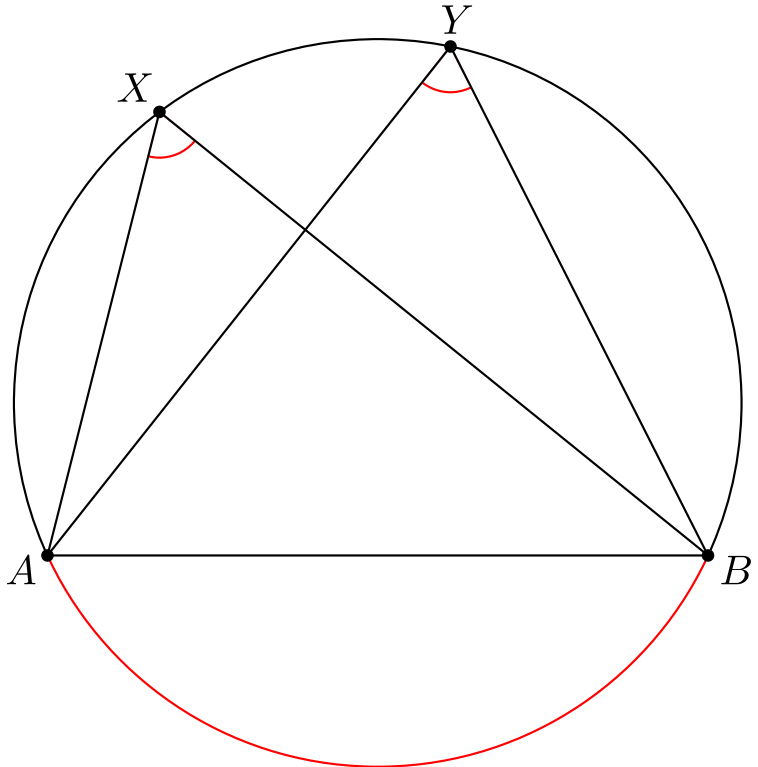
Pisteet \(A, B, X\) ja \(Y\) ovat siis mielivaltaisia pisteitä ympyrän kehällä. Kehäkulmalause sanoo, että punaisella merkityt kulmat ovat yhtä suuret.

Lause 2.1 (Kehäkulmalause) Olkoot \(A, B, X\) ja \(Y\) (eri) pisteitä ympyrän kehällä. Oletetaan, että \(X\) ja \(Y\) ovat samalla puolella janaa \(AB\). Tällöin \(\angle AXB = \angle AYB\).

Toisin sanoen samaa kaarta (kuvassa punaisella) vastaavat kehäkulmat ovat yhtä suuria.

Huomaa lauseen oletus pisteiden \(X\) ja \(Y\) sijainnista. Tämä oletus on välttämätön, kuten seuraavasta kuvasta nähdään: toinen kulmista näyttää olevan tylppä ja toinen terävä.

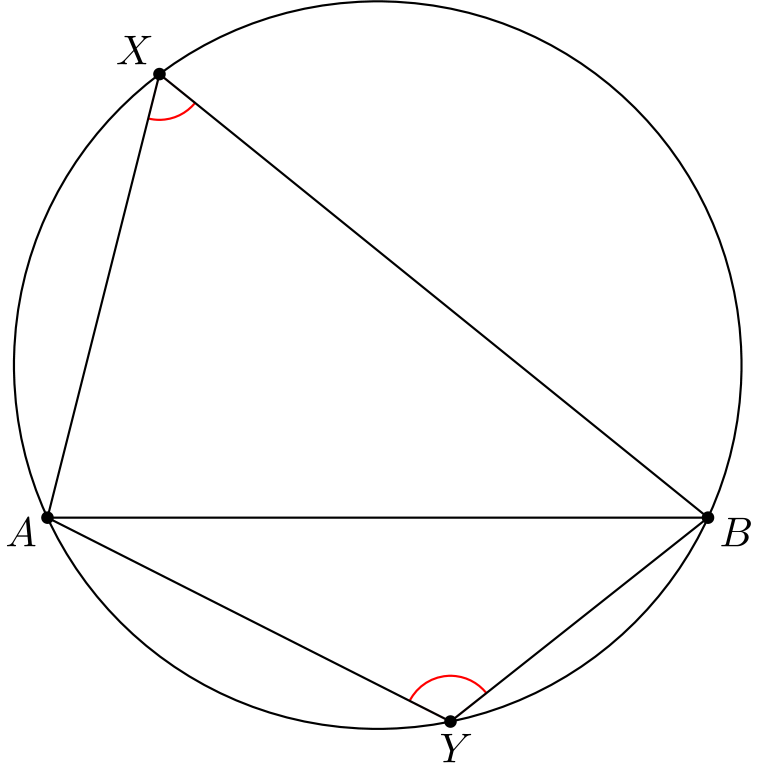
Tilanne muuttuu, jos \(X\) ja \(Y\) ovat eri puolilla janaa \(AB\).

Tähän tilanteeseen palataan alempana.

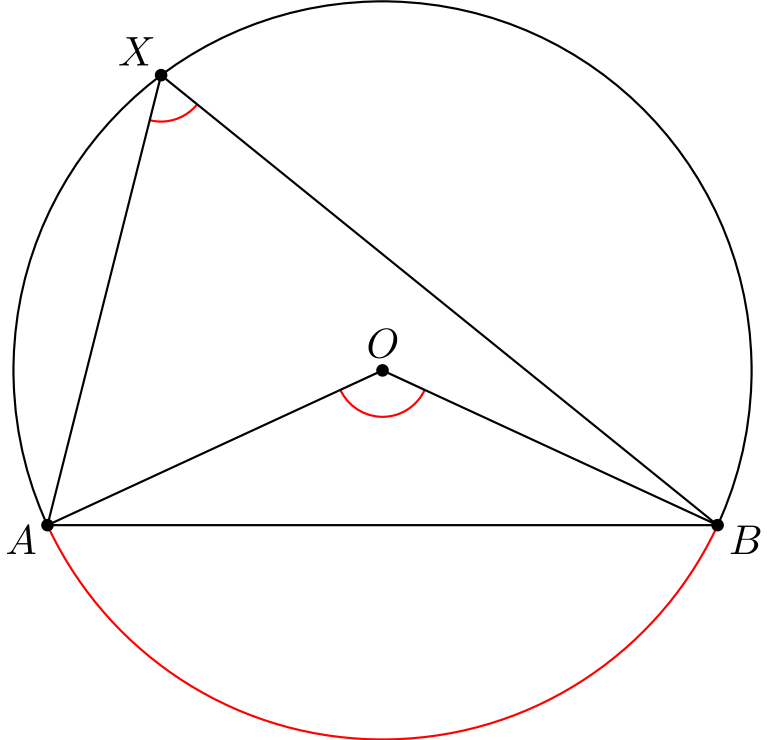
Kehäkulmalauseesta on toinen versio, joka yhdistää kehäkulman ja ns. keskuskulman suuruudet toisiinsa: keskuskulma on kaksinkertainen kehäkulmaan verrattuna.

Lause 2.2 (Kehäkulmalauseen keskuskulmaversio) Olkoot \(A, B\) ja \(X\) (eri) pisteitä ympyrän kehällä, ja olkoon \(O\) ympyrän keskipiste. Tällöin pätee \(\angle AOB = 2 \angle AXB\).

2.3 Kehäkulmalauseen todistus

Todistamme kehäkulmalauseen keskuskulmaversion. Tästä seuraa, että kaikki samaa kaarta vastaavat kehäkulmat ovat yhtä suuria, koska jokainen niistä on puolet kaarta vastaavasta keskuskulmasta.

Tutkitaan siis seuraavaa kuvaa. Kuvaan on merkitty avuksi suoran \(XO\) leikkauspiste janan \(AB\) kanssa.¹

¹ Todistuksessa pitäisi oikeasti olla tarkempi tapauksien kanssa (entä jos leikkauspiste ei olisikaan \(A\):n ja \(B\):n välissä?), mutta muut tapaukset saa käsiteltyä samaan tapaan, joten ei juututa tähän.

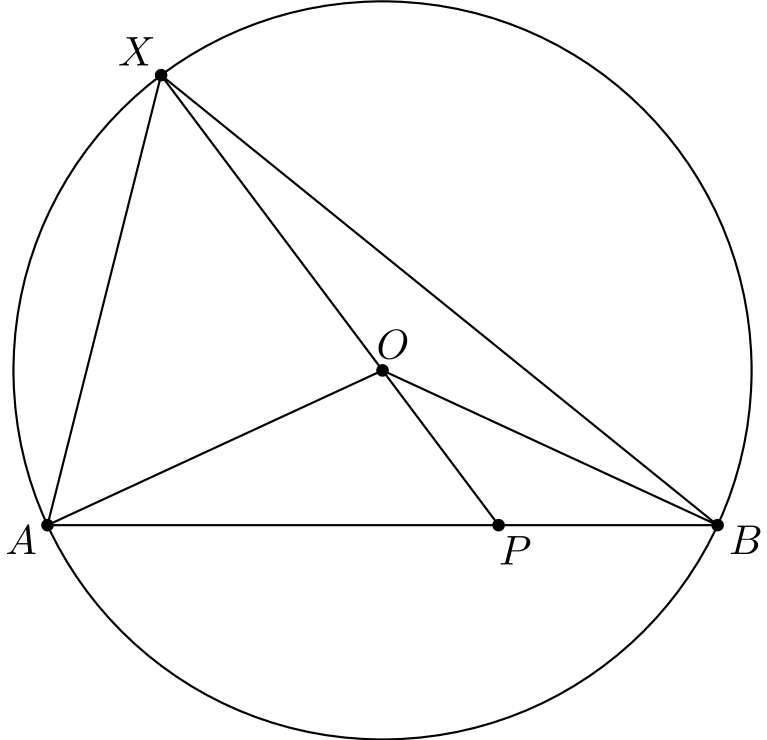
Suora \(XO\) leikkaa janan \(AB\) pisteessä \(P\).

Merkitään kulmaa \(\angle AXO\) kirjaimella \(\alpha\). Koska ympyrän säteet \(OA\) ja \(OX\) ovat yhtä pitkät, kolmio \(AOX\) on tasakylkinen ja siten myös toinen kantakulma \(\angle OAX\) on suuruudeltaan \(\alpha\). Koska kolmion kulmien summa on \(180\) astetta, saadaan laskettua kolmion huippukulma: \[\angle XOA = 180^{\circ} - \alpha - \alpha = 180^{\circ} - 2\alpha.\] Oikokulma on \(180^{\circ}\), joten \[\angle AOP = 180^{\circ} - \angle XOA = 180^{\circ} - (180^{\circ} - 2\alpha) = 2\alpha.\]

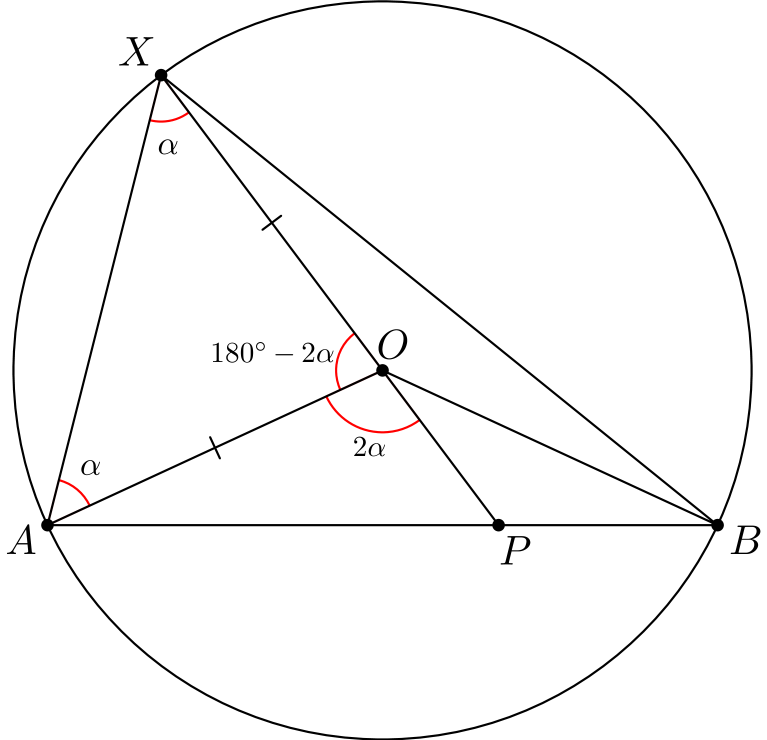
Olemme siis todistaneet, että \(\angle AOP\) on kaksinkertainen kulmaan \(\angle AXP\) verrattuna. Vastaavilla laskuilla saadaan todistettua, että \(\angle POB\) on kaksinkertainen kulmaan \(\angle PXB\) verrattuna. Täten koko keskuskulma \(\angle AOB\) on kaksinkertainen kulmaan \(\angle AXB\) verrattuna, mikä oli todistettavana.

2.4 Kehäkulmalause vastakkaisille kulmille

Tutkitaan vielä tapausta, jossa kehäkulmat ovat eri puolilla vastaavaa janaa.

Kuten aiemmin todettiin, kehäkulmat eivät tässä tapauksessa ole samat. Niillä on kuitenkin vahva yhteys: niiden summa on \(180\) astetta.

Lause 2.3 (Kehäkulmalause vastakkaisille kulmille) Olkoot \(A, B, X\) ja \(Y\) mielivaltaiset (eri) pisteet ympyrän kehällä. Oletetaan, että \(X\) ja \(Y\) ovat eri puolilla janaa \(AB\). Tällöin \(\angle AXB + \angle BYA = 180^{\circ}\).

Ajatuksena on, että \(\angle AXB\) ja \(\angle BYA\) ovat kaksi kehäkulmaa, jotka yhdessä vastaavat koko ympyrän kehää.

Todistus perustuu kehäkulmalauseen keskuskulmaversioon. Tutkitaan seuraavaa kuvaa.

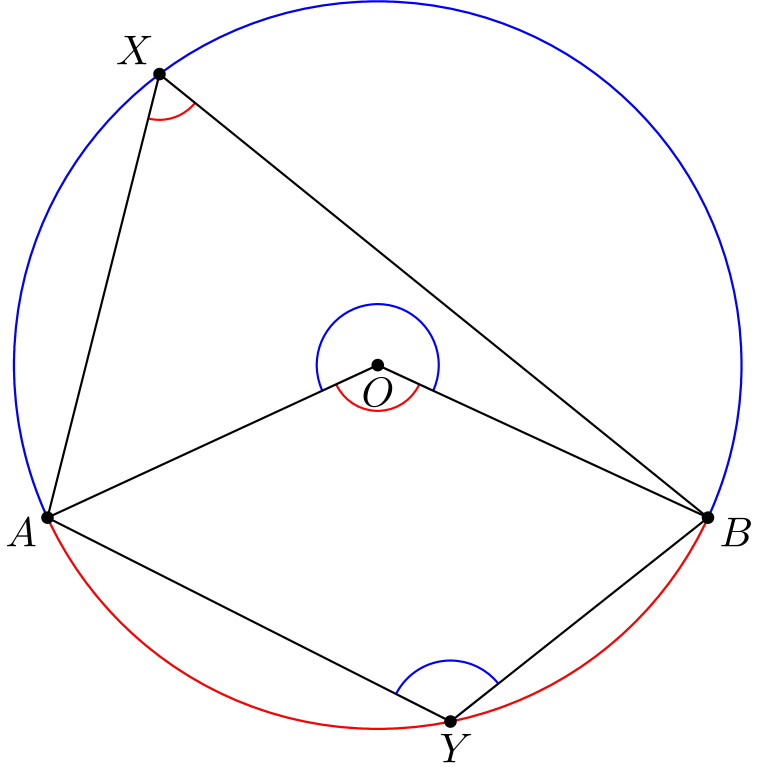
Olemme yllä todistaneet, että kehäkulma on puolet keskuskulmasta, eli \[\angle AXB = \frac{1}{2}\angle AOB\] (kuvan punaiset kulmat). Tämä toimii myös, vaikka keskuskulma olisi yli \(180\) astetta, kuten kuvan sininen keskuskulma \(\angle BOA\). Siis sininen kehäkulma on puolet sinisestä keskuskulmasta: \[\angle BYA = \frac{1}{2}\angle BOA\] Keskuskulmien summan suuruus on täysi kulma eli \(360\) astetta, joten kehäkulmien summa on puolet tästä, \(180\) astetta.

2.5 Tehtäviä

Tässä on kulmien laskemista käsitteleviä tehtäviä. Pidä erityisesti kehäkulmalauseen eri versiot mielessä, mutta älä unohda myöskään muita perustyökaluja. Tehtävät vaikeutuvat loppua kohti. (Vaikeimpiin tehtäviin voi myös palata myöhemmin.)

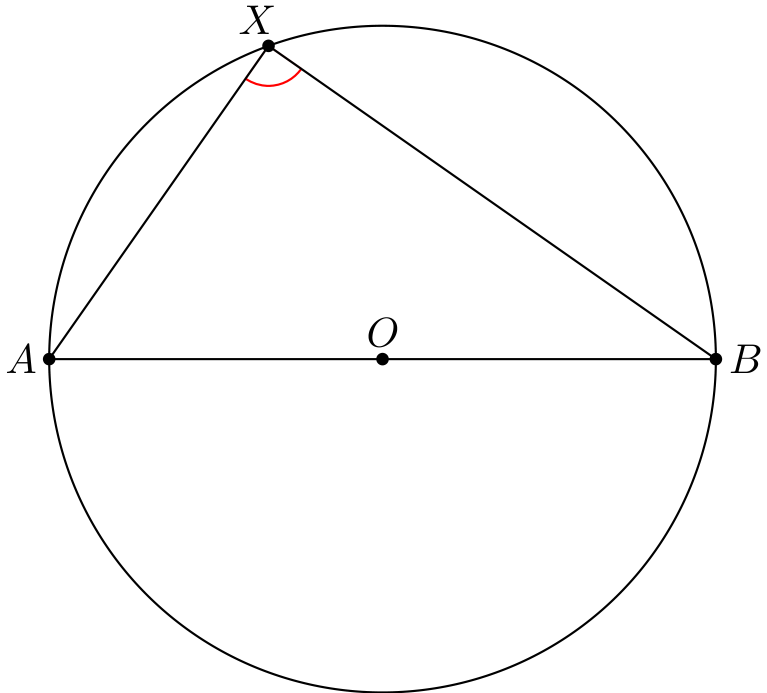
Tehtävä 1 \(AB\) on ympyrän halkaisija, ja \(X\) on piste ympyrän kehällä. Kuinka suuri on kulma \(\angle AXB\) (kuvassa punaisella)?

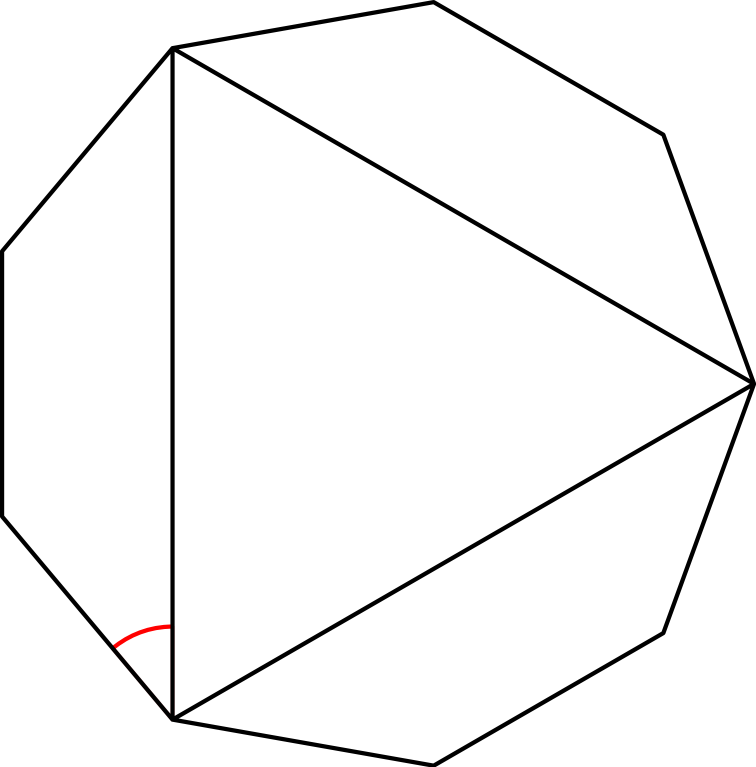
Tehtävä 2. Alla olevassa kuvassa on tasasivuinen kolmio ja säännöllinen yhdeksänkulmio. Laske punaisella merkitty kulma.

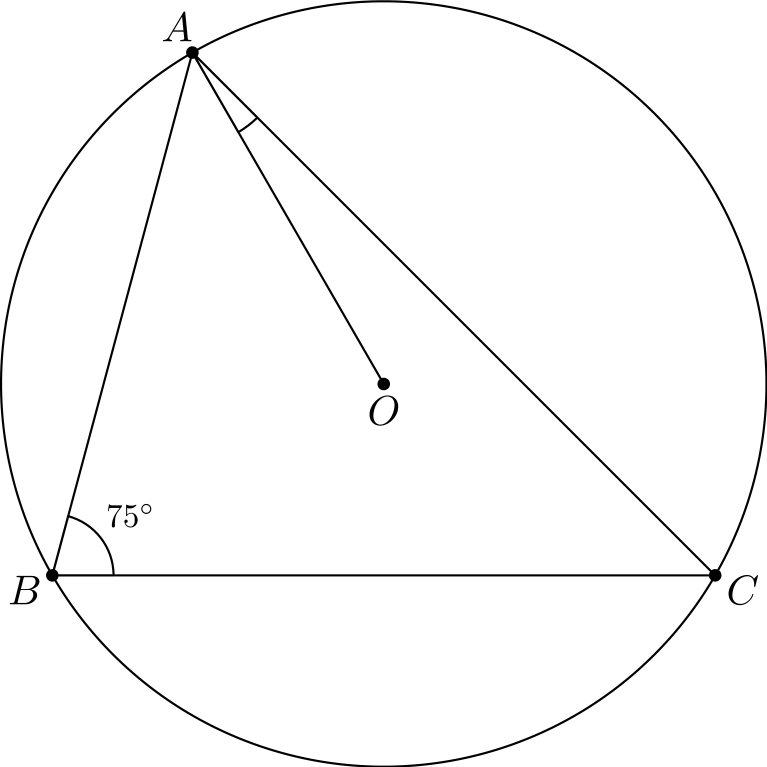
Tehtävä 3. Pisteet \(A, B\) ja \(C\) ovat ympyrän kehällä. Ympyrän keskipiste on \(O\). Tiedetään, että \(\angle CBA = 75^{\circ}\). Kuinka suuri on kulma \(\angle OAC\)?

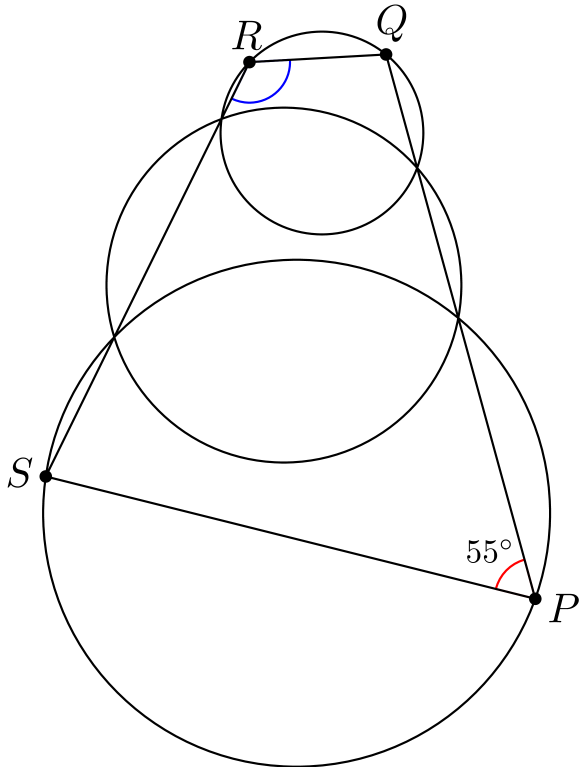
Tehtävä 4. Kuvassa on kolme ympyrää ja nelikulmio \(PQRS\). Janat \(PQ\) ja \(RS\) kulkevat ympyröiden leikkauspisteiden kautta. Tiedetään, että \(\angle QPS = 55^{\circ}\). Laske kulma \(\angle SRQ\).

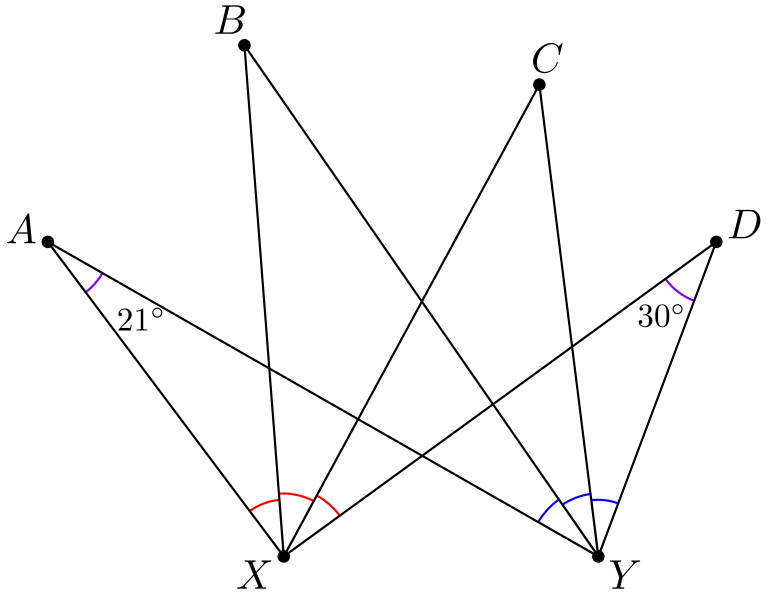
Tehtävä 5. Kuvassa on kuusi pistettä \(A, B, C, D, X\) ja \(Y\). Tiedetään, että \(\angle BXA = \angle CXB = \angle DXC\) (kuvassa punaisella) ja \(\angle BYA = \angle CYB = \angle DYC\) (kuvassa sinisellä). Lisäksi tiedetään, että \(\angle XAY = 21^{\circ}\) ja \(\angle XDY = 30^{\circ}\) (kuvassa violetilla). Kuinka suuria ovat kulmat \(\angle XBY\) ja \(\angle XCY\)?

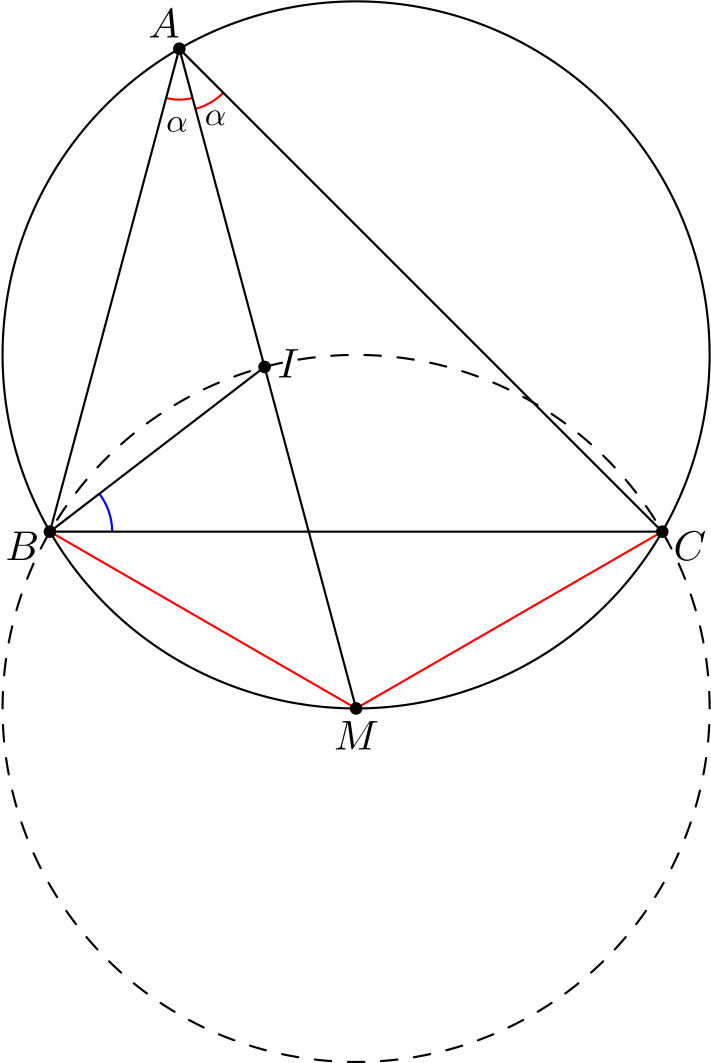
Tehtävä 6. Kuvassa pisteet \(A, B\) ja \(C\) ovat samalla ympyrällä. Ympyrällä on piste \(M\) niin, että \(AM\) puolittaa kulman \(\angle BAC\), eli \(\angle BAM = \alpha\) ja \(\angle MAC = \alpha\) (kuvassa sinisellä).

Osoita, että janat \(MB\) ja \(MC\) ovat yhtä pitkät.
Piirretään ympyrä, jonka keskipiste on \(M\) ja joka kulkee pisteen \(B\) kautta. Tämä ympyrä leikkaa janan \(AM\) pisteessä \(I\). Osoita, että \(\angle CBI\) on puolet kulmasta \(\angle CBA\).

Huomautus:

Piste \(I\) on siis kolmion \(ABC\) kulmien \(\angle BAC\) ja \(\angle CBA\) puolittajien leikkauspiste. b-kohdan todistus toimii symmetrisesti myös sen osoittamiseen, että \(CI\) puolittaa kulman \(\angle ACB\). Tehtävästä 6 saadaan siis, että kolmion \(ABC\) kolme kulmanpuolittajaa leikkaavat samassa pisteessä (joka on tehtävän piste \(I\)). Tämä ei ole itsestäänselvyys: kolmella suoralla ei tietenkään aina ole yhteistä leikkauspistettä. Tämä tulos on tärkeä, ja siihen tullaan palaamaan myöhemmin useaan kertaan.

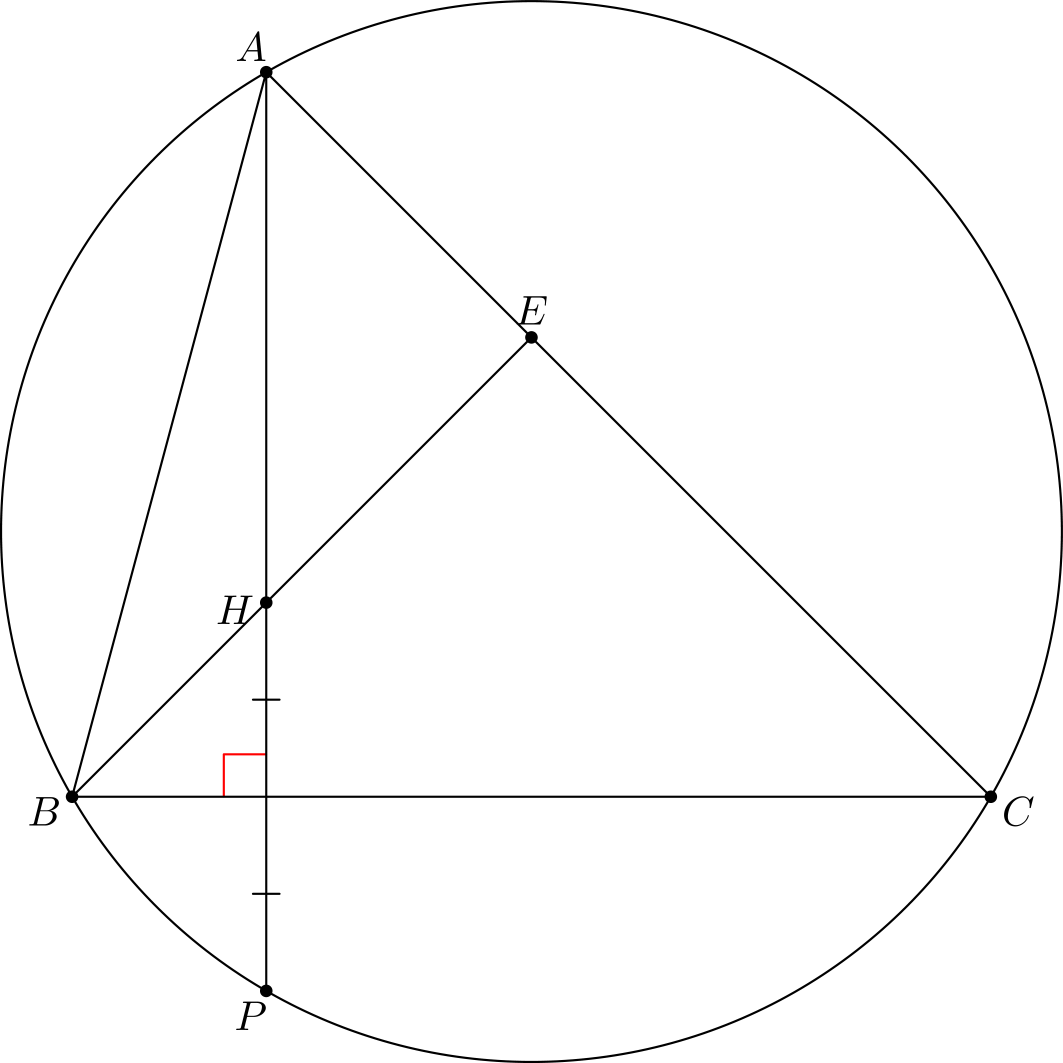
Tehtävä 7. Kuvassa pisteet \(A, B\) ja \(C\) ovat samalla ympyrällä. Ympyrällä on piste \(P\) niin, että \(AP\) ja \(BC\) ovat kohtisuorassa toisiinsa nähden. Piste \(H\) on pisteen \(P\) peilaus janan \(BC\) yli. Janan \(BH\) jatke leikkaa janan \(AC\) pisteessä \(E\). Osoita, että kulma \(\angle BEC\) on \(90^{\circ}\).

Huomautus:

Piste \(H\) on siis kolmion \(ABC\) kärjistä \(A\) ja \(B\) piirrettyjen korkeusjanojen leikkauspiste. Tehtävän todistus toimii symmetrisesti myös sen osoittamiseen, että jos \(F\) on janan \(CH\) jatkeen leikkauspiste janan \(AB\) kanssa, niin \(\angle BFC\) on \(90^{\circ}\). Saadaan siis, että kolmion \(ABC\) korkeusjanat leikkaavat samassa pisteessä, joka on tehtävän piste \(H\). Kuten tehtävän 6 tulos, myös tämä on tärkeä juttu, johon tullaan palaamaan myöhemmin useaan kertaan.