18 Aritmetiikan peruslauseen todistus

Tekijä

Olli Järviniemi

18.1 Johdanto

Tässä tekstissä esitetään aritmetiikan peruslauseen todistus. Todistus tulee käyttämään niin kutsuttua Bezout’n lemmaa, joten aloitamme tekstin siitä.

18.2 Eräs Diofantoksen yhtälö

Diofantoksen yhtälöitä on käsitelty jo omassa tekstissään. Tässä käsitellään tietyntyyppisiä Diofantoksen yhtälöitä, joista alla oleva tehtävä on yksi esimerkki.

Tehtävä 18.1 Etsi kaikki kokonaisluvut \(x\) ja \(y\), joilla \[7x - 5y = 2.\]

Huomataan pieni ratkaisu \(x = 1\), \(y = 1\), mutta muita pieniä ratkaisuja ei heti näy.

Yhtälöstä voi ratkaista luvun \(y\) luvun \(x\) avulla: \[y = \frac{7x - 2}{5}.\] Tästä saatava \(y\) on kokonaisluku täsmälleen silloin, kun \(7x - 2\) on jaollinen viidellä, eli kun \[7x \equiv 2 \pmod{5}.\] Käymällä läpi viisi vaihtoehtoa luvun \(x\) arvoille modulo \(5\) huomataan, että tämä yhtälö pätee täsmälleen silloin, kun \(x \equiv 1 \pmod{5}\).

Eli kaikki ratkaisut saadaan valitsemalla jokin kokonaisluku \(x\), joka on \(1 \pmod{5}\), ja sitten valitsemalla \(y = (7x - 2)/5\).

Tästä on ehkä hieman vaikea hahmottaa, miltä ratkaisut oikeasti näyttävät. Ratkaisujoukkoa voi ajatella näin: Alussa huomasimme yhden ratkaisun \(x = 1, y = 1\). Muut kelpaavat \(x\):n arvot saadaan kasvattamalla tai pienentämällä \(x\):ää viidellä jonkin määrän kertoja. Tutkimalla yhtälöä \[7x - 5y = 2\] huomataan, että jos \(x\):ää kasvatetaan viidellä, niin \(y\):tä tulee kasvattaa seitsemällä, jotta vasemman puolen arvo ei muutu. Vastaavasti jos \(x\) pienenee viidellä, niin \(y\):n tulee pienentyä seitsemällä.

Tässä on taulukko ratkaisuista. Vasemmalla on kelpaavia \(x\):n arvoja ja oikealla näitä \(x\):n arvoja vastaavat \(y\):n arvot.

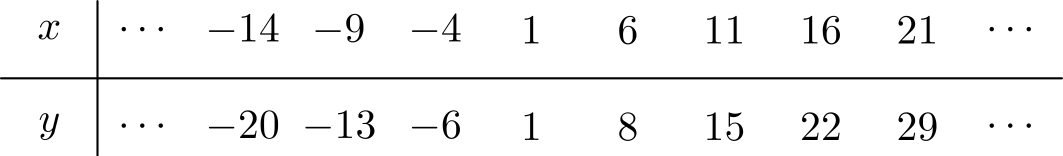
Tässä on vielä yksi tapa sanoa, mitkä luvut kelpaavat: ratkaisut saadaan valitsemalla jokin kokonaisluku \(k\) ja asettamalla \(x = 5k + 1\) ja \(y = 7k + 1\). Taulukko vastaa tapauksia, joissa \(k = -3, -2, -1, \ldots , 4\).

18.3 Bezout’n lemma

Bezout’n lemma kertoo yleisesti, että yhtälöillä muotoa \(ax + by = c\) on ratkaisu, jos \(a\) ja \(b\) ovat yhteistekijättömiä.

Lause 18.1 (Bezout’n lemma) Olkoot \(a, b\) ja \(c\) kokonaislukuja. Oletetaan, että lukujen \(a\) ja \(b\) suurin yhteinen tekijä on \(1\). Tällöin yhtälöllä \[ax + by = c\] on äärettömän monta kokonaislukuratkaisua.

(Väite ei päde, jos oletusta suurimmasta yhteisestä tekijästä ei tehdä: tietystikään esimerkiksi yhtälöllä \(3x + 6y = 2\) ei ole ratkaisua, koska vasen puoli on aina jaollinen kolmella, kun taas oikea puoli ei ole.)

Lauseen todistus on melko vaikea, mutta lauseen tärkeydestä johtuen todistus on paikallaan.

Todistus. Tutkitaan yksinkertaisuuden vuoksi tapausta, jossa \(a\) ja \(b\) ovat positiivisia. Muut tapaukset käsitellään samalla tavalla.¹ Todistus perustuu induktiiviseen päättelyyn.

¹ Muut tapaukset seuraavat tästä oikeastaan suoraan. Kuvitellaan nimittäin, että olemme todistaneet, että vaikkapa yhtälöllä \(7x + 5y = 2\) on äärettömän monta ratkaisua. Nyt jos \(x = n, y = m\) on yksi ratkaisu tälle yhtälölle, niin \(x = n, y = -m\) on ratkaisu yhtälölle \(7x - 5y = 2\). Täten myös yhtälöllä \(7x - 5y = 2\) on äärettömän monta ratkaisua. Vastaavilla merkin vaihtamisilla huomataan, että myös yhtälöillä \(-7x + 5y = 2\) ja \(-7x - 5y = 2\) on äärettömän monta ratkaisua.

Tutkitaan ensin pieniä tapauksia:

\(a = b = 1\): Yhtälöllä \(x + y = c\) on äärettömän monta kokonaislukuratkaisua. Voidaan nimittäin valita \(x\) olemaan mikä tahansa kokonaisluku ja sitten valita \(y = c - x\).
\(a = 2, b = 1\): Yhtälöllä \(2x + y = c\) on äärettömän monta kokonaislukuratkaisua. Voidaan nimittäin taas valita \(x\) miten tahansa ja sitten valita \(y = c - 2x\).
\(a = 1, b = 2\): Yhtälöllä \(x + 2y = c\) on äärettömän monta kokonaislukuratkaisua. Tällä kertaa valitaan \(y\) miten tahansa ja sitten \(x = c - 2y\).

Ainakin pienillä tapauksilla väite pätee. Todistetaan sitten, että väite pätee myös suuremmilla tapauksilla. Ideana on redusoida isommat tapaukset pienempiin tapauksiin.

Valitaan jotkin positiiviset kokonaisluvut \(a\) ja \(b\). Todistetaan, että yhtälöllä \(ax + by = c\) on äärettömän monta kokonaislukuratkaisua. Riittää tutkia tapausta \(a \ge b\), koska tapaus \(a \le b\) on samanlainen. Tapaus \(a = b\) on kielletty, jos \(a > 1\), koska oletimme, että luvuilla \(a\) ja \(b\) ei ole yhteisiä tekijöitä.

Tutkitaan siis tapausta, jossa \(a > b\). Kirjoitetaan yhtälö muotoon \((a - b)x + b(x+y) = c\). Kuvitellaan hetkeksi, että olemme todistaneet, että yhtälöllä \((a-b)X + bY = c\) on äärettömän monta kokonaislukuratkaisua \((X, Y)\). Tämän yhtälön ratkaisusta saadaan yhtälölle \((a-b)x + b(x+y) = c\) ratkaisu: valitaan \(x = X\) ja \(y = Y - X\). Täten tässä tapauksessa myös yhtälöllä \((a-b)x + b(x+y) = c\) eli \(ax + by = c\) on äärettömän monta ratkaisua.

Eli enää riittää todistaa, että yhtälöllä \((a-b)X + bY = c\) todella on äärettömän moonta kokonaislukuratkaisua. Mutta tämä on pienempi tapaus kuin yhtälö \(ax + by = c\), josta lähdimme liikkeelle! Toistamalla tätä prosessia pääsemme yhä pienempiin ja pienempiin yhtälöihin. Pienten tapausten toimivuus tarkistettiin yllä, eli tämä on kunnossa.

Vielä yksi juttu: Todistuksessa tulee ottaa huomioon se, että lukujen \(a\) ja \(b\) suurin yhteinen tekijä on \(1\). Erityisesti pitää tarkistaa se, että yllä tutkittavassa pienemmässä yhtälössä \((a-b)X + bY = c\) sama ehto pätee. Toisin sanoen pitää todistaa seuraava väite: jos luvuilla \(a\) ja \(b\) ei ole yhteisiä tekijöitä (paitsi \(1\)), niin myöskään luvuilla \(a-b\) ja \(b\) ei ole. Mutta tämä on helppoa: jos olisi jokin luku \(d > 1\), joka jakaa molemmat luvuista \(a-b\) ja \(b\), niin se jakaisi myös luvun \((a-b) + b = a\), eli se jakaisi molemmat luvuista \(a\) ja \(b\). Tämä ei käy, joten \(a-b\) ja \(b\) ovat yhteistekijättömiä.

Bezout’n lemma on näin ollen todistettu.

Huomautus. Samaan tapaan voidaan selvittää yhtälön ratkaisut. Idea on sama kuin esimerkkitapauksessa \(7x - 5y = 2\): Valitaan yksi ratkaisu \((x, y)\). Muut ratkaisut saadaan lisäämällä tai vähentämällä lukuun \(x\) luvun \(b\) jonkin määrän kertoja ja vähentämällä tai lisäämällä lukuun \(y\) luvun \(a\) saman määrän kertoja.

18.4 Aritmetiikan peruslauseen todistus

Pääsemme sitten itse asiaan eli aritmetiikan peruslauseen todistukseen.

Kerrataan vielä lauseen tarkka muotoilu.

Lause 18.2 (Aritmetiikan peruslause) Jokainen positiivinen kokonaisluku voidaan esittää täsmälleen yhdellä tavalla alkulukujen tulona, kun tulon tekijöiden järjestystä ei huomioida.

(Ykkösen alkutekijähajotelman ajatellaan olevan tyhjä, eli siinä on nolla alkulukua.)

Osoitetaan ensin, että tapoja on vähintään yksi. Tämä on helpompi osuus todistuksesta. Todistus perustuu induktiiviseen päättelyyn.

Valitaan jokin positiivinen kokonaisluku \(n\). Jos \(n\) on jaollinen jollakin luvulla \(k\), joka on suurempi kuin \(1\) ja pienempi kuin \(n\), niin voidaan kirjoittaa \(n = mk\), missä \(m\) on positiivinen kokonaisluku. Jos luvut \(m\) ja \(k\) voidaan esittää jollakin tavalla alkulukujen tulona, voidaan myös \(n\) esittää. Voimme täten induktiivisesti redusoida ongelman pienempään tapaukseen.

Jos taas \(n\) ei ole jaollinen millään tällaisella luvulla \(k\), niin \(n\) on alkuluku. Tässä tapauksessa väite on selvä: \(n\):n alkutekijähajotelma koostuu vain alkuluvusta \(n\).

Todistetaan sitten, että tapoja ei ole enempää kuin yhtä. Tätä varten tarvitsemme Eukleideen lemmana tunnetun tuloksen.

Apulause 18.1 Oletetaan, että alkuluku \(p\) jakaa kahden kokonaisluvun \(a\) ja \(b\) tulon \(ab\). Tällöin \(p\) jakaa vähintään yhden luvuista \(a\) ja \(b\).

(Väite selvästi pätee jos oletetaan, että aritmetiikan peruslause pätee. Käytämme kuitenkin tätä tulosta lauseen todistamiseen, joten lemman todistus pitää saada muuta kautta. Todistus on tämän vuoksi hieman erikoinen.)

Lemman todistus. Jos \(p\) jakaa luvun \(a\), olemme valmiit. Tutkitaan tapausta, jossa \(p\) ei jaa lukua \(a\). Tällöin \(\text{syt}(a, p) = 1\), koska alkuluvun määritelmän nojalla luvun \(p\) tekijöitä ovat vain \(1\) ja \(p\). Täten Bezout’n lemman nojalla on olemassa kokonaisluvut \(x\) ja \(y\), joilla \[ax + py = 1.\] Kerrotaan yhtälö puolittain luvulla \(b\): \[abx + bpy = b.\] Oletuksen nojalla luku \(p\) jakaa tulon \(ab\). Tietysti \(p\) jakaa myös luvun \(bpy\). Täten \(p\) jakaa yhtälön vasemman puolen ja siten oikean puolen luvun \(b\). Tämä todistaa väitteen.

Aritmetiikan peruslauseen yksikäsitteisyysosan todistus.

Kuvitellaan, että väite ei päde. Valitaan pienin positiivinen kokonaisluku \(n\), joka voidaan esittää vähintään kahdella eri tavalla alkulukujen tulona. Kirjoitetaan siis \[n = p_1p_2 \cdots p_m = q_1q_2 \cdots q_k,\] missä \(p_1, p_2, \ldots , p_m, q_1, \ldots , q_k\) ovat alkulukuja. Tutkitaan yhtälöä \[p_1p_2 \cdots p_m = q_1q_2 \cdots q_k.\]

Yhtälön vasen puoli on jaollinen luvulla \(p_1\), joten myös oikea puoli on. Siis \(p_1\) jakaa tulon \(q_1 \cdots q_k\). Käyttämällä Eukleideen lemmaa monta kertaa saadaan, että \(p_1\) jakaa vähintään yhden tämän tulon luvuista, vaikkapa luvun \(q_i\).

Koska \(q_i\) on alkuluku, tarkoittaa tämä, että \(p_1 = q_i\). Tästä seuraa, että \[n/p_1 = p_2p_3 \cdots p_m = q_1q_2 \cdots q_{i-1}q_{i+1} \cdots q_k.\] Täten luku \(n/p_1\) voidaan esittää (vähintään) kahdella eri tavalla alkulukujen tulona. Mutta oletimme, että \(n\) on pienin luku, jolla on tämä ominaisuus. Ristiriita!

Eli kuvitteellinen tilanne, jossa jotkin luvut voidaan esittää useammalla tavalla alkulukujen tulona, ei toimi. Aritmetiikan peruslause siis pätee.

18.5 Lineaariset yhtälöt kongruensseissa

Päätetään teksti kommenttiin lineaarisista yhtälöistä kongruensseissa.

Bezout’n lemman yhtälöt muotoa \(ax + by = c\) liittyvät vahvasti lineaarisiin yhtälöihin kongruensseissa. Esimerkiksi alun esimerkin yhtälön \(7x - 5y = 2\) ratkaiseminen perustui kongruenssiyhtälöön \(7x \equiv 2 \pmod{5}\).

Bezout’n lemmasta saadaankin seuraava tulos.

Lause 18.3 (Lineaariset kongruenssiyhtälöt) Oletetaan, että \(a\) ja \(b\) ovat yhteistekijättömiä positiivisia kokonaislukuja. Olkoon \(c\) jokin kokonaisluku. Tällöin yhtälöllä \[ax \equiv c \pmod{b}\] on tasan yksi ratkaisu modulo \(b\).

Todistus.

Ratkaisun olemassaolo: Bezout’n lemman nojalla on olemassa sellaiset kokonaisluvut \(x\) ja \(y\), että \(ax + by = c\). Ottamalla tämä yhtälö modulo \(b\) saadaan \(ax \equiv c \pmod{b}\).

Ratkaisun yksikäsitteisyys modulo \(b\): Oletetaan, että joillakin kahdella kokonaisluvulla \(x_1\) ja \(x_2\) pätee \(ax_1 \equiv c \pmod{b}\) ja \(ax_2 \equiv c \pmod{b}\). Tällöin \(ax_1 \equiv ax_2 \pmod{b}\), eli \[b \mid ax_1 - ax_2 = a(x_1 - x_2).\] Koska \(a\) ja \(b\) ovat yhteistekijättömiä, seuraa tästä \[b \mid x_1 - x_2\] (kuten nähdään miettimällä lukujen \(a, b\) ja \(x_1 - x_2\) alkutekijähajotelmia). Täten \[x_1 \equiv x_2 \pmod{b},\] mikä on haluttu väite.

18.6 Tehtäviä

Alkupään tehtävät eivät ole kovin soveltavia, vaan niiden on tarkoitus tukea tekstin aiheiden oppimista. Loppupäässä on hieman luovuutta vaativia tehtäviä.

Tehtävä 1.

Etsi kaikki kokonaisluvut \(x\) ja \(y\), joilla \(2x - 5y = 1\).
Etsi kaikki kokonaisluvut \(x\) ja \(y\), joilla \(3x + 6y = 3\).

Tehtävä 2. Etsi kaikki kokonaisluvut \(x\), jotka toteuttavat yhtälön

\(2x \equiv 1 \pmod{3}\)
\(3x \equiv 4 \pmod{10}\)
\(4x \equiv 2 \pmod{6}\).

Tehtävä 3. Olkoot \(a\) ja \(b\) positiivisia kokonaislukuja, joiden suurin yhteinen tekijä on \(d\). Osoita, että yhtälöllä \(ax + by = c\) on kokonaislukuratkaisu \(x, y\) täsmälleen silloin, kun \(c\) on jaollinen luvulla \(d\).

Tehtävä 4. Olkoon \(c\) mielivaltainen kokonaisluku. Osoita, että on olemassa kokonaisluvut \(x, y\) ja \(z\), joilla \[6x + 10y + 15z = c.\]

Tehtävä 5. Bezout’n lemman todistuksessa osoitettiin, että jos \(\text{syt}(a, b) = 1\), niin \(\text{syt}(a-b, b) = 1\). Osoita yleisemmin, että \(\text{syt}(a, b) = \text{syt}(a-b, b)\) millä tahansa positiivisilla kokonaisluvuilla \(a\) ja \(b\), joilla \(a > b\).

Tehtävä 6. Laske \(\text{syt}(10013, 11687)\) (ilman laskinta).

Tehtävä 7. Olkoon \(n\) positiivinen kokonaisluku. Osoita, että \(\syt(21n+4, 14n+3) = 1\).